506D Mr. Kitayuta's Colorful Graph (并查集+STL)

D. Mr. Kitayuta's Colorful Graph

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Mr. Kitayuta has just bought an undirected graph with n vertices and m edges. The vertices of the graph are numbered from 1 to n. Each edge, namely edge i, has a color c_i, connecting vertex a_i and b_i.

Mr. Kitayuta wants you to process the following q queries.

In the i-th query, he gives you two integers - u_i and v_i.

Find the number of the colors that satisfy the following condition: the edges of that color connect vertex u_i and vertex v_i directly or indirectly.

Input

The first line of the input contains space-separated two integers - n and m(2 ≤ n ≤ 10⁵, 1 ≤ m ≤ 10⁵), denoting the number of the vertices and the number of the edges, respectively.

The next m lines contain space-separated three integers - a_i, b_i(1 ≤ a_i < b_i ≤ n) and c_i(1 ≤ c_i ≤ m). Note that there can be multiple edges between two vertices. However, there are no multiple edges of the same color between two vertices, that is, if i ≠ j, (a_i, b_i, c_i) ≠ (a_j, b_j, c_j).

The next line contains a integer- q(1 ≤ q ≤ 10⁵), denoting the number of the queries.

Then follows q lines, containing space-separated two integers - u_i and v_i(1 ≤ u_i, v_i ≤ n). It is guaranteed that u_i ≠ v_i.

Output

For each query, print the answer in a separate line.

Sample test(s)

input

4 5
1 2 1
1 2 2
2 3 1
2 3 3
2 4 3
3
1 2
3 4
1 4

output

2
1
0

input

5 7
1 5 1
2 5 1
3 5 1
4 5 1
1 2 2
2 3 2
3 4 2
5
1 5
5 1
2 5
1 5
1 4

output

1
1
1
1
2

Note

Let's consider the first sample.

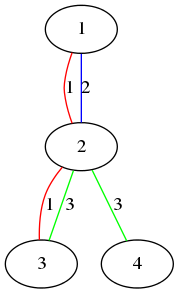The figure above shows the first sample.

• Vertex 1 and vertex 2 are connected by color 1 and 2.
• Vertex 3 and vertex 4 are connected by color 3.
• Vertex 1 and vertex 4 are not connected by any single color.

题意：有n个点和m条路,每条路都有固定的颜色,给你q次询问,问点u->v有几种走法,每次只能沿一种颜色走。

思路：根据数据的范围,用并查集,可将相同颜色道路所连得点合并,我自己写的代码比较搓,耗时也高,就贴一位大神的代码,其中的M我不知道为啥要分情况讨论,后来才知道妙处

代码：//436 ms  8500 KB

#include<cstdio>
#include<algorithm>
#include<vector>
#include<map>
#define N 100100
#define M 300
using namespace std;
int f[N],ans[N];
pair<int,int> q[N];
vector<pair<int,int> > col[N],total;
map<pair<int,int>,int> light;
int find(int x)
{
    if(f[x]==x) return x;
    return f[x]=find(f[x]);
}
void uni(int x,int y)
{
    if(find(x)==find(y)) return;
    f[find(x)]=find(y);
}
int main()
{
    int n,m,a,b,c,i,j,k,l;
    scanf("%d%d",&n,&m);
    for(i=0; i<m; i++)
    {
        scanf("%d%d%d",&a,&b,&c);
        col[c].push_back(make_pair(a,b));//col[c][i]中存着c颜色道路的a,b点信息
    }
    scanf("%d",&k);
    for(i=0; i<k; i++)
    {
        scanf("%d%d",&q[i].first,&q[i].second);
        if(q[i].first>q[i].second) swap(q[i].first,q[i].second);
        light[q[i]]=0;
    }
    for(i=1; i<=m; i++)
    {
        if(col[i].size()<M)//这里的分情况讨论能大大缩短一些样例的时间
        {
            vector<int> vertex;
            for(j=0; j<col[i].size(); j++)
            {
                vertex.push_back(col[i][j].first);
                vertex.push_back(col[i][j].second);
            }
            sort(vertex.begin(),vertex.end());//都先将同一颜色的点放入集合中,排序并去重用做查找,再用并查集合并道路两定点,最后计算
            vertex.resize(unique(vertex.begin(),vertex.end())-vertex.begin());
            for(j=0; j<vertex.size(); j++)
            {
                f[vertex[j]]=vertex[j];
            }
            for(j=0; j<col[i].size(); j++)
            {
                uni(col[i][j].first,col[i][j].second);
            }
            for(j=0; j<vertex.size(); j++)//这里的复杂度有O(n^n)所以点数不能太大
            {
                for(l=j+1; l<vertex.size(); l++)
                {
                    if(find(vertex[j])!=find(vertex[l])) continue;
                    if(light.count(make_pair(vertex[j],vertex[l])))
                    {
                        light[make_pair(vertex[j],vertex[l])]++;
                    }
                }
            }
        }
        else
        {
            for(j=1; j<=n; j++) f[j]=j;
            for(j=0; j<col[i].size(); j++)

            {
                uni(col[i][j].first,col[i][j].second);
            }
            for(j=0; j<k; j++)//这里复杂度就是max(O(n),O(k) ),而最大10^5,当集合顶点多时候可在k个q询问中寻找
            {
                if(find(q[j].first)==find(q[j].second)) ans[j]++;
            }
        }
    }
    for(i=0; i<k; i++)
    {
        printf("%d\n",light[q[i]]+ans[i]);
    }
    return 0;
}