ST表优化区间gcd

ST表的使用需要所求区间答案具有可重复性(询问时需要用到两个区间重叠来覆盖询问区间)
此题要求gcd为x的区间个数
可以用ST表处理出所有区间的\(gcd\) \(O(nlogn)\)

将区间的左端点\(l\)固定所有以 \(l\) 为左端点的区间\(gcd\)不超过\(log(n)\)个 及全部区间的\(gcd\)不超过\(nlogn\)种
证明：
以\(l\)为左端点\(r\)在向右扩的过程中此区间\((l,r)\)的\(gcd\)只会不变或减小(显然成立法)而每次减小必定是会少一个因子至少会除\(2\)所以最多也就\(log(n)\)个\(l\)的位置有\(n\)个所以所有区间就有\(nlogn\)种\(gcd\)

据此我们可以求出所有\(cnt[gcd_i]\)\((gcd\)为\(gcd_i\)的区间个数\()\)
当\(l\)固定时区间\(gcd\)的分布为一段一段的(\(gcd_1,gcd_2,gcd_3,...\))且具有二分性可以用二分找到\(gcd\)变化的位置从而求出\(gcd\)为\(gcd_i\)的区间个数累加到\(cnt[gcd_i]\)中

最后询问直接输出\(cnt[x]\)即可

CGCDSSQ

题面翻译

给出一个长度为\(n(1<=n<=10^{5})\) 的序列和\(q(1<=q<=3*10^{5})\) 个询问,每个询问输出一行,询问\(gcd(a_l,a_{l+1},...,a_r)=x\) 的\((i,j)\) 的对数.

感谢@凌幽 提供的翻译

题目描述

Given a sequence of integers $ a_{1},...,a_{n} $ and $ q $ queries $ x_{1},...,x_{q} $ on it. For each query $ x_{i} $ you have to count the number of pairs $ (l,r) $ such that $ 1<=l<=r<=n $ and $ gcd(a_{l},a_{l+1},...,a_{r})=x_{i} $ .

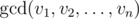is a greatest common divisor of $ v_{1},v_{2},...,v_{n} $ , that is equal to a largest positive integer that divides all $ v_{i} $ .

输入格式

Given a sequence of integers $ a_{1},...,a_{n} $ and $ q $ queries $ x_{1},...,x_{q} $ on it. For each query $ x_{i} $ you have to count the number of pairs $ (l,r) $ such that $ 1<=l<=r<=n $ and $ gcd(a_{l},a_{l+1},...,a_{r})=x_{i} $ .

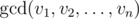is a greatest common divisor of $ v_{1},v_{2},...,v_{n} $ , that is equal to a largest positive integer that divides all $ v_{i} $ .

输出格式

For each query print the result in a separate line.

样例 #1

样例输入 #1

3
2 6 3
5
1
2
3
4
6

样例输出 #1

1
2
2
0
1

样例 #2

样例输入 #2

7
10 20 3 15 1000 60 16
10
1
2
3
4
5
6
10
20
60
1000

样例输出 #2

14
0
2
2
2
0
2
2
1
1

---

std

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define il inline 
#define re register
const int N = 1e5+9;
int n,m,f[N][25];
map<int,ll>cnt;
il int gcd(re int x,re int y)
{
	while(y)
	{
		x%=y;
		swap(x,y);
	}
	return x;
}

il init()
{
	for(re int j = 1;j <= 23;j++)
		for(re int i = 1;i+(1<<j)-1 <= n;i++)
			f[i][j] = gcd(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}

il int query(int l,int r)
{
	re int k = log2(r-l+1);
	return gcd(f[l][k],f[r-(1<<k)+1][k]);
}

int main()
{
	scanf("%d",&n);
	for(re int i = 1;i <= n;i++)scanf("%d",&f[i][0]);
	init();
	for(re int i = 1;i <= n;i++)
	{
		re int L = i;
		while(L <= n)
		{
			
			re int st = query(i,L);
			int l = L,r = n+1;
			while(l < r)
			{
				int mid = (l+r)>>1;
				if(query(i,mid) != st)r = mid;
				else l = mid+1;
			}
			
			cnt[st] += l-L;
			L = l;	
		}
	}
	
	scanf("%d",&m);
	while(m--)
	{
		re int x;
		scanf("%d",&x);
		printf("%lld\n",cnt[x]);
	}
	
	return 0;
}