利用质因数分解定理求与n互质的数的个数

今天我来分享一下如何利用素数分解定理求解与n互质的数的个数。

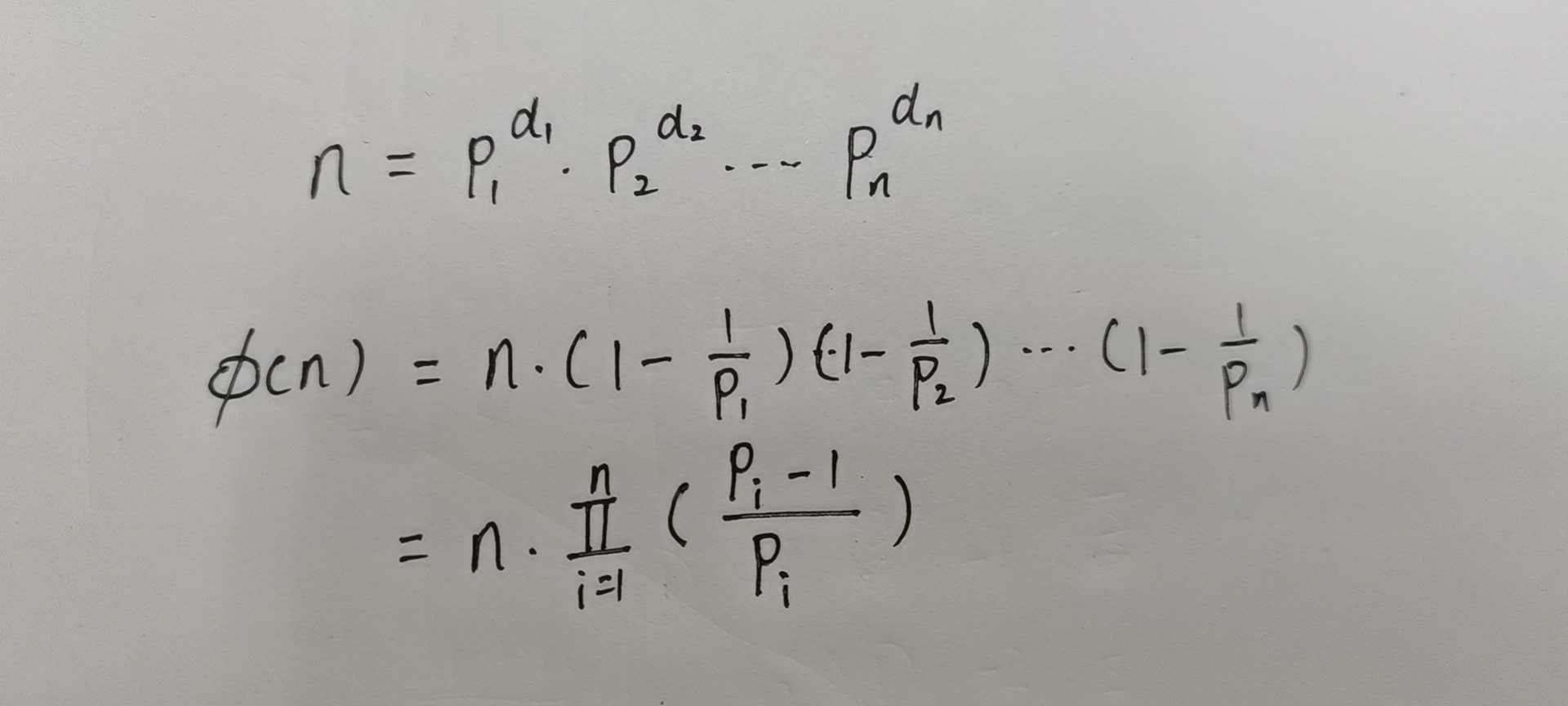
下面是代码

#include<bits/stdc++.h>
using namespace std;
long long fun(int x)
{
	long long ans=x;
	int t=sqrt(x);
	int cnt;
	for(int i=2;i<=t;i++)
	{
		cnt=0;
		while(x%i==0)
		{
			x/=i;
			cnt++;
		}
		if(cnt) ans=ans*(i-1)/i;
	}
	if(x>1) ans=ans*(x-1)/x;
	return ans;
}
int main()
{
	int n;
	cin>>n;
	int t;
	while(n--)
	{
		cin>>t;
		printf("%lld\n",fun(t));
	}
	return 0;
}

　　如果要求解1~n中的所有欧拉函数的和的话，那么一个一个地来求就显得不那么方便了，这时候我们可以利用线性筛法来求

#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N=1000010;
int prime[N], cnt;
int euler[N];
bool vis[N];
void get_eulers(int n)
{
    euler[1]=1;
    for(int i=2;i<=n;i++)
    {
        if (!vis[i])
        {
            prime[cnt++]=i;
            euler[i]=i-1; 
        }
        for (int j = 0; prime[j] <= n / i; j++)
        {
            vis[prime[j]*i]=true;
            if(i%prime[j]==0)
            {
                euler[prime[j]*i]=euler[i]*prime[j]; 
                break;
            }
            euler[prime[j]*i]=euler[i]*(prime[j]-1);
        }
    }
}
int main()
{
    int n;
    cin>>n;
    get_eulers(n);
    LL res=0;
    for(int i=1;i<=n;i++) res+=euler[i];
    printf("%lld\n",res);
    return 0;
}

　　代码解释：