单调栈
刚学完单调栈,就想来跟大家分享一下我对单调栈的理解
所谓单调栈,顾名思义,就是元素具有单调性的一个栈。今天我就来分享下他的一个用处(可以用来求一行元素中左边/右边第一个比他大/小的元素的位置);
我们如何来维护一个单调递增栈呢?
举个例子 3,8,9,6,7,2
开始时栈为空,我们把3放入栈中,下一个考虑元素8,此时栈顶元素是3,8大于3,我们就可以把8放入栈中,此时栈中元素为3,8;至于9呢?他大于8,当然是放在8的后面了,现在栈中元素为3,8,9;接下来到6了,但是此时栈顶元素是9,6<9,我们不能直接把6放入栈中,我们可以把9pop出栈,那么此时栈顶元素为8,依旧大于6,那么我们把8也pop出栈,此时栈顶元素就为3了,3<6,我们把6放入栈中,此时栈中元素为3,6;7呢?7>6当然是直接放入栈中啦,此时栈中元素为3,6,7;最后一个元素为2,我们发现7>2,6>2,3>2,我们只能把所有的元素都pop出栈,最后把2放进去,到这,一个模拟构造单调栈的过程就算是完成了。
3 --> 3 8 --> 3 8 9 -->3 6 -->3 6 7 -->2
说到这了,那单调递增栈到底有什么用呢?不知道大家有没有发现,栈中每个元素的左边都是第一个比他小的元素,例如8的左边是3,在原来序列中3是在8左边的第一个比8小的数,同理6也一样,那右边第一个比他小的呢,我们考虑6进栈时的情况,为了维护单调递增栈,是不是8和9两个元素被pop出去了,那6是不是就是8和9两个元素右边的第一个比他们小的元素,因为若有比8和9小的元素且在6的前面,那8和9一定会被pop出去的,对吧!这意味着一个元素的右边第一个比他小的元素是在这个元素出栈时被找到的,那会不会最后栈里面还有剩余没有被pop出去的元素呢?那这是不是意味着这些元素右边第一小的元素无法被找到呢?当然不是啦,我们考虑一下,他们为什么会留在栈中,如果他们遇到了在他们右边且比他们小的元素,他们还会在栈中么?所以说之所以栈中会出现剩余元素,那是因为他们右边没有比他们更小的元素,那我们是不是应该把他们的右边第一小元素的位置赋值为这一行的右边界呢。总的来说,我们从1遍历到n即可找到每个元素左边以及右边第一个比他小的元素,这种方法的复杂度是o(n)的。
上面我们说到单调递增栈可以用来求一个元素左边第一个比他小和右边第一个比它小的元素,那单调递减栈呢?是不是可以用来求一个元素左边第一个比他大和右边第一个比它大的元素呢?答案是肯定的,至于原理么,与递增栈是一样的,我就不多做赘述了。
下面来看一个例题吧。
题目介绍:直方图是由在公共基线上对齐的一系列矩形组成的多边形。矩形的宽度相等,但可能有不同的高度。例如,左边的图显示由高度为2、1、4、5、1、3、3的矩形组成的直方图,单位为1是矩形的宽度:
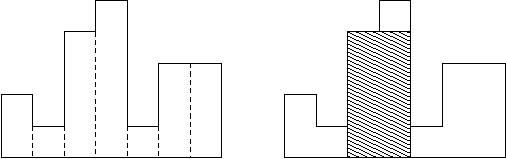
通常,直方图用于表示离散分布,例如文本中字符的频率。请注意,矩形的顺序,即它们的高度,是很重要的。计算直方图中在公共基线上对齐的最大矩形的面积。右边的图显示了所描述的直方图的最大对齐矩形。
输入包含几个测试用例。每个测试用例描述一个直方图,从一个整数n开始,表示由它组成的矩形的数目。你可以假设1<=n<=100000。然后跟着n个整数H1,.,hn,其中0<=hi<=1000000000。这些数字表示从左到右的直方图矩形的高度.每个矩形的宽度为1,最后一次测试用例的输入为零。
对于单行上的每个测试用例输出,指定直方图中最大矩形的面积。请记住,此矩形必须在公共基线处对齐。
样例
输入7 2 1 4 5 1 3 3
4 1000 1000 1000 1000 0
输出
8
4000
我们来分析一下这道题:通过样例分析不难发现答案所求的矩形中一定包含一个一个宽度为1且高度恰好为所求矩形高度的矩形(仔细理解一下这句话,很有用)。
我们假设所求答案是由第i个宽度为1的矩形扩展而来的,要想能够扩展,那么在这个矩形里面所有宽度为1的矩形的高度是不是都要比第i个矩形高,那么左边界是不是第i个矩形左边第一个比他低的
矩形的位置,而右边界是第i个矩形右边第一个比他低的矩形的位置,那么问题就转换为一个单调栈问题了,我们只需要维护一个单调递增栈,最后遍历一边最大值即可,下面是代码
、、、
#include<stdio.h>
#include<stack>
using namespace std;
long long a[100002];
long long l[100002],r[100002];
int main()
{
int n;
stack<int>p;
while(scanf("%lld",&n))
{
if(n==0) break;
for(int i=1;i<=n;i++)
scanf("%lld",&a[i]);
for(int i=1;i<=n;i++)
{
while(p.size()&&(a[p.top()]>=a[i]))//此处一定要保证栈内有元素的情况下再比较
{
r[p.top()]=i;//元素出栈时更新出栈元素的右边界
p.pop();
}
if(!p.empty())
l[i]=p.top();//更新刚入栈元素的左边界
else l[i]=0;//栈为空时更新入栈元素左边界为0
p.push(i);
}
while(!p.empty())
{
r[p.top()]=n+1;//将栈内剩余元素的有边界更新为所读入元素的最右位置+1
p.pop();
}
long long ans=0;
for(int i=1;i<=n;i++)
ans=max(ans,(r[i]-l[i]-1)*a[i]);//每次更新一次以第i个矩形作为答案矩形的最大值
printf("%lld\n",ans);
}
return 0;
}
注意:此处做下修改,上面思路有个隐形错误,我当时没发现,现在给读者作下提醒:如果元素中存在相同的元素,则用上述方法求右边第一小的元素时就会出问题,仔细想下为什么?
下面给出一个万能的方法:上面求左边第一小元素时是没有问题的,我们可以利用类似的思路来求右边第一小的元素,那就是将数组倒序遍历,这样不就能求出右边第一小的元素了么?
下面给出代码,希望读者好好体会!
#include<iostream> #include<string> #include<cstdio> #include<stack> using namespace std; const int N=100002; typedef long long LL; LL h[N],l[N],r[N]; typedef pair<int,int> PII; stack<PII> ans; int main() { int n; while(1) { cin>>n; while(!ans.empty()) ans.pop();//多组输入时一定不要忘了清空原数组 if(n==0) return 0; for(int i=1;i<=n;i++) scanf("%lld",&h[i]); for(int i=1;i<=n;i++) { while(ans.size()&&(ans.top().first>=h[i])) ans.pop(); if(ans.empty()) l[i]=0; else l[i]=ans.top().second; ans.push(make_pair(h[i],i)); } while(!ans.empty()) ans.pop();//由于再求左边第一个小于他的元素时被赋值,故此处应清空 for(int i=n;i>=1;i--)//注意我们求右边第一小元素时要倒序遍历 { while(ans.size()&&(ans.top().first>=h[i])) ans.pop(); if(ans.empty()) r[i]=n+1; else r[i]=ans.top().second; ans.push(make_pair(h[i],i)); } LL ans=0; for(int i=1;i<=n;i++) ans=max(ans,h[i]*(r[i]-l[i]-1)); printf("%lld\n",ans); } return 0; }
至于第一个错误的思路及代码我就不删了,也希望大家能够认识到这个陷阱,啊啊啊啊啊啊,博主怎么都不会想到有一天会在做题时发现这个错误并debug了半天才明白,希望大家能够少走这个弯路!
下面我给出一个进阶版的求矩形面积的题:
有一天,小猫 rainbow 和 freda 来到了湘西张家界的天门山玉蟾宫,玉蟾宫宫主蓝兔盛情地款待了它们,并赐予它们一片土地。
这片土地被分成 N×M 个格子,每个格子里写着 R 或者 F,R 代表这块土地被赐予了 rainbow,F 代表这块土地被赐予了 freda。
现在 freda 要在这里卖萌。。。它要找一块矩形土地,要求这片土地都标着 F 并且面积最大。
但是 rainbow 和 freda 的 OI 水平都弱爆了,找不出这块土地,而蓝兔也想看 freda 卖萌(她显然是不会编程的……),所以它们决定,如果你找到的土地面积为 SS,它们将给你 3×S3×S 两银子。
输入格式
第一行包括两个整数 N,M,表示矩形土地有 N 行 M 列。
接下来 N 行,每行 M 个用空格隔开的字符 F 或 R,描述了矩形土地。
每行末尾没有多余空格。
输出格式
输出一个整数,表示你能得到多少银子,即(3×3×最大 F 矩形土地面积)的值。
数据范围
1≤N,M≤1000
输入样例:
5 6
R F F F F F
F F F F F F
R R R F F F
F F F F F F
F F F F F F
输出样例:
45
这道题与矩形面积就比较类似了,我们可以把每一行的最大值都求一遍,最后再取一个最大值就好了
但是注意这道题的输入格式里面包含大量的空格,所以建议用cin读入,可以自动去掉空格
下面给出两种代码,第一种使用了stl库里面的栈,第二种是数组模拟的栈,建议使用第二种,调用stl库里面的栈会比较慢,容易卡时间
//使用stl库里面容器 (有时会被卡时间) #include<iostream> #include<string> #include<cstdio> #include<stack> using namespace std; const int N=1002; typedef long long LL; typedef pair<int,int> PII; stack<PII> ans; LL s[N][N],l[N],r[N]; int main() { int n,m; cin>>n>>m; char c; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) { cin>>c; if(c=='F') s[i][j]=s[i-1][j]+1; else s[i][j]=0; } LL anss=0; for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { while(!ans.empty()&&(ans.top().first>=s[i][j])) ans.pop(); if(ans.empty()) l[j]=0; else l[j]=ans.top().second; ans.push(make_pair(s[i][j],j)); } while(!ans.empty()) ans.pop(); for(int j=m;j>=1;j--) { while(!ans.empty()&&(ans.top().first>=s[i][j])) ans.pop(); if(ans.empty()) r[j]=m+1; else r[j]=ans.top().second; ans.push(make_pair(s[i][j],j)); } for(int j=1;j<=m;j++) anss=max(anss,s[i][j]*(r[j]-l[j]-1)); } printf("%lld",3*anss); return 0; } //数组模拟栈 #include<iostream> #include<string> #include<cstdio> #include<stack> using namespace std; const int N=1002; typedef long long LL; typedef pair<int,int> PII; int ans[N],tt; LL s[N][N],l[N],r[N]; int main() { int n,m; scanf("%d%d",&n,&m); char c; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) { cin>>c; if(c=='F') s[i][j]=s[i-1][j]+1; else s[i][j]=0; } LL anss=0; for(int i=1;i<=n;i++) { tt=0; for(int j=1;j<=m;j++) { while(tt&&(s[i][ans[tt]]>=s[i][j])) tt--; if(!tt) l[j]=0; else l[j]=ans[tt]; ans[++tt]=j; } tt=0; for(int j=m;j>=1;j--) { while(tt&&(s[i][ans[tt]]>=s[i][j])) tt--; if(!tt) r[j]=m+1; else r[j]=ans[tt]; ans[++tt]=j; } for(int j=1;j<=m;j++) anss=max(anss,s[i][j]*(r[j]-l[j]-1)); } printf("%lld",3*anss); return 0; }
最后再给出一道更有意思的单调栈的题
给定一个 N×M 的 0101 矩阵,矩阵下标从 0 开始。
有 Q 个询问,第 i 个询问为:将矩阵中 (xi,yi) 的元素改成 0 之后,只包含 1 的子矩阵的最大面积是多少。
注意:
- 每次询问均是独立的。
- 询问方格内元素可能本来就是 0。
- 子矩阵的面积是指矩阵的大小。
输入格式
第一行包含两个整数 N,M。
接下来 N 行,每行包含 M 个 01 字符。
再一行包含整数 Q。
接下来 Q 行,每行包含 2 个整数 (xi,yi)。
输出格式
每个询问输出一行一个结果,表示最大面积。
数据范围
对于 20% 的数据,1≤N,M,Q≤10
对于 50% 的数据,1≤N,M,Q≤100
对于 100% 的数据,1≤N,M≤2000,1≤Q≤105 0≤xi<n,0≤yi<m
输入样例:
4 2
10
11
11
11
3
0 0
2 0
3 1
输出样例:
6
3
4
分析这道题就会发现,这道题比前两题更难处理一些,因为他去掉的位置是随机的,所以显然需要预处理出来一些东西,那应该预处理出来什么呢?
仔细分析我们就可以发现,答案矩阵一定在所去除方格的上方或者下方或者左方或者右方,他一定可以被一个方向上的区间涵盖,画个图应该就知道为什么了
那我们现在就要预处理出来每一个方格四个方向上符合题意的最大的矩形面积
至于上方么,这个和第一道例题是类似的,处理下方时,我们应该将矩形旋转180度当作上方的矩形来处理,左方和右方的矩形就需要旋转90度,也当作朝上的矩形来看待;
说起来比较容易,可真正理解起来并没有那么简单,博主也是理解了好长时间才明白的,不过对于大家的思维提升真的有帮助,希望大家能够好好理解!
下面我给出代码:
//直接调用stl库里面的栈 (有时会被卡时间) #include<iostream> #include<cstdio> #include<stack> #include<cstring> using namespace std; const int N=2002; typedef pair<int,int> PII; int U[N],D[N],L[N],R[N]; int l[N],r[N]; char a[N][N]; int s[N][N]; int n,m; stack<PII> ans; //calc函数求的是以以它为底边的最大矩形面积 int calc(int h[],int n)//n为数组长度 { while(!ans.empty()) ans.pop(); for(int i=1;i<=n;i++) { while(!ans.empty()&&ans.top().first>=h[i]) ans.pop(); if(ans.empty()) l[i]=0; else l[i]=ans.top().second; ans.push(make_pair(h[i],i)); } while(!ans.empty()) ans.pop(); for(int i=n;i>=1;i--) { while(!ans.empty()&&ans.top().first>=h[i]) ans.pop(); if(ans.empty()) r[i]=n+1; else r[i]=ans.top().second; ans.push(make_pair(h[i],i)); } int ans=0; for(int i=1;i<=n;i++) ans=max(ans,h[i]*(r[i]-l[i]-1)); return ans; } void init() { for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) if(a[i][j]=='1') s[i][j]=s[i-1][j]+1; else s[i][j]=0; U[i]=max(U[i-1],calc(s[i],m)); } memset(s,0,sizeof(s)); for(int i=n;i>=1;i--)//以i为底边 { for(int j=1;j<=m;j++) if(a[i][j]=='1') s[i][j]=s[i+1][j]+1; else s[i][j]=0; D[i]=max(D[i+1],calc(s[i],m)); } memset(s,0,sizeof(s)); //求l和r数组时,以列作为矩形底边,将矩形旋转90度 for(int i=1;i<=m;i++) { for(int j=1;j<=n;j++) if(a[j][i]=='1') s[i][j]=s[i-1][j]+1;//这里写成s[i][j]的原因是直接将数组转置,将求第i列转换为求第i行 else s[i][j]=0; L[i]=max(L[i-1],calc(s[i],n)); } memset(s,0,sizeof(s)); for(int i=m;i>=1;i--) { for(int j=1;j<=n;j++) if(a[j][i]=='1') s[i][j]=s[i+1][j]+1; else s[i][j]=0; R[i]=max(R[i+1],calc(s[i],n)); } } int main() { cin>>n>>m; for(int i=1;i<=n;i++) scanf("%s",a[i]+1); int x,y; init(); int q; cin>>q; while(q--) { cin>>x>>y; x++;y++;//注意数组下标 printf("%d\n",max(max(U[x-1],D[x+1]),max(L[y-1],R[y+1]))); } return 0; } //数组模拟栈 #include<iostream> #include<cstdio> #include<stack> #include<cstring> using namespace std; const int N=2002; int U[N],D[N],L[N],R[N]; int l[N],r[N]; char a[N][N]; int s[N][N]; int n,m; int ans[N],tt; //calc函数求的是以以它为底边的最大矩形面积 int calc(int h[],int n)//n为数组长度 { tt=0; for(int i=1;i<=n;i++) { while(tt&&h[ans[tt]]>=h[i]) tt--; if(!tt) l[i]=0; else l[i]=ans[tt]; ans[++tt]=i; } tt=0; for(int i=n;i>=1;i--) { while(tt&&h[ans[tt]]>=h[i]) tt--; if(!tt) r[i]=n+1; else r[i]=ans[tt]; ans[++tt]=i; } int ans=0; for(int i=1;i<=n;i++) ans=max(ans,h[i]*(r[i]-l[i]-1)); return ans; } void init() { for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) if(a[i][j]=='1') s[i][j]=s[i-1][j]+1; else s[i][j]=0; U[i]=max(U[i-1],calc(s[i],m)); } memset(s,0,sizeof(s)); for(int i=n;i>=1;i--)//以i为底边 { for(int j=1;j<=m;j++) if(a[i][j]=='1') s[i][j]=s[i+1][j]+1; else s[i][j]=0; D[i]=max(D[i+1],calc(s[i],m)); } memset(s,0,sizeof(s)); //求l和r数组时,以列作为矩形底边,将矩形旋转90度 for(int i=1;i<=m;i++) { for(int j=1;j<=n;j++) if(a[j][i]=='1') s[i][j]=s[i-1][j]+1;//这里写成s[i][j]的原因是直接将数组转置,将求第i列转换为求第i行 else s[i][j]=0; L[i]=max(L[i-1],calc(s[i],n)); } memset(s,0,sizeof(s)); for(int i=m;i>=1;i--) { for(int j=1;j<=n;j++) if(a[j][i]=='1') s[i][j]=s[i+1][j]+1; else s[i][j]=0; R[i]=max(R[i+1],calc(s[i],n)); } } int main() { cin>>n>>m; for(int i=1;i<=n;i++) scanf("%s",a[i]+1); int x,y; init(); int q; cin>>q; while(q--) { cin>>x>>y; x++;y++;//注意数组下标 printf("%d\n",max(max(U[x-1],D[x+1]),max(L[y-1],R[y+1]))); } return 0; }
好了,以上就是我对单调栈的一些理解了,如果里面有错误,请记得提醒博主哈,感谢大家的阅读!

 浙公网安备 33010602011771号
浙公网安备 33010602011771号