集合基础

集合基础

集合接口：

Set

• void add(E) //该方法不能添加重复元素
• void remove(E)
• boolean contains(E)
• int getSize()
• boolean isEmpty()

接口代码的编写大概是这样:

public interface Set {
    void add(int i);
    void remove(int i);
    boolean contains(int i);
    int getSize();
    boolean isEmpty();
}

使用二分搜索树实现集合：

我实现的二分搜索树只能存储int类型的数据，如果你想要能存储其他数据，就需要用到泛型，因为二分搜索树所存储的元素都具有可比较性，所以泛型需要继承Comparable接口

public class BSTSet implements Set {

    private BST bst;

    public BSTSet(){
        bst = new BST();
    }

    @Override
    public void add(int i) {
        bst.insert(i);
    }

    @Override
    public void remove(int i) {
        bst.remove(i);
    }

    @Override
    public boolean contains(int i) {
        return bst.lookup(i);
    }

    @Override
    public int getSize() {
        return bst.getSize();
    }

    @Override
    public boolean isEmpty() {
        return bst.getSize()==0;
    }
}

使用链表实现集合：

	package LinkedListSet;
	
	import java.util.LinkedList;
	
	public class LinkedListSet implements Set {

    private LinkedList list;

    public LinkedListSet(){
        list = new LinkedList();
    }

    @Override
    public void add(int i) {
        if (!list.contains(i))
            list.addFirst(i);
    }

    @Override
    public void remove(int i) {
        list.remove(i);
    }

    @Override
    public boolean contains(int i) {
        return list.contains(i);
    }

    @Override
    public int getSize() {
        return list.size();
    }

    @Override
    public boolean isEmpty() {
        return list.isEmpty();
    }
}

使用链表实现集合十分简单，主要的区别是在add时要多一步判断，而二分搜索树就不需要

简单分析下时间复杂度：

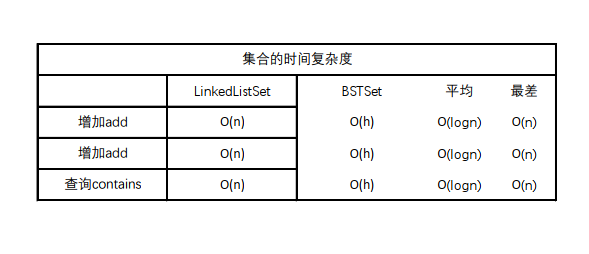
h指的是树的高度，h与n的关系是:

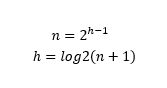
最差的情况指的是二分搜索树退化成链表(以顺序的或者接近顺序的输入数据来创建树)，所以复杂度和链表一样。