网络流

1. 基本概念
    1.1 流网络，不考虑反向边
    1.2 可行流，不考虑反向边
        1.2.1 两个条件：容量限制、流量守恒
        1.2.2 可行流的流量指从源点流出的流量 - 流入源点的流量
        1.2.3 最大流是指最大可行流
    1.3 残留网络，考虑反向边，残留网络的可行流f' + 原图的可行流f = 原题的另一个可行流
        (1) |f' + f| = |f'| + |f|
        (2) |f'| 可能是负数
    1.4 增广路径
    1.5 割
        1.5.1 割的定义
        1.5.2 割的容量，不考虑反向边，“最小割”是指容量最小的割。
        1.5.3 割的流量，考虑反向边，f(S, T) <= c(S, T)
        1.5.4 对于任意可行流f，任意割[S, T]，|f| = f(S, T)
        1.5.5 对于任意可行流f，任意割[S, T]，|f| <= c(S, T)
        1.5.6 最大流最小割定理
            (1) 可行流f是最大流
            (2) 可行流f的残留网络中不存在增广路
            (3) 存在某个割[S, T]，|f| = c(S, T)
    1.6. 算法
        1.6.1 EK O(nm^2)
        1.6.2 Dinic O(n^2m)
    1.7 应用
        1.7.1 二分图
            (1) 二分图匹配
            (2) 二分图多重匹配
        1.7.2 上下界网络流
            (1) 无源汇上下界可行流
            (2) 有源汇上下界最大流
            (3) 有源汇上下界最小流
        1.7.3 多源汇最大流

基本概念

流网络

定义:一个有边权的有向图 G={V,E,s,t,c} V是所有的点集,E是所有的边集,s是源点,t为汇点,c为边权
我们可以把流网络类比成下水道,每一条边都相当于一根水管,每一根水管都有一个容量,即边权,
源点即为入水口,汇点即为排水口,并且在流网络中,我们不考虑反向边.
下面给出一个流网络例子

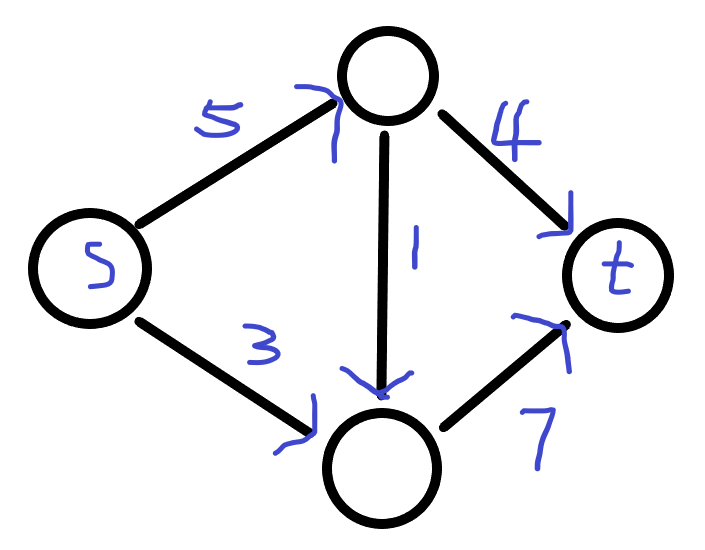
可行流

条件:流量守恒,容量限制.
对于每一个可行流,它在流网络中的每一条边的流量都不能大于容量限制,并且可行流的流量指源点流出的流量 - 流入源点的流量,最大流指的即是最大可行流
下面给出一个上面例子的一个可行流

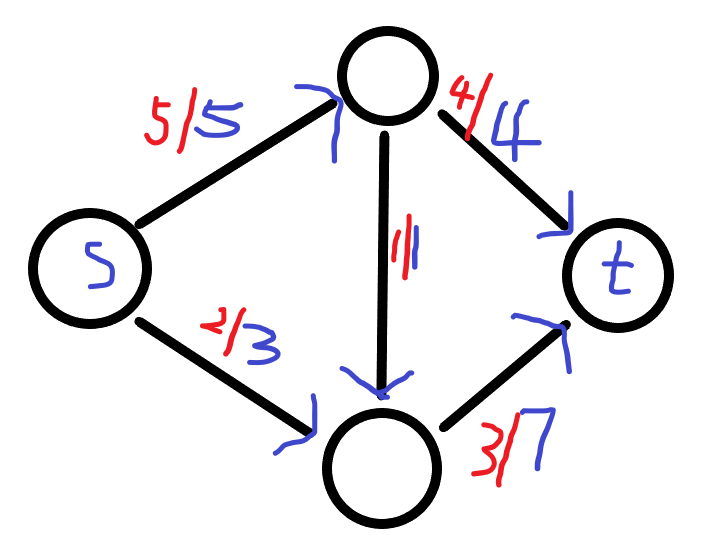
这个可行流的流量即为\(|f|=7\)

残留网络

残留网络是在可行流的基础上产生的,即每一个可行流对应一个残留网络,在残留网络中我们需要考虑反向边,
需要注意的是,残留网络也是一个流网络,那么它同样也满足流网络的定义,只不过需要考虑反向边,
我们定义该流网络中的边集为V,那么对于每一条残留网络的边它的容量
\(c'(u,v)= \begin{cases} c(u,v)-f(u,v), (u,v)\in{V} \\ f(v,u),(v,u)\in{V} \end{cases}\)
对于残留网络中的可行流,记作f'
对于一个残留网络,我们有f'+f也是一个原流网络的可行流
对于证明,我们可以考虑可行流的两个条件
对于流量守恒,可以感性理解下,显然成立
对于容量限制,我们讨论同向与反向,对于同向,即两条边的流量相加,对于反向,即两条边的流量相减
那么考虑两种情况
\(1^{。}\)同向
\(\because 0 \le f'(u,v) \le c'(u,v)=c(u,v)-f(u,v)\)
\(\therefore 0 \le f'(u,v)+f(u,v) \le c(u,v)\)
成立
\(2^{。}\)反向
\(\because 0 \le f'(u,v) \le c'(u,v)=f(v,u) \le c(v,u)\)
\(\therefore 0 \le f'(u,v) - f(v,u) \le c(v,u)\)
成立
那么就可以得到|f'+f|=|f'|+|f|

增广路径

对于一个可行流的残留网络,如果存在一条路径上所有的边的流量都大于0的s到t的路径,
那么我们就称这条路径为增广路径,很显然,如果有增广路径,那么这个可行流一定不是最大流
那如果一个可行流没有增广路径,能否说它一定是最大流?
这时候,我们就要引入割了

割

对于一个流网络的点集V,我们将它分为S,T两个集合,其中S,T满足\(s\in S,t \in T,S \cup T=V,S \cap T = \varnothing\)

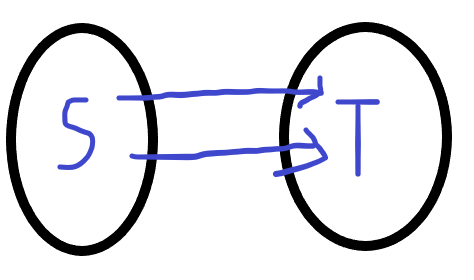
这就是一个割,对于一个割的容量,我们定义为\(c(S,T)=\sum\limits_{u \in S} \sum\limits_{v \in T} c(u,v)\)
割的流量,定义为\(f(S,T)=\sum\limits_{u \in S} \sum\limits_{v \in T} f(u,v)-\sum\limits_{v \in S} \sum\limits_{u \in T} c(v,u)\)
那么我们可以得到\(f(u,v)=-f(v,u),f(x,y \cup z)=f(x,z)+f(x,y),f(x,x)=0,f(x \cup y,z)=f(x,z)+f(y,z)\)
证明|f|=f(S,T)
\(\because f(S,T)+f(S,S)=f(S,V)\)
\(\therefore f(S,T)=f(S,V)-f(S,S)=f(S,V)=f(s,V)+f(S-{s},V)\)
令S'=S-{s}
\(\because f(S',V)= \sum\limits_{u \in S'} (\sum\limits_{v \in V} f(u,v)-\sum\limits_{v \in V} f(v,u))=0\)
\(\therefore f(S,T)=|f|\)
得证
明显我们可以的到\(f(S,T) \le \sum\limits_{u \in S} \sum\limits_{v \in T} c(u,v)-\sum\limits_{v \in S} \sum\limits_{u \in T} c(v,u) \le c(S,T)\)
即\(f(S,T) \le c(S,T)\)
我们就可以得到最大流小于最小割
有了割我们可以干什么,接下来就有了最大流最小割定理
(1) 可行流f是最大流
(2) 可行流f的残留网络中不存在增广路
(3) 存在某个割(S,T)，|f| = c(S, T)
其中知道任意一条,即可求出其他两条
证明
对于\((1)\Rightarrow (2)\)
我们可以用反证法,假设f为最大流,若它存在增广路,则它一定不是最大流,矛盾.
故若f为最大流,那么它一定不存在增广路
对于\((3) \Rightarrow (1)\)
\(\because 最大流 \le c(S,T)\)
又\(\because |f|=c(S,T)\)
\(\therefore 最大流 \le |f|\)
又\(\because |f| \le 最大流\)
\(\therefore |f|=最大流\)
对于\((2) \Rightarrow (3)\)
我们假设S为残留网络从s出发,沿流量大于0的边走,能够到达的点击,T=V-S

对于一条从S流向T的边(x,y),则f(x,y)=c(x,y),f(y,x)=0
若f(x,y)<c(x,y),那么在残留网络中,y就能被x遍历到,那么应该被划分到S中,故f(x,y)=c(x,y)
若f(y,x)>0,那么在残留网络中,就会有一条流量大于0的反向边使得y能被x遍历到,故f(y,x)=0;
得证
那么我们就得到了一个结论,如果一个可行流的残留网络中没有增广路径,那么它就是最大流

最大流

方法FF

while()
找增广路
更新残留网络

实现FF的两种方法
EK求最大流\(O(nm^2)\)

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N = 1005, M = 2e4 + 5, INF = 1e9;

int head[N], ver[M], c[M], net[M], f[M];
int tot, pre[N], q[N], n, m, S, T, vis[N];
    
void add(int a, int b, int w)
{
    ver[tot] = b, c[tot] = w, net[tot] = head[a], head[a] = tot++;
}

bool bfs()
{
    int front = 0, tail = -1;
    memset(vis, false, sizeof(vis));
    vis[S] = true, f[S] = INF, q[++tail] = S;
    while (front <= tail)
    {
        int u = q[front++];
        for (int i = head[u]; i; i = net[i])
        {
            int v = ver[i];
            if (!vis[v] && c[i])
            {
                vis[v] = true;
                f[v] = min(f[u], c[i]);
                pre[v] = i;
                if (v == T)
                    return true;
                q[++tail] = v;
            }
        }
    }
    return false;
}

long long EK()
{
    long long res = 0;
    while (bfs())
    {
        res += f[T];
        for (int i = T; i != S; i = ver[pre[i] ^ 1])
            c[pre[i]] -= f[T], c[pre[i] ^ 1] += f[T];
    }
    return res;
}

int main()
{
    scanf("%d%d%d%d", &n, &m, &S, &T);
    while (m--)
    {
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        add(u, v, w), add(v, u, 0);
    }
    printf("%lld", EK());
    return 0;
}

dinic求最大流\(O(n^2m)\)
主要是对EK算法进行了一些优化

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
const int N = 1e4 + 5, M = 2e5 + 5, INF = 1e9;

int n, m, S, T;
int head[N], net[M], cpt[M], ver[M],idx;
int f[N], cur[N], d[N], q[N];

void add(int a, int b, int c)
{
    net[idx] = head[a];
    ver[idx] = b;
    cpt[idx] = c;
    head[a] = idx++;
}

bool bfs()
{
    int front = 0, tail = 0;
    memset(d, -1, sizeof(d));
    q[0] = S, d[S] = 0, cur[S] = head[S];
    while (front <= tail)
    {
        int u = q[front++];
        for (int i = head[u]; ~i; i = net[i])
        {
            int v = ver[i];
            if (d[v] == -1 && cpt[i])
            {
                d[v] = d[u] + 1;
                f[v] = min(f[u], cpt[i]);
                cur[v] = head[v];
                if (v == T)
                    return true;
                q[++tail] = v;
            }
        }
    }
    return false;
}

int find(int u, int limit)
{
    if (u == T)
        return limit;
    int flow = 0;
    for (int i = cur[u]; ~i && flow < limit; i = net[i])
    {
        cur[u] = i;
        int v = ver[i];
        if (d[v] == d[u] + 1 && cpt[i])
        {
            int x = find(v, min(limit - flow, cpt[i]));
            if (!x)
                d[v] = -1;
            cpt[i] -= x, cpt[i ^ 1] += x, flow += x;
        }
    }
    return flow;
}

int dinic()
{
    int res = 0, flow;
    while (bfs())
    {
        while (flow = find(S, INF))
            res += flow;
    }
    return res;
}

int main()
{
    scanf("%d%d%d%d", &n, &m, &S, &T);
    memset(head, -1, sizeof(head));
    while (m--)
    {
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        add(u, v, w), add(v, u, 0);
    }
    printf("%d", dinic());
    return 0;
}

应用

二分图匹配

例题P2756 飞行员配对方案问题
这道可用之前学过的O(nm)算法匈牙利算法过掉，但是我们现在可用\(O(m \sqrt(n))\)的网络流来做这道题
首先考虑如何建图,先把源点和汇点建出,然后把外籍飞行员和英国飞行员分为两块

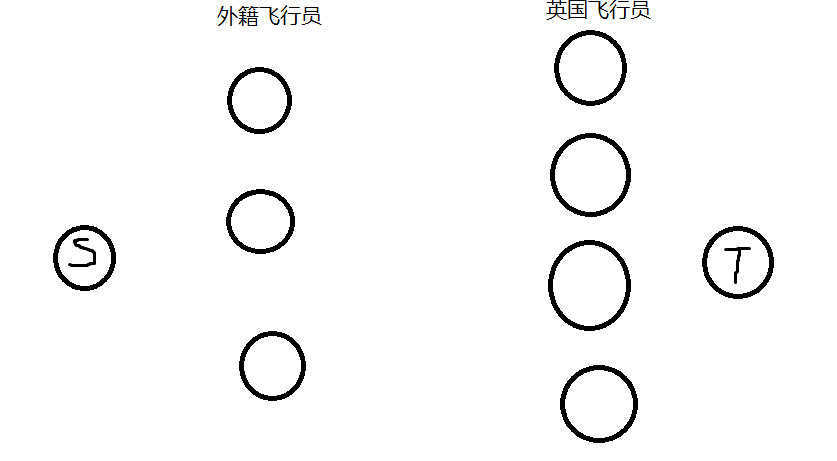
然后考虑如何连边,因为每个外籍飞行员只能连一个英国飞行员,所以考虑连给外籍飞行员与英国飞行员之间连一条容量为1的边,源点与汇点连向二分图的两部分,每条边的容量为1,
那么很明显,这是一个流网络,并且该流网络的最大流即为题目所求
代码

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N = 105, M = 5205, INF = 1e8;

int n, m, S, T;
int head[N], ver[M], net[M], cpt[M], idx;
int q[N], cur[N], d[N], f[N], front, tail;

void add(int a, int b , int c)
{
    net[idx] = head[a], ver[idx] = b, cpt[idx] = c, head[a] = idx++;
}

bool bfs()
{
    front = 0, tail = 0;
    memset(d, -1, sizeof(d));
    q[0] = S, d[S] = 0, cur[S] = head[S];
    while (front <= tail)
    {
        int u = q[front++];
        for (int i = head[u]; ~i; i = net[i])
        {
            int v = ver[i];
            if (d[v] == -1 && cpt[i])
            {
                d[v] = d[u] + 1;
                cur[v] = head[v];
                if (v == T)
                    return true;
                q[++tail] = v;
            }
        }
    }
    return false;
}

int find(int u, int limit)
{
    if (u == T)
        return limit;
    int flow = 0;
    for (int i = cur[u]; ~i && flow < limit; i = net[i])
    {
        cur[u] = i;
        int v = ver[i];
        if (d[v] == d[u] + 1 && cpt[i])
        {
            int x = find(v, min(limit - flow, cpt[i]));
            if (!x)
                d[v] = -1;
            cpt[i] -= x, cpt[i ^ 1] += x, flow += x;
        }
    }
    return flow;
}

int dinic()
{
    int res = 0, flow;
    while (bfs())
    {
        while (flow = find(S, INF))
            res += flow; 
    }
    return res;
}

int main()
{
    int m, n;
    scanf("%d%d", &m, &n);
    memset(head, -1, sizeof(head));
    S = 0, T = n + 1;
    for (int i = 1; i <= m; i++)
        add(S, i , 1), add(i, S ,0);
    for (int i = m + 1; i <= n; i++)
        add(i, T, 1), add(T, i, 0);
    int u, v;
    while (scanf("%d %d", &u, &v) && ~u && ~v)
    {
        add(u, v, 1), add(v, u, 0);        
    }
    printf("%d\n", dinic());
    for (int i = 0; i < idx; i += 2)
        if (!cpt[i] && ver[i] > m && ver[i] <= n)
            printf("%d %d\n", ver[i ^ 1], ver[i]);
    return 0;
}

二分图多重匹配

P3254 圆桌问题
这道题如果用匈牙利算法就做不出来了
建图方式与二分图匹配差不多,只不过边的容量有所改变而已

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N = 505, M = 2e5 + 5, INF = 1e8;

int n, m, S, T;
int head[N], ver[M], net[M], cpt[M], idx;
int q[N], cur[N], d[N], R[N], C[N], ans[N][N];

void add(int a, int b, int c)
{
    net[idx] = head[a], ver[idx] = b, cpt[idx] = c, head[a] = idx++;
    net[idx] = head[b], ver[idx] = a, cpt[idx] = 0, head[b] = idx++;
}

bool bfs()
{
    int front = 0, tail = 0;
    memset(d, -1, sizeof(d));
    q[0] = S, d[S] = 0, cur[S] = head[S];
    while (front <= tail)
    {
        int u = q[front++];
        for (int i = head[u]; ~i; i = net[i])
        {
            int v = ver[i];
            if (d[v] == -1 && cpt[i])
            {
                d[v] = d[u] + 1;
                cur[v] = head[v];
                if (v == T)
                    return true;
                q[++tail] = v;
            }
        }
    }
    return false;
}

int find(int u, int limit)
{
    if (u == T)
        return limit;
    int flow = 0;
    for (int i = cur[u]; ~i && flow < limit; i = net[i])
    {
        cur[u] = i;
        int v = ver[i];
        if (d[v] == d[u] + 1 && cpt[i])
        {
            int x = find(v, min(limit - flow, cpt[i]));
            if (!x)
                d[v] = -1;
            cpt[i] -= x, cpt[i ^ 1] += x, flow += x;
        }
    }
    return flow;
}

int dinic()
{
    int res = 0, flow;
    while (bfs())
    {
        while (flow = find(S, INF))
            res += flow;
    }
    return res;
}

int main()
{
    int flux = 0;
    scanf("%d%d", &m, &n);
    memset(head, -1, sizeof(head));
    S = 0, T = n + m + 1;
    for (int i = 1; i <= m; i++)
    {
        scanf("%d", &R[i]);
        add(S, i, R[i]), flux += R[i];
    }
    for (int i = m + 1; i <= m + n; i++)
    {
        scanf("%d", &C[i]);
        add(i, T, C[i]);
        for (int j = 1; j <= m; j++)
            add(j, i, 1);            
    }
    if (dinic() == flux)
        printf("1\n");
    else
    {
        printf("0");
        return 0;        
    }
    for (int i = 0; i < idx; i += 2)
    {
        if (cpt[i ^ 1] && ver[i] > m && ver[i] <= m + n)
            ans[ver[i ^ 1]][++ans[ver[i ^ 1]][0]] = ver[i] - m;
    }
    for (int i = 1; i <= m; i++)
    {
        for (int j = 1; j <= ans[i][0]; j++)
            printf("%d ", ans[i][j]);
        printf("\n");
    }
    return 0;
}   

无源汇上下界可行流

例题2188. 无源汇上下界可行流
这道题与流网络的是,这道题没有给出源点汇点,并且每条边有一个下界,那么我们考虑将它转化为一个流网络
假设原图中的流量为\(f(u,v)\),下界为\(c_l(u,v)\),上界为\(c_u(u,v)\)
那么\(c_l(u,v) \le f(u,v) \le c_u(u,v) \Rightarrow 0 \le f(u,v)-c_l(u,v) \le c_u(u,v)-c_l(u,v)\)
\(c'(u,v)=c_u(u,v)-c_l(u,v)\)即为转化后的容量限制
那么转化后是否满足流量守恒呢?
显然是不一定的
因为原图的流量是守恒的,并且对于每一个点,每一条入边与每一条出边所减去的\(c_l\)是不一样的,所以不能保证一定是相等的
那么该如何解决,我们设\(c_{in},c_{out}\)为该点所有的减去的容量
如何\(c_{in}>c_{out}\)那么从源点连一条容量为\(c_{in}-c_{out}\)的边,小于0则连向汇点
那么可以知道,若原图存在一个可行流,那么就说明新图从S流出的边一定是流满了的
那么判断原图存不存在可行流只需要判断新图存不存在流满的情况即可
代码

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N = 205, M = 20405, INF = 1e8;

int n, m, S, T;
int head[N], ver[M], net[M], cpt[M], idx;
int q[N], cur[N], d[N], cm[M], in[N], out[N];

void add(int a, int b, int up, int low)
{
    net[idx] = head[a], ver[idx] = b, cpt[idx] = up - low, cm[idx] = low, head[a] = idx++;
    net[idx] = head[b], ver[idx] = a, cpt[idx] = 0, cm[idx] = low, head[b] = idx++;
}

bool bfs()
{
    int front = 0, tail = 0;
    memset(d, -1, sizeof(d));
    q[0] = S, d[S] = 0, cur[S] = head[S];
    while (front <= tail)
    {
        int u = q[front++];
        for (int i = head[u]; ~i; i = net[i])
        {
            int v = ver[i];
            if (d[v] == - 1 && cpt[i])
            {
                d[v] = d[u] + 1;
                cur[v] = head[v];
                if (v == T)
                    return true;
                q[++tail] = v;
            }
        }
    }
    return false;
}

int find(int u, int limit)
{
    if (u == T)
        return limit;
    int flow = 0;
    for (int i = cur[u]; ~i && flow < limit; i = net[i])
    {
        cur[u] = i;
        int v = ver[i];
        if (d[v] == d[u] + 1 && cpt[i])
        {
            int x = find(v, min(limit - flow, cpt[i]));
            if (!x)
                d[v] = -1;
            cpt[i] -= x, cpt[i ^ 1] += x, flow += x;
        }
    }
    return flow;
}

int dinic()
{
    int res = 0, flow;
    while (bfs())
    {
        while (flow = find(S, INF))
            res += flow;
    }
    return res;
}

int main()
{
    int flux = 0;
    scanf("%d%d", &n, &m);
    memset(head, -1, sizeof(head));
    S = 0, T = n + 1;
    for (int i = 1; i <= m; i++)
    {
        int u, v, Max, Min;
        scanf("%d%d%d%d", &u, &v, &Min, &Max);
        add(u, v, Max, Min);
        in[v] += Min, out[u] += Min;
    }
    for (int i = 1; i <= n; i++)
    {
        // cout << in[i] - out[i] << endl;
        if (in[i] - out[i] > 0)
            add(S, i, in[i] - out[i], 0), flux += in[i] - out[i];
        else
            add(i, T, out[i] - in[i], 0);
    }
    if (flux == dinic())
    {
        printf("YES\n");
        for (int i = 0; i < (m << 1); i += 2)
            printf("%d\n", cpt[i ^ 1] + cm[i]);
    }
    else
        printf("NO");
    return 0;
}

妈的太多了写不完了