平衡树模板

例题P3369 【模板】普通平衡树

概念： 平衡树是二叉搜索树和堆合并构成的数据结构，它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

性质：对于每一个节点，满足它大于左儿子里的每一个节点，小于右儿子的每一个节点,即树的中序遍历为有序序列

对于一个平衡树，它可以支持的操作有
1:插入一个值
2:删除一个值
3:查询一个 \(x\) 的排名
4:查询排名为 \(x\) 的值
5:查询严格小于 \(x\) 的最大值
6:查询严格大于 \(x\) 的最小值

时间复杂度:不论哪一种操作，所花的时间都和树的高度成正比。因此，如果共有n个元素，

那么平均每次操作需要 \(O(logn)\) 的时间,所以我们要尽量让这棵树随机.

那么对于每一个节点,我们可以这样定义

struct tr
{   
    int l, r;
    int siz, cnt, val, key;
} tree[N];

\(l,r\) 为树的左右儿子的编号,\(siz\) 为这棵子树的节点个数,\(val\) 为一个随机值,\(key\) 是维护的值, \(cnt\) 为当前值的个数

通过\(val,key\),我们可以让这棵树足够随机,只需要这棵树满足大根堆的性质,\(val\) 大的在上面.

首先是pushup,这里pushup的作用主要是更新子树大小,对于需要用到子树大小的题，则在更新时需要pushup

void pushup(ll p)
{
    tree[p].siz = tree[tree[p].l].siz + tree[tree[p].r].siz + tree[p].cnt;
}

新建一个节点

int get_node(int key)
{
    tree[++tot].key = key;
    tree[tot].val = rand();
    tree[tot].siz = tree[tot].cnt = 1;
    return tot;
}

在新建节点的时候,因为 \(val\) 是随机的,所以可能不满足大根对的性质,所以就需要一个操做交换两个节点,也就是左旋和右旋

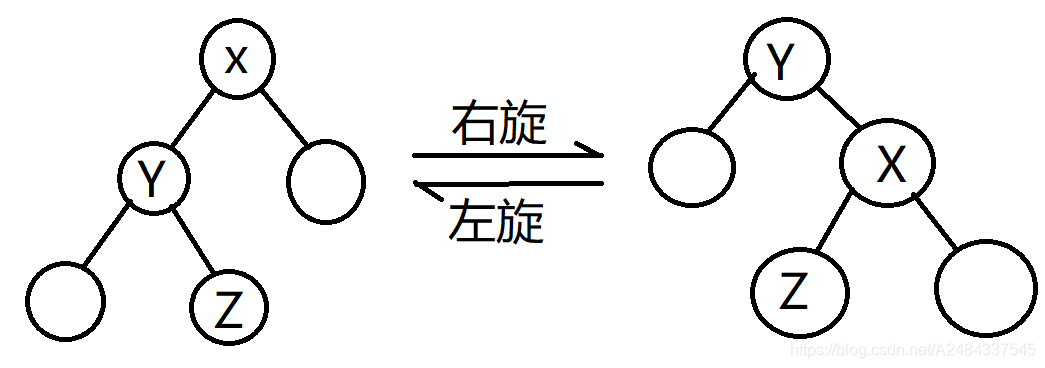
可以看出,在经过左旋或右旋后,树的中序遍历不变

通过图片可以写出代码

void zig(int &p)//这里需要加引用,因为左旋或右旋过后根节点会变
{
    int q = tree[p].l;
    tree[p].l = tree[q].r, tree[q].r = p, p = q;
    pushup(tree[p].r),pushup(q);
}

void zag(int &p)
{
    int q = tree[p].r;
    tree[p].r = tree[q].l, tree[q].l = p, p = q;
    pushup(tree[p].l),pushup(q);
}

对于插入操作,如果当前值存在,那么就先找到当前值然后cnt++,如果不存在就新建节点,具体看代码

void insert(int &p,int key)
{
    if(!p)
        p = get_node(key);//新建节点
    else if(tree[p].key==key)
        tree[p].cnt++;//个数加一
    else if(key<tree[p].key)
    {
        insert(tree[p].l, key);//如果加入的值在左子树
        if(tree[tree[p].l].val>tree[p].val)
            zig(p);//判断左子树的val是否会大于根节点
    }
    else 
    {
        insert(tree[p].r, key);//同上
        if(tree[tree[p].r].val>tree[p].val)
            zag(p);
    }
    pushup(p);
}

对于删除操作,其实和插入差不多,因为在中间删除节点很麻烦,所以就先将该接节点移到叶节点

void del(int &p,int key)
{
    if(!p)
        return;//如果不存在就直接返回
    if(tree[p].key==key)
    {
        if(tree[p].cnt>1)
            tree[p].cnt--;//如果节点个数大于一就减一
        else if(tree[p].l||tree[p].r)
        {
            if(!tree[p].r||tree[tree[p].l].val>tree[tree[p].r].val)//判断是否可以右旋
            {
                zig(p);
                del(tree[p].r, key);
            }
            else 
            {
                zag(p);
                del(tree[p].l, key);
            }
        }
        else//如果是叶节点就直接删除
            p = 0;
    }
    else if(key<tree[p].key)
        del(tree[p].l, key);//往左子树找
    else
        del(tree[p].r, key);//往右子树找
    pushup(p);
}

通过数值查询排名,具体看代码

int getrank(int p,int key)
{
    if(!p)
        return 1;
    if(tree[p].key==key)//如果找到了key,就等于左子树节点个数加一
        return tree[tree[p].l].siz + 1;
    else if(key<tree[p].key)//小于该节点就说明在左子树
        return getrank(tree[p].l, key);//大于就说明排名为左子树大小加该节点数量加右子树内的排名
    return getrank(tree[p].r, key) + tree[tree[p].l].siz + tree[p].cnt;
}

通过排名查询数值

int getkey(int p,int rank)
{
    if(!p)
        return INF;
    if(tree[tree[p].l].siz>=rank)
        return getkey(tree[p].l, rank);//如果左子树大小大于排名,就说明在左子树内
    else if(tree[tree[p].l].siz+tree[p].cnt>=rank)
        return tree[p].key;//如果加上根节点的数量大于排名,就说明树根节点的值
    return getkey(tree[p].r, rank - tree[tree[p].l].siz - tree[p].cnt);//不然就在右子树
}

查找小于x的最大值和大于x的最小值

int getpre(int p,int key)
{
    if(!p)
        return -INF;//没找到
    if(tree[p].key>=key)
        return getpre(tree[p].l, key);//找左子树内的最大值
    return max(tree[p].key, getpre(tree[p].r, key));//因为跟节点也满足条件,所以取个max
}

int getnet(int p,int key)
{
    if(!p)
        return INF;
    if(tree[p].key<=key)//原理同上
        return getnet(tree[p].r, key);
    return min(tree[p].key, getnet(tree[p].l, key));
}