洛谷 P10145 [WC/CTS2024] 线段树 题解--zhengjun

提供一种考场做法，在思路上和官方题解的差异蛮大的，虽然结果差不多。

首先需要发现 $[l,r)$ 区间可以算出来的充要条件是：

如果对于每个选中的节点 $u$，连无向边 $(L_u,R_u)$，则当且仅当 $l$ 和 $r$ 连通时区间 $[l,r)$ 可以算出来。

证明的话，用前缀和理解这些东西，分别考虑一下充分性和必要性即可，此处不赘述。

接下来，就考虑把这张图先连出来，大概长这样：

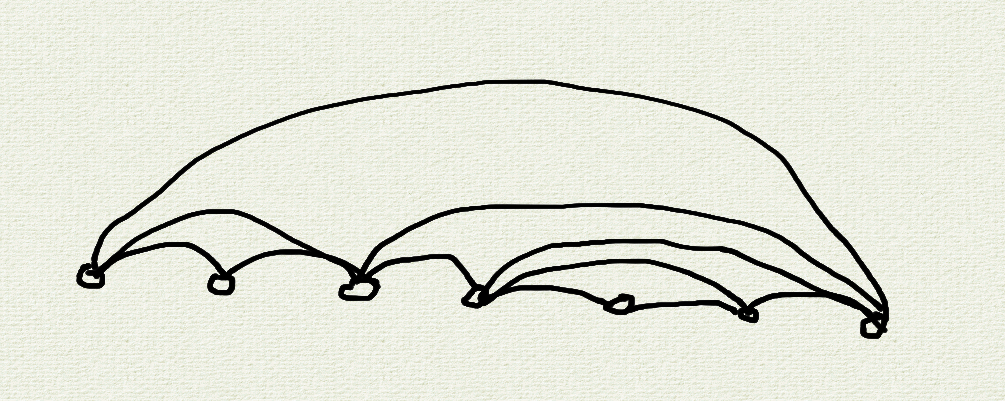
然后一组边的子集 $S$ 合法就是对于任意的 $L_i,R_i$，$L_i$ 和 $R_i$ 能够仅通过 $S$ 中的边连通。

接下来就是精髓了，同时本人做法和官方题解做法的分歧也就在这里。

发现这个东西一点都不优美，很难对 $m$ 个区间都考虑到，所以考虑转化一下。

具体地，对原图 $G$ 建立其对偶图 $G'$，大概长这样（蓝色部分）：

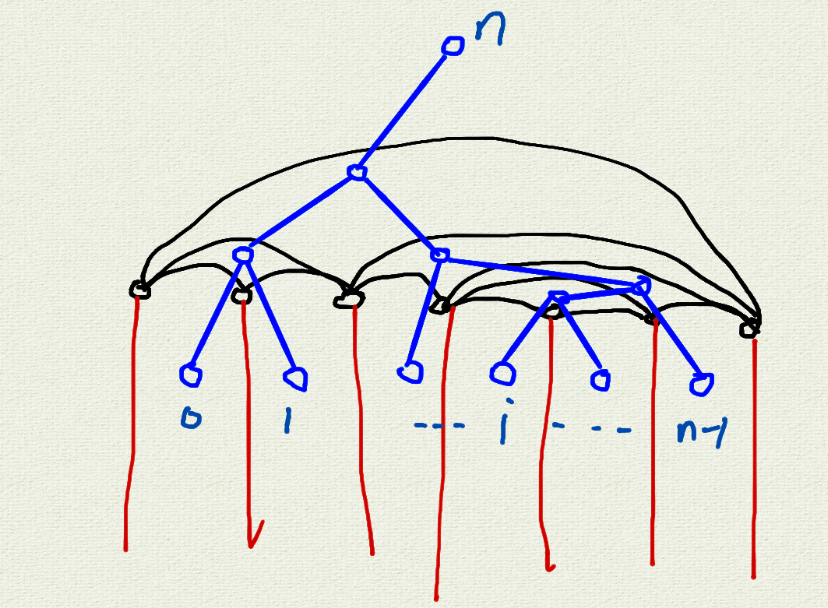
这样，在 $G$ 中 $L,R$ 连通等价于在 $G'$ 中，不存在 $[L,R)$ 区间内的叶子与 $[L,R)$ 区间外的叶子连通（使用了原图中路径和对偶图中的一组割对应的性质）。

虽然看起来更加不简洁，但是我们可以考虑什么样的两对点 $u,v$ 可以连通。

我们发现，当且仅当覆盖 $[u,u+1)$ 的区间集合与 $[v,v+1)$ 的区间集合相同时，$u,v$ 可以连通。

这样我们就可以考虑按照覆盖的集合进行染色为 $[1,k]$，$k$ 为颜色数，第 $i$ 个叶子的颜色为 $a_i$。

那么加上 $G'$ 是二叉树的良好性质，我们就可以设计 dp 了：

• $f_{u,c}$ 表示在 $u$ 的子树中，和 $u$ 连通的颜色为 $c$；
• $g_{u}$ 表示在 $u$ 的子树中，$u$ 不和任意一个叶子连通；

边界情况：对于 $[0,n)$ 的叶子结点 $u$，$f_{u,a_u}=1,g_{u}=0$。

转移是简单的，具体地：

$$\begin{aligned} g_u =&(2g_{ls_u}+\sum f_{ls_u,c})\times(2g_{rs_u}+\sum f_{rs_u,c})\\ f_{u,c}=&f_{ls_u,c}\times f_{rs_u,c}+\\ &f_{ls_u,c}\times (2g_{rs_u}+\sum f_{rs_u,c})+\\ &f_{rs_u,c}\times (2g_{ls_u}+\sum f_{ls_u,c}) \end{aligned}$$

总之就是讨论 $(u,ls_u),(u,rs_u)$ 是否存在。

然后使用线段树合并就能维护这个东西，时间复杂度 $\Theta(n\log n)$。

代码

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
using ull=unsigned long long;
#define all(a) (a).begin(),(a).end()
const int N=2e5+10,M=N*2,mod=998244353,K=N*20;
mt19937_64 rnd(time(0));
int n,m,k,ls[M],rs[M],id[M],a[N];
ull c[N];
vector<ull>num;
int build(int l=0,int r=n){
	int rt=++k,mid;
	if(l+1==r)return id[rt]=l,rt;
	id[rt]=-1;
	scanf("%d",&mid);
	ls[rt]=build(l,mid);
	rs[rt]=build(mid,r);
	return rt;
}
namespace SGT{
	struct node{
		int ls,rs,mul,sum;
		node(){ls=rs=sum=0,mul=1;}
	}t[K];
	int k;
	void pushup(int rt){
		t[rt].sum=(t[t[rt].ls].sum+t[t[rt].rs].sum)%mod;
	}
	void pushmul(int rt,int x){
		if(!rt)return;
		t[rt].sum=1ll*t[rt].sum*x%mod,t[rt].mul=1ll*t[rt].mul*x%mod;
	}
	void pushdown(int rt){
		if(t[rt].mul^1){
			pushmul(t[rt].ls,t[rt].mul);
			pushmul(t[rt].rs,t[rt].mul);
			t[rt].mul=1;
		}
	}
	void insert(int &rt,int x,int l=1,int r=num.size()){
		if(!rt)rt=++k;
		if(l==r)return ++t[rt].sum,void();
		int mid=(l+r)>>1;
		pushdown(rt);
		if(x<=mid)insert(t[rt].ls,x,l,mid);
		else insert(t[rt].rs,x,mid+1,r);
		pushup(rt);
	}
	int query(int rt,int x,int l=1,int r=num.size()){
		if(!rt)return 0;
		if(l==r)return t[rt].sum;
		int mid=(l+r)>>1;
		pushdown(rt);
		if(x<=mid)return query(t[rt].ls,x,l,mid);
		else return query(t[rt].rs,x,mid+1,r);
		pushup(rt);
	}
	void merge(int &x,int y,int gl,int gr,int l=1,int r=num.size()){
		if(!x)return x=y,pushmul(x,gl);
		if(!y)return pushmul(x,gr);
		if(l==r){
			t[x].sum=(1ll*t[x].sum*t[y].sum+1ll*t[x].sum*gr+1ll*gl*t[y].sum)%mod;
			return;
		}
		int mid=(l+r)>>1;
		pushdown(x),pushdown(y);
		merge(t[x].ls,t[y].ls,gl,gr,l,mid);
		merge(t[x].rs,t[y].rs,gl,gr,mid+1,r);
		pushup(x);
	}
}
int g[M],root[M];
void dfs(int u){
	if(~id[u]){
		SGT::insert(root[u],a[id[u]]);
	}else{
		dfs(ls[u]),dfs(rs[u]);
		g[u]=1ll*g[ls[u]]*g[rs[u]]%mod;
		SGT::merge(root[u]=root[ls[u]],root[rs[u]],g[ls[u]],g[rs[u]]);
	}
	g[u]=(g[u]*2ll+SGT::t[root[u]].sum)%mod;
}
int main(){
	freopen(".in","r",stdin);
	// freopen(".out","w",stdout);
	scanf("%d%d",&n,&m);
	build();
	for(int l,r;m--;){
		scanf("%d%d",&l,&r);
		ull val=rnd();
		c[l]^=val,c[r]^=val;
	}
	for(int i=0;i<=n;i++)c[i]^=c[i-1];
	num=vector<ull>{c,c+1+n};
	sort(all(num)),num.erase(unique(all(num)),num.end());
	for(int i=0;i<=n;i++)a[i]=lower_bound(all(num),c[i])-num.begin()+1;
	dfs(1);
	cout<<(g[1]+SGT::query(root[1],a[n]))%mod<<endl;
	return 0;
}