从集合的角度思考DP问题
从集合的角度思考DP问题
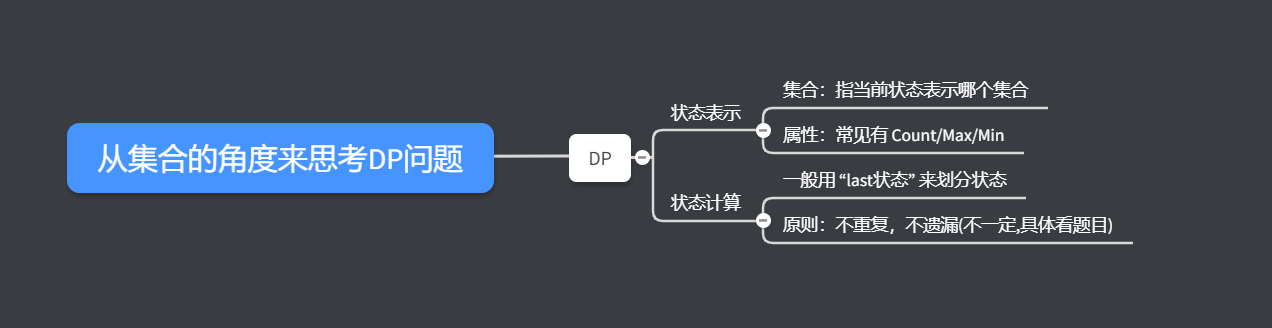
如上图展示了DP问题思考的一个简单步骤来自y总直播,“就像计算乘法一样,学会分析DP问题就像学会列竖式一样,让处理DP问题更简单”这就话让我瞬间意识到分析问题的重要性,处理DP问题不应该是想出转移过程,应该是一步步分析出来的。这篇博客记录以后做题过程中我对DP分析方法的理解和总结
#one. 杨老师的照相排列 (第一篇废话较多)
DP问题
- 这道题目前我解释不出为什么要用DP做,但Count是DP一类题型
分析过程
- DP一般就是一个状态向另一个状态转移,在这个过程中维护Count。分析的突破口就是last,在本题中就是给一个学生安排好位置。
- 这个学生安排好了位置,整个局面与把这个学生拿走的这个局面就构成了两个状态。当然我们现在还不能确定这就是可以解题的状态。
- 所以下一步我们就要试着去能不能从两个状态中找到更改Count的转移过程。
- 我们发现这个学生拿走后与拿走前Count是不变的,也就是两个局面满足条件的合影位置方案数相等。(其实之后正确理解应该是,原局面的Count在仅拿走一个学生时不改变)。这时候不要觉得dp[i]=dp[i-1]
- 就像博弈论一样,我们要找出拿走一名学生前的局面下面所有的子局面,就是可以转移到原局面的所有局面。由于是只移动一个学生,那么这个学生最多可以来自5行,所以找到有5种子局面。
- 接下来看能不能写出转移方程,写不出来前面分析屁用没有。
- 5个子局面都有达到这个子局面的方法数,加上一个学生不会增加原来的方法数,但是都变成了我们正在分析的局面,所以若用 \(Count()\)表示方法数,\(F,S_{1},S_{2},S_{3},S_{4},S_{5}\) 表示未拿走学生的局面和5种子局面,可得 \(Count(F)=\sum _{i=1} ^{i=5}Count(S_{i})\).
- 到现在,状态转移方程方程写出来了,接下来就是如何写代码了,这部分与博客主要内容无关就不写了。还有这里所有的局面其实就是状态,只是感觉状态像一个“点”,用局面能更好体现本题状态特点。
- 最后总结一下过程:先用last划分了状态,然后分析所有子状态,写出转移方程。
#two. 最长公共上升子序列
DP问题
- Max也是DP一类题型,而且问题规模可以缩小且,维护方式相同
分析过程
- 一定要重视 “last 操作”,现在感觉这是划分状态的关键,以及寻找当前状态上一个转移过来的状态时也应该从 “last-1 次操作”这个角度去考虑。
- 无论是二维数组,还是上一题五维数组,使用的原因是因为当前状态需要2/5个维数去定义,至于转移过程则还要考虑处理操作。
#three. 分形
DP问题
- Min也是DP一类题型,而且发现一般线型DP求最值会给序列,且N大小不大,还要要求一些递增递减条件
分析过程
- 这道题发现,如果DP问题以i为某个状态结束,其值会根据条件有许多情况, 受序列前面的值得影响,给人有一种一旦这一位值确定了,后面还有可能会修改,没有后效性的错觉。
- 这时候可以考虑二维j表示a[1...i]序列以b[j]这个值结束,其中b[]为第i位可取值集合。那么这个得到dp[i][j]就要遍历b[]的取值集合,按条件得到里面的最值,在算上末尾正在处理的这位来修改。
- 这一题和上一题都是这么处理的。
#four. 移动服务
DP问题
- 序列 + 最小化,这个题是计算路径转移时花费的问题,比较常见
分析过程
- 蓝书上面写了,求解线型DP先确定 “阶段”,如果“阶段”不足以表示这个状态,那就可以把所需的附加信息也作为状态的维度。这道题就是很容易想到以处理序列p[i]划分状态,但是这时候x,y,z的位置有好多。一定要明确的表示一个状态,“一一对应”。
- 同时当你想转移过程时,你发现当前状态的前一状态有很多,一开始我就一直在想如果遍历前面的状态,也打算想前面两题一样,维护个什么变量,但是发现“无后效性”。
- DP题的转移可以从前面依赖的状态转移过来,也可以从当前状态往后转移,这道题就是第二种,因为从之前转移它的数量不确定,可能很多。但是向后转移,每个状态只有三个转向的状态。
- 而且必须清楚,从一个阶段转移到另一个阶段,没必要关系附加信息维度的大小变化。因为无后效性由阶段保证
- 如果DP状态由多个维度表示,要检查各维度之间是否能相互导出,用最少的维度覆盖整个状态空间。
#five. 石子合并
DP问题
- 区间DP问题,一个特点就是一个区间状态由子区间得来。
分析过程
- 区间集合划分主要考虑l,r两个区间端点。然后就是k这个量 : \(dp[l][r] <- dp[l][k] + dp[k + 1][r]\);
- 注意在处理[l,r]区间时要保证子区间都处理好了,也就是一维遍历处理区间长度len,先处理长度为1的区间,再处理更长的区间
#six.
DP问题
- 因为可以合并任意几个相邻的节点,所以可以想到区间DP的方法
分析过程
- 这种 “任意选择一个位置断开,复制形成2倍长度的链” 的方法,是解决DP中环形结构的常用手段之一。(图源:《算法进阶指南》)

树形DP
#seven. 没有上司的舞会
总结
- 树形DP一般以节点从下到上的顺序作为DP的阶段,(从小问题到大问题)
- 树形DP一般采用dfs的方式,进入时赋初值,回溯时从子节点向父节点进行状态转移
选课
总结:
- 以x为根节点的子树选择num个课程的最大值 \(dp[x][num] = max(dp[x][num], dp[x][num - k] + dp[y][k]);\)
- 上面的方程是一个分组背包模型,每个子树看成一组嘛。这类题目称为背包类树形DP;
- 通常以节点编号作为阶段,我们也像线型DP一样将背包的体积作为第二维,在状态转移时我们要处理的实际上是分组背包问题
选课
总结:
- 以x为根节点的子树选择num个课程的最大值 \(dp[x][num] = max(dp[x][num], dp[x][num - k] + dp[y][k]);\)
- 上面的方程是一个分组背包模型,每个子树看成一组嘛。这类题目称为背包类树形DP;
- 通常以节点编号作为阶段,我们也像线型DP一样将背包的体积作为第二维,在状态转移时我们要处理的实际上是分组背包问题


 浙公网安备 33010602011771号
浙公网安备 33010602011771号