LIS最长上升子序列

首先需要知道，子串和子序列的概念，我们以字符子串和字符子序列为例，更为形象，也能顺带着理解字符的子串和子序列：

（1）字符子串指的是字符串中连续的n个字符，如abcdefg中，ab，cde，fg等都属于它的字串。

（2）字符子序列指的是字符串中不一定连续但先后顺序一致的n个字符，即可以去掉字符串中的部分字符，但不可改变其前后顺序。如abcdefg中，acdg，bdf属于它的子序列，而bac，dbfg则不是，因为它们与字符串的字符顺序不一致。

O(n^2)的DP，O(nlogn)的二分+贪心法，以及O(nlogn)的树状数组优化的DP。

 O(n^2)暴力DP

#include<bits/stdc++.h>

using namespace std;

int n;
int a[1010],f[1010];
int main() {
    cin>>n;
    a[0]=-2000000000;
    for(int i=1; i<=n; i++) cin>>a[i];
    for(int i=1; i<=n; i++)
        for(int j=0; j<i; j++)
            if(a[j]<a[i]) f[i]=max(f[i],f[j]+1);
    int ans=0;
    for(int i=1; i<=n; i++) ans=max(ans,f[i]);
    cout<<ans<<endl;
    return 0;
}

O(nlongn)二分+贪心,lower_bound

#include<bits/stdc++.h>
#define N 100010
using namespace std;

int n;
int a[N],q[N];
int main() {
    cin>>n;
    for(int i=1; i<=n; i++) cin>>a[i];
    int len=0;
    q[1]=-2e9;
    for(int i=1; i<=n; i++) {
        int l=1,r=len+1;
        while(l<r) {
            int mid=l+r+1>>1;
            if(q[mid]<a[i]) l=mid;
            else r=mid-1;
        }
        len=max(len,r);
        q[r+1]=a[i];
    }
    cout<<len<<endl;
    return 0;
}

#include<bits/stdc++.h>
#define N 100010
using namespace std;

int n;
int a[N],q[N];
int main() {
    cin>>n;
    for(int i=1; i<=n; i++) cin>>a[i];
    int len=0;
    q[1]=-2e9;
    for(int i=1; i<=n; i++) {
        int k=lower_bound(q+1,q+len+2,a[i])-q-1;
        len=max(len,k);
        q[k+1]=a[i];
    }
    cout<<len<<endl;
    return 0;
}

 

求出具体的数字（倒序输出）

#include<bits/stdc++.h>

using namespace std;

int n;
int a[1010],f[1010],g[1010];
int main() {
    cin>>n;
    a[0]=-2000000000;
    for(int i=1; i<=n; i++) cin>>a[i];
    for(int i=1; i<=n; i++)
        for(int j=0; j<i; j++)
            if(a[j]<a[i])
                if(f[i]<f[j]+1) g[i]=j,f[i]=f[j]+1;
    int k=1;
    for(int i=1; i<=n; i++)
        if(f[i]>f[k]) k=i;
    cout<<f[k]<<endl;
    for(int i=1,len=f[k]; i<=len; i++) cout<<a[k]<<" ",k=g[k];
    return 0;
}

 

 

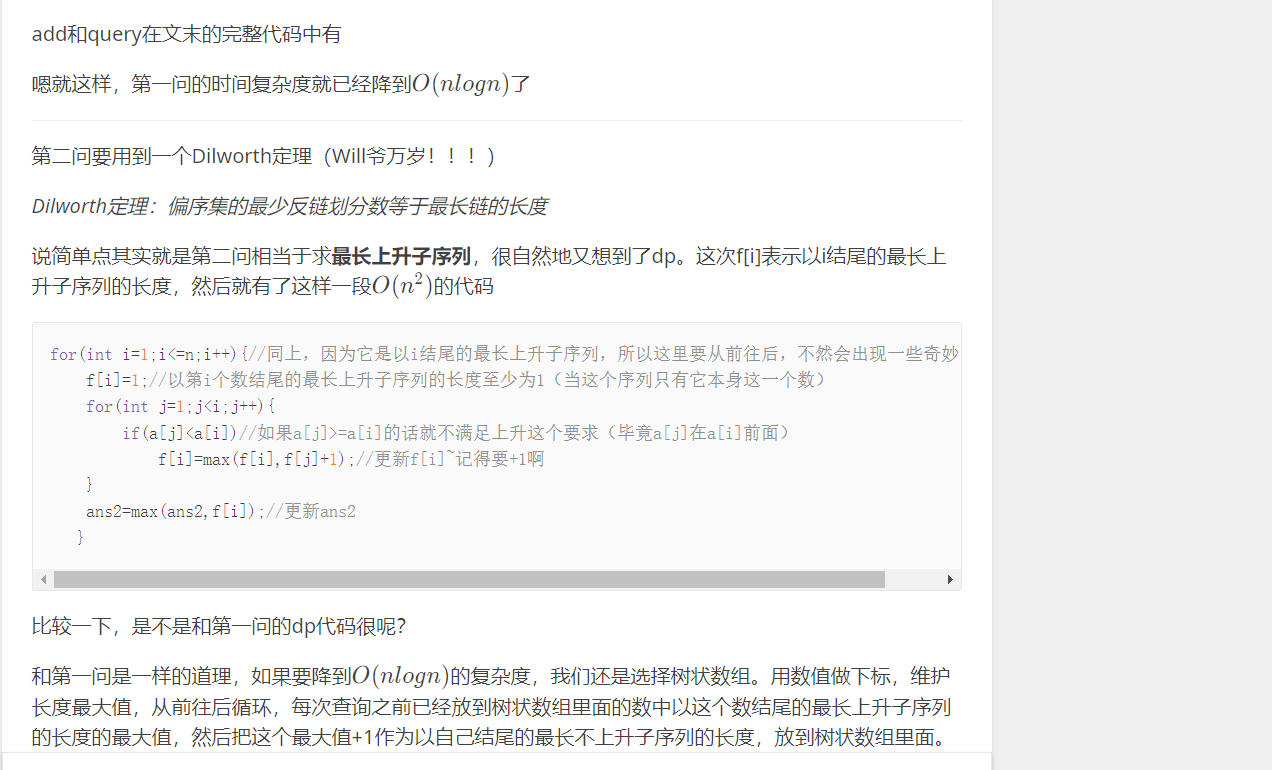
 Dilworth定理