前缀和与差分

前缀和

第一次写的时候，是想直接线性加起来。结果超时，因为是O(m*n)：

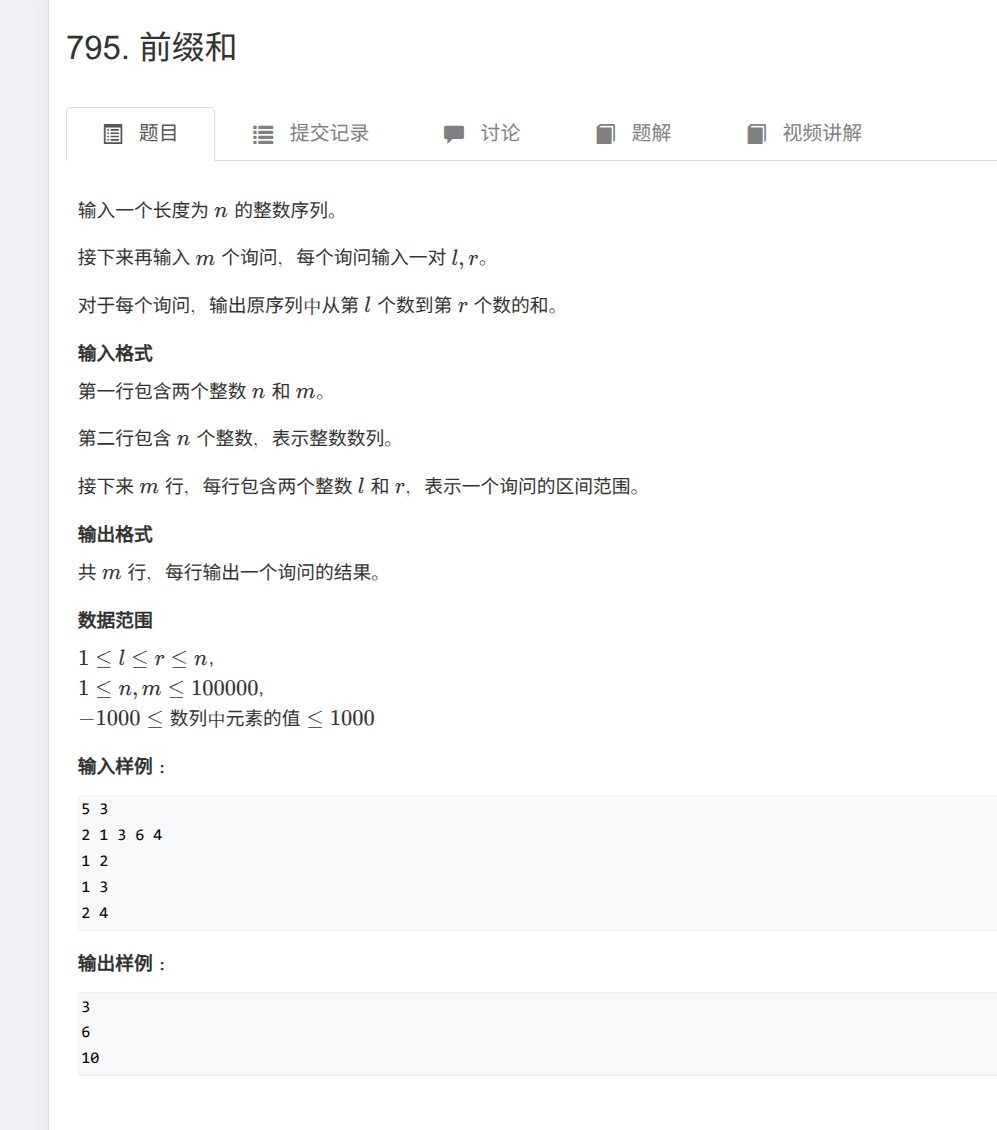
然后直接跟豆包学了一下，就是把全部先加起来，这个区间的和就是presum[rp-1]-presum[lp-2]

#include<stdio.h>

int n,m;
int P[100100]={0};
int presum[100100]={0};

void initpresum(int n){
    presum[0] = P[0];
    for(int i = 1; i < n; i++){
        presum[i] = presum[i-1]+P[i]; 
    }    
}
// 1 2 3 4 5 6
void query(int lp, int rp){
    printf("%d\n",presum[rp-1]-presum[lp-2]);
}

int main(){
    scanf("%d %d",&n,&m);
    int lp, rp;
    for(int i = 0; i < n; i++){
        scanf("%d",&P[i]);
    }
    initpresum(n);
    for(int i = 0; i < m; i++){
        scanf("%d %d",&lp,&rp);
        query(lp,rp);
    }
    
    return 0;
}

前缀和子矩阵

和上一题目一个原理就是变成矩阵就行，相当于前面两个矩阵相加减去多余部分，然后求两个点中间的时候也是类似的方法拼凑。像初中数学。

#include<stdio.h>
int P[1001][1001]={0};
int presum[1001][1001]={0};

void query(int x1, int y1, int x2, int y2){
    x1--;y1--;x2--;y2--;
    printf("%d\n",presum[x2][y2]-presum[x2][y1-1]-presum[x1-1][y2]+presum[x1-1][y1-1]);
    //printf("%d %d %d %d\n",presum[x2][y2],presum[x2][y1-1],presum[x1][y2-1],presum[x1][y1-1]);
}

void initpresum(int n, int m){
    presum[0][0] = P[0][0];
    presum[0][1] = presum[0][0]+P[0][1];
    presum[1][0] = presum[0][0]+P[1][0];
    
    for(int i = 0;i<n;i++){
        for(int j = 0; j<m;j++){
            if(i==0){
                presum[i][j] = presum[i][j-1]+P[i][j];
            }else if(j==0){
                presum[i][j] = presum[i-1][j]+P[i][j];
            }else{
                presum[i][j] = presum[i][j-1] + presum[i-1][j] - presum[i-1][j-1] + P[i][j];
            }
        }
    }
}

int main(){
    int n,m,q;
    int x1,y1,x2,y2;
    scanf("%d %d %d",&n,&m,&q);
    for(int i = 0;i<n;i++){
        for(int j = 0; j<m;j++){
            scanf("%d",&P[i][j]);
        }
    }
    initpresum(n,m);
    for(int i = 0;i<q;i++){
        scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
        query(x1,y1,x2,y2);
    }
    return 0;
}

差分

维护一个差分数组，数组的元素就是原来数组的前一个减去后一个。在处理l,r中间都加上c的情况，直接更新差分数组的l加上c然后r+1减去c,就行。恢复的时候就是用上一个加上差分数组元素，这样只需要一次就把全部都操作了，时间复杂度很低。

#include<stdio.h>
int P[100100]={0};
int diff[100100]={0};
int main(){
    int n,m;
    int l,r,c;
    scanf("%d %d",&n,&m);
    for(int i = 1; i<=n;i++)scanf("%d",&P[i]);
    //初始化diff数组
    diff[0]=0;
    for(int i = 1; i<=n;i++)diff[i]=P[i]-P[i-1];
    
    for(int i = 1; i<=m;i++){
        scanf("%d %d %d",&l,&r,&c);
        diff[l] += c;
        diff[r+1] -= c;
    }
    
    //恢复
    for(int i = 1; i<=n;i++){P[i]=P[i-1]+diff[i];printf("%d ",P[i]);}
    return 0;
}

差分矩阵

#include<stdio.h>
//矩阵可以稍微给大一点，1001的时候报错了。
int a[1002][1002]={0};
int diff[1002][1002]={0};

int main(){
    int n,m,q;
    int x1,x2,y1,y2,c;
    scanf("%d %d %d",&n,&m,&q);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            scanf("%d",&a[i][j]);
        }
    }
    //初始化差分矩阵
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            // a[i][j]相当于diff的前缀和，求他就是求对应的元素也就是把两边矩阵都剪掉得到对应元素
            diff[i][j] = a[i][j] - a[i-1][j] - a[i][j-1] + a[i-1][j-1];    
        }
    }
    
    for(int i=1;i<=q;i++){
        scanf("%d %d %d %d %d",&x1,&y1,&x2,&y2,&c);
        diff[x1][y1] +=c;
        diff[x2+1][y1] -=c;
        diff[x1][y2+1] -=c;
        diff[x2+1][y2+1] +=c;
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            //从上面diff的公式换过来
            a[i][j] = diff[i][j] + a[i-1][j] + a[i][j-1] - a[i-1][j-1];  
            printf("%d ",a[i][j]);
        }
        printf("\n");
    }    
    
    return 0;
}