Learning Discriminative Model Prediction for Tracking

Learning Discriminative Model Prediction for Tracking

论文 代码

Architecture

dimp主要强调了自己是一个具有端到端学习，并且可以在线更新的架构，因此并不像siamese系列只是计算一下模板和搜索区域的相关性，那样只利用了目标的外观信息，并没有利用背景信息。由此作者设计了一个discriminative learning的架构，经过几次的迭代就能预测一个有效的target model(因为tracking就是需要一种target-specific的信息)。这部分就类似ATOM里面的classification的部分，都是为了更好的区分target和distractor，如下图所示，而回归部分还是利用ATOM里面的IoU predictor.

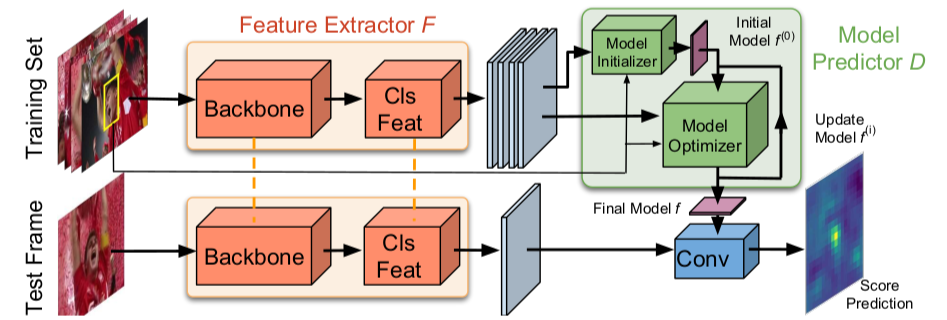
Model Predictor D

总体的流程就是用Model Initializer初始化一个\(Initial Model f^{(0)}\) ，然后送入Model Optimizer来\(Update Model f^{(i)}\) ，经过\(N_{iter}\)次迭代过后得到Final Model f，在这几次内部迭代过程中，以

\[\tag{1} L(f)=\cfrac{1}{S_{train}}\displaystyle\sum_{(x,c)\in S_{train}} ||r(x*f,c)||^2+||\lambda f||^2 \]

\[\tag{2} r(s,c)=v_c\ \cdot(m_cs+(1-m_c))max(0,s)-y_c \]

为损失函数来指导我们的优化过程，其中\(m_{c}\)是介于[0,1]之间的target_mask的一个map，\(v_{c}\)是起到空间不同位置赋予权重的spatial weight的一个map，\(y_{c}\)是目标的一个map，下面是他们的一个可视化图，最重要的一点就是他们都是可学习的【下面还要说，其实没什么，就是一层卷积层的输出；其实\(m_{c} s+\left(1-m_{c}\right)\max (0, s)\)用一个LeakyReLU函数就能实现】

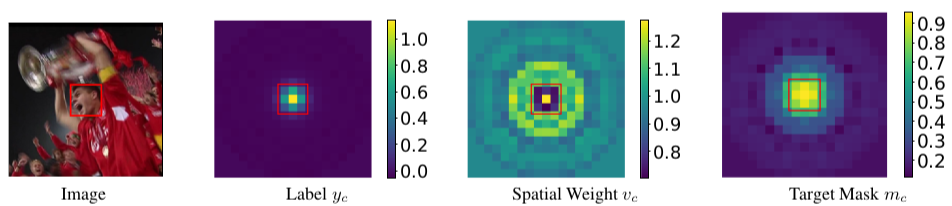
(2)中 \(v_c\) 是一个平衡正负样本数量的权重，类似于focal loss中的 \(\alpha\) ,为了看清 \(m_c\) 的作用，对以上损失做简单的推导，

\[r(s,c) = \begin{cases} v_c\ \cdot(s-y_c) &\text{, } s\gt 0 \\ v_c\ \cdot(m_cs-y_c) &\text{, } s\le 0 \end{cases} \]

可见，当打分大于0时，残差部分与原来的计算完全相同，而打分小于0时会对score值做一个压缩，使得易分的负样本所占损失的比例大大减小。这篇文章最厉害的不仅仅是提出来这样一个损失，并且对这个损失的优化策略进行了调整，而且在损失中的一些“超参数”如 \(m_c,v_c,\lambda\) 甚至标签设定值 \(y_c\) 也可以通过对数据的学习得到。

优化策略采用最速下降法，传统梯度下降法写作如下：

\[\tag{3} f^{(i+1)} = f^{(i)}-\alpha\nabla \text{L}\bigg(f^{(i)}\bigg) \]

损失函数可以用二次泰勒展开来拟合，但是这是高维函数，所以可以用下面的标准型来展开，其中 \(Q^{(i)}\) 是对称正定矩阵(Hessian矩阵)

\[\tag{4} \begin{aligned} \text{L}(f)&\approx\hat{\text{L}}(f) \\ &=\cfrac{1}{2}\bigg(f-f^{(i)}\bigg)^{\text{T}}\text{Q}^{(i)}\bigg(f-f^{(i)}\bigg)+\bigg(f-f^{(i)}\bigg)^{\text{T}}\nabla L\bigg(f^{(i)}\bigg)+L\bigg(f^{(i)}\bigg) \end{aligned} \]

在确定迭代方向为负梯度方向的前提上，需要确定在该方向上使得函数值最小的迭代步长\(\alpha\) ，这就是最速下降法和梯度下降法的区别所在，我们求导一下，可以得到：

\[\tag{5} \alpha= \cfrac{\nabla\text{L}\big(f^{(i)}\big)^{\text{T}}\nabla\text{L}\big(f^{(i)}\big)} {\nabla\text{L}\big(f^{(i)}\big)^{\text{T}}\text{Q}^{(i)}\nabla\text{L}\big(f^{(i)}\big)} \]

推导过程：最速下降法的核心是要迭代得到理想的步长，我们的目标是要走的每一步都可以使 \(L\big(f^{(i+1)}\big)\) 下降到不能再小，因此 \(L\big(f^{(i+1)}\big)\)对\(\alpha\) 求导:

\(\cfrac{d}{d\alpha}\hat L\big(f^{(i)}\big)=\cfrac{d}{d\alpha}\hat L\big(f^{(i)}-\alpha\nabla L(f^{(i)})\big)=0\)

推导过程如下

\[\begin{aligned} \text{L}(f)&\approx\hat{\text{L}}(f)& \\ &=\cfrac{1}{2}\big(f-f^{(i)}\big)^{\text{T}}\text{Q}^{(i)}\big(f-f^{(i)}\big)+\big(f-f^{(i)}\big)^{\text{T}}\nabla L\big(f^{(i)}\big)+L\big(f^{(i)}\big)\\ \cfrac{d}{d\alpha}\hat L\big(f^{(i)}\big) &=\cfrac{d}{d\alpha}\hat L\big(f^{(i)}-\alpha\nabla L(f^{(i)})\big)\\ &=\cfrac{d}{d\alpha}\bigg(\cfrac{1}{2}\big(-\alpha\nabla\text{L}(f^{(i)})\big)^{\text{T}}Q^{(i)}\big(-\alpha\nabla\text{L}(f^{(i)})\big)-\big(\alpha\nabla L(f^{(i)})\big)^{\text{T}}\nabla L\big(f^{(i)}\big)+L\big(f^{(i)}\big)\bigg)\\ &=\alpha\big(\nabla\text{L}(f^{(i)})\big)^{\text{T}}Q^{(i)}\big(\nabla\text{L}(f^{(i)})\big)-\big(\nabla L(f^{(i)})\big)^{\text{T}}\nabla L\big(f^{(i)}\big)\\ &=0\\ &\rArr (5) \end{aligned}\]

因为最普通的 \(Q^{(i)}\)就是二阶泰勒标准展开中的海森矩阵(Hessian matrix)，但涉及二次导，所以实际编程时用一阶导代替(Guass-Newton法):\(Q^{(i)}=\left(J^{(i)}\right)^{\mathrm{T}} J^{(i)}\)，因此在此处， Q^{(i)} 用 \(J^TJ\) 代替 \(Q^{(i)}=\left(J^{(i)}\right)^{\mathrm{T}} J^{(i)}\) 代入 \(\alpha\) 式中有:

\[\begin{aligned} \alpha &=\cfrac{\nabla\text{L}\big(f^{(i)}\big)^{\text{T}}\nabla\text{L}\big(f^{(i)}\big)} {\nabla\text{L}\big(f^{(i)}\big)^{\text{T}}\text{Q}^{(i)}\nabla\text{L}\big(f^{(i)}\big)}\\ &=\cfrac{\nabla\text{L}\big(f^{(i)}\big)^{\text{T}}\nabla\text{L}\big(f^{(i)}\big)} {\nabla\text{L}\big(f^{(i)}\big)^{\text{T}}\left(J^{(i)}\right)^{\mathrm{T}} J^{(i)}\nabla\text{L}\big(f^{(i)}\big)}\\ &=\cfrac{\nabla\text{L}\big(f^{(i)}\big)^{\text{T}}\nabla\text{L}\big(f^{(i)}\big)} {\left(J^{(i)}\nabla\text{L}(f^{(i)})\right)^{\mathrm{T}} \left(J^{(i)}\nabla\text{L}\big(f^{(i)}\big)\right)} \end{aligned}\]

令 \(h=J^{(i)}L(f^{(i)})\) ,则 \(\alpha\larr ||\nabla L\left(f^{(i)}\right)||^2/||h||^2\),更新策略为：

讲解链接