支持向量机

目录

• 支持向量机SVM (Support vector machine)
  • 超平面、间隔
  • 升维转换、核技巧（Kernel Trick）
    • 高斯核函数
  • 正负超平面间隔L
  • KKT条件证明
  • 原问题与对偶问题
  • 软间隔最优化问题

支持向量机SVM (Support vector machine)

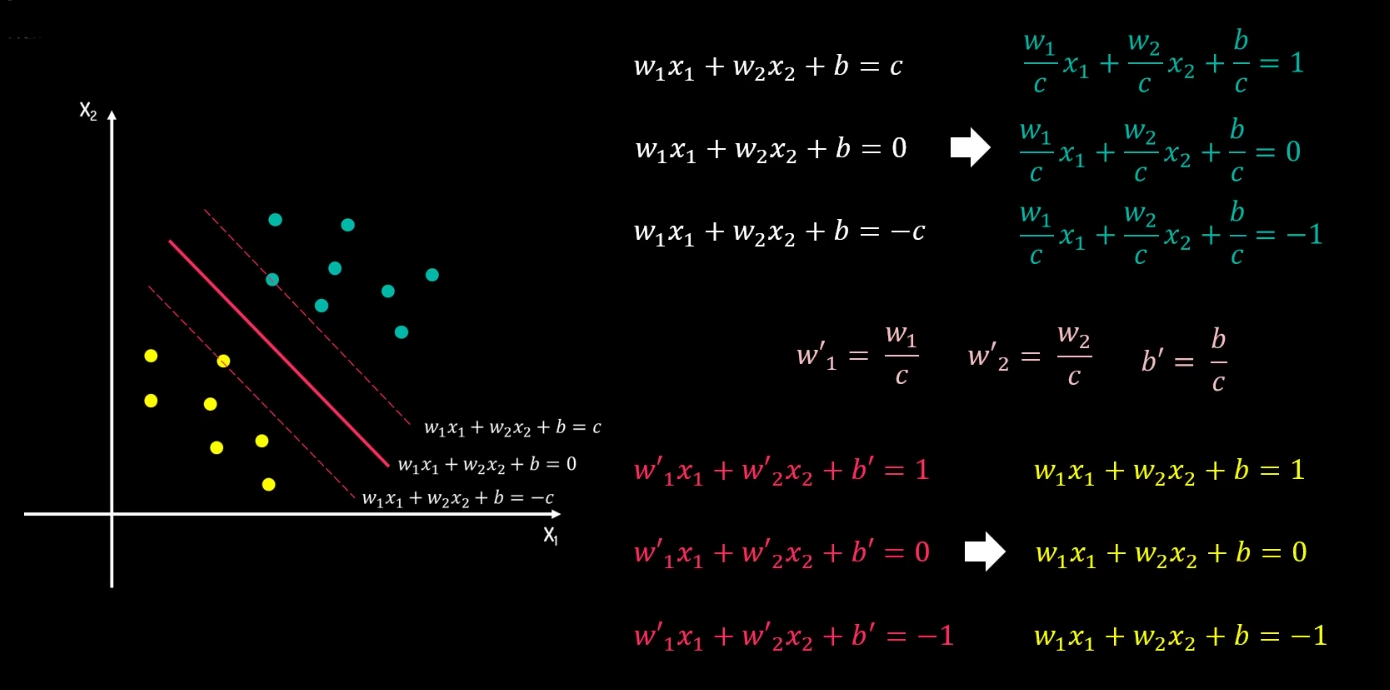
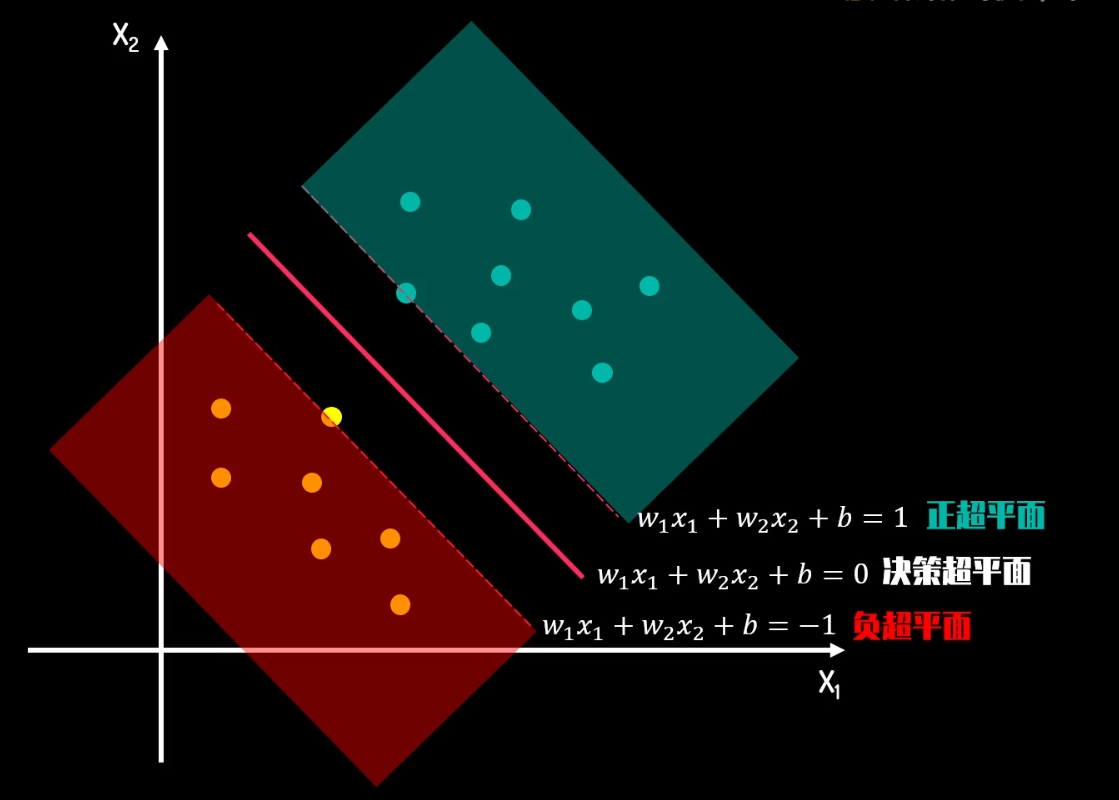
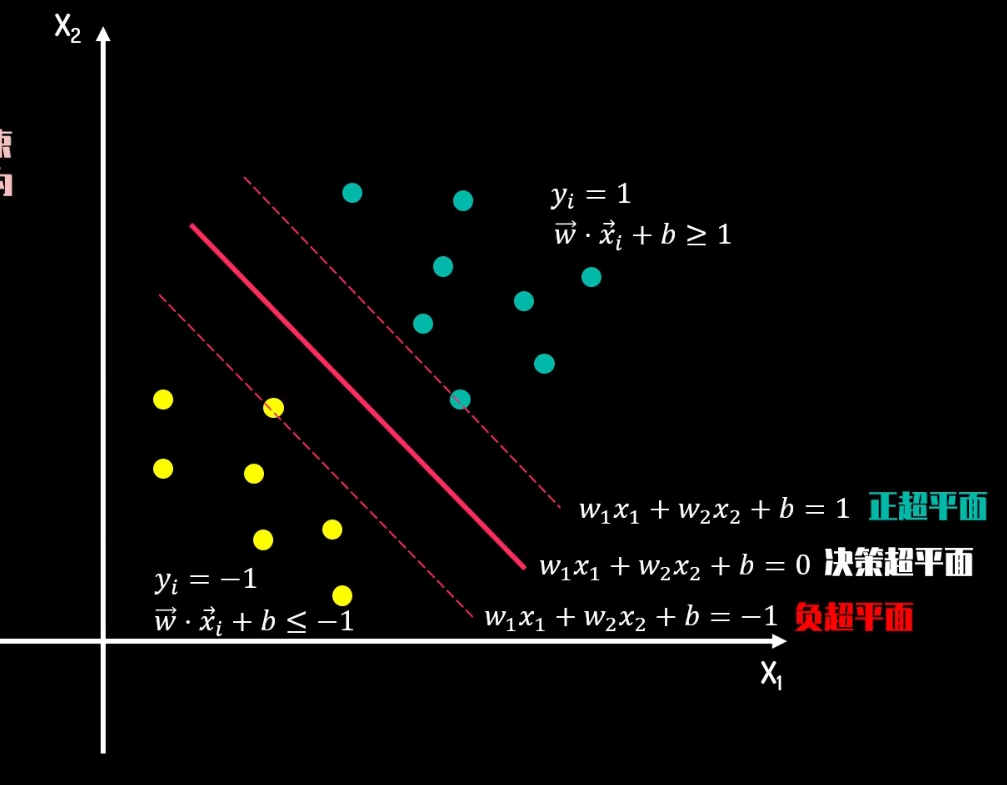
超平面、间隔

取超平面时间隔最大

升维转换、核技巧（Kernel Trick）

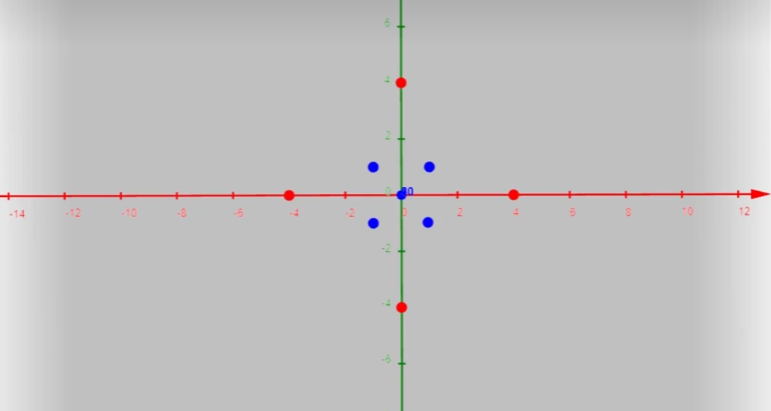
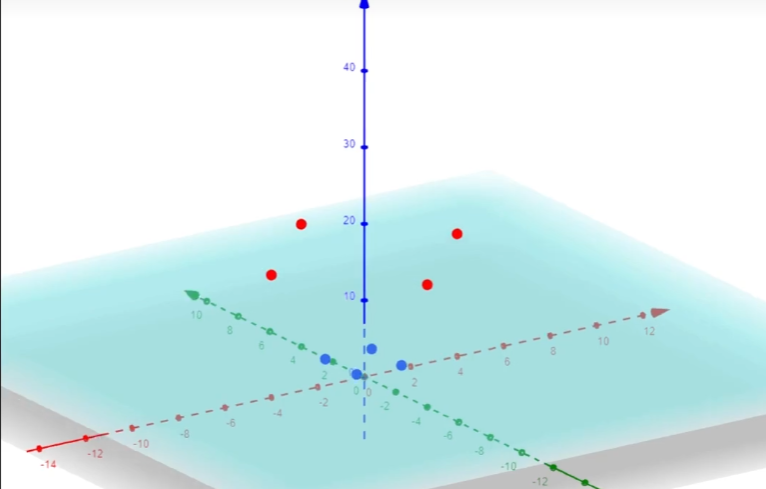
高斯核函数

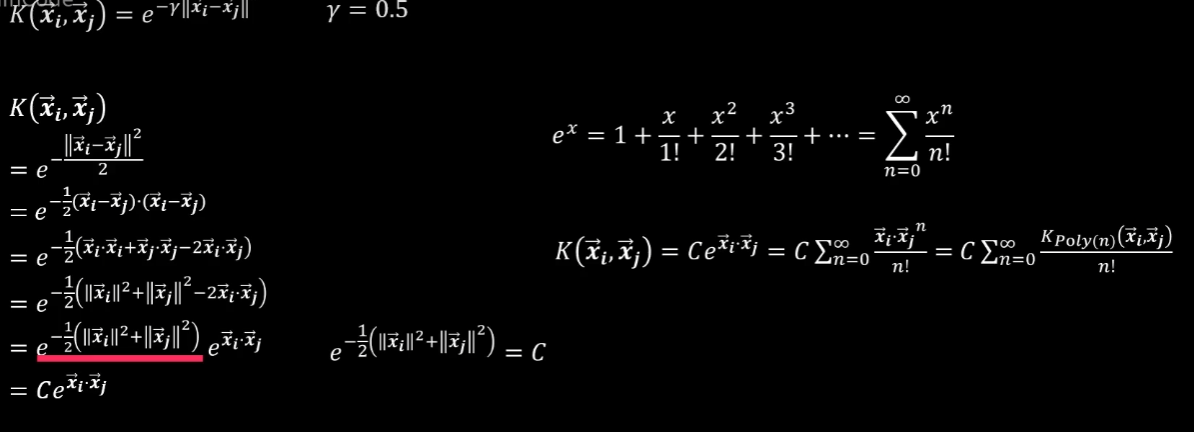
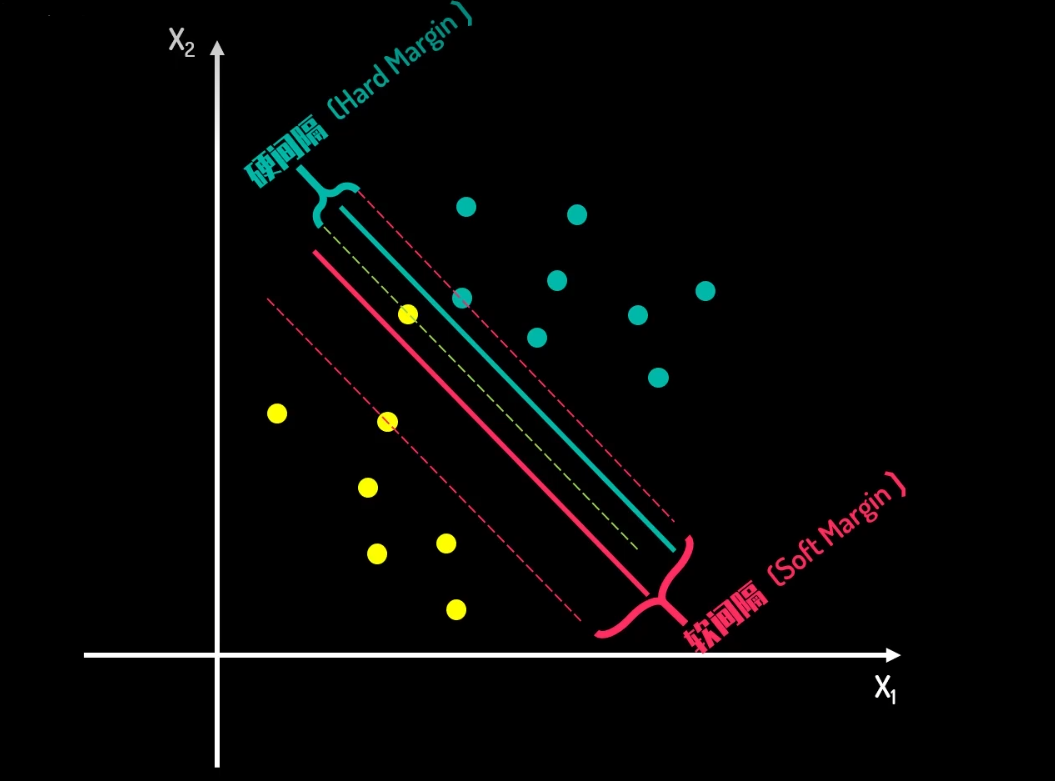
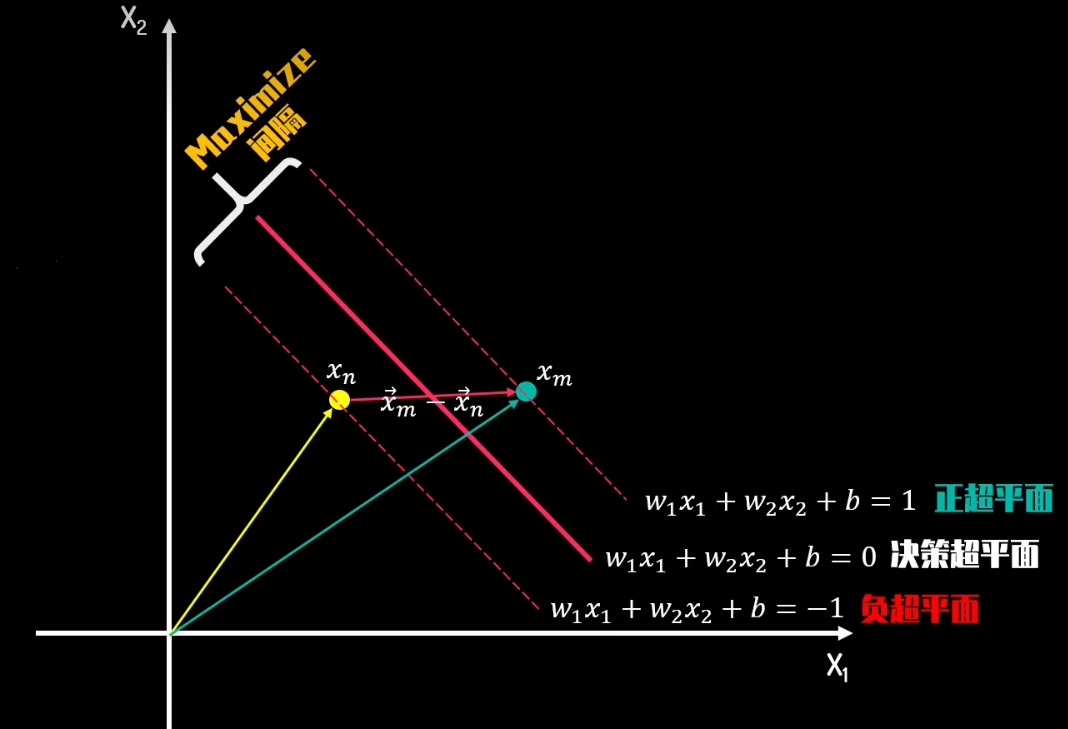
正负超平面间隔L

取点在正超平面 \(x_m\), 负超平面 \(x_n\), 决策超平面 \(x_p,x_o\)
向量点积 \(\overrightarrow{v}*\overrightarrow{w}=v_1*w_1+v_2*w_2+v_3*w_3=||v||*||w||*\cos{\theta}\)

1. \(w_1*x_{1m}+w_2*x_{2m}+b=1\)
2. \(w_1*x_{1n}+w_2*x_{2n}+b=-1\)
3. ①-②：\(w_1*(x_{1m}-x_{1n})+w_2*(x_{2m}-x_{2n})=2\)
4. \(\lrarr\)：\(\overrightarrow{w}*(\overrightarrow{x_m}-\overrightarrow{x_n})=2\)

5. \(w_1*x_{1p}+w_2*x_{2p}+b=0\)
6. \(w_1*x_{1o}+w_2*x_{2o}+b=0\)
7. ⑤-⑥：\(w_1*(x_{1p}-x_{1o})+w_2*(x_{2p}-x_{2o})=0\)
8. \(\lrarr\)：\(\overrightarrow{w}*(\overrightarrow{x_p}-\overrightarrow{x_o})=0\)

两向量点积结果为0，意味这在几何上两向量垂直

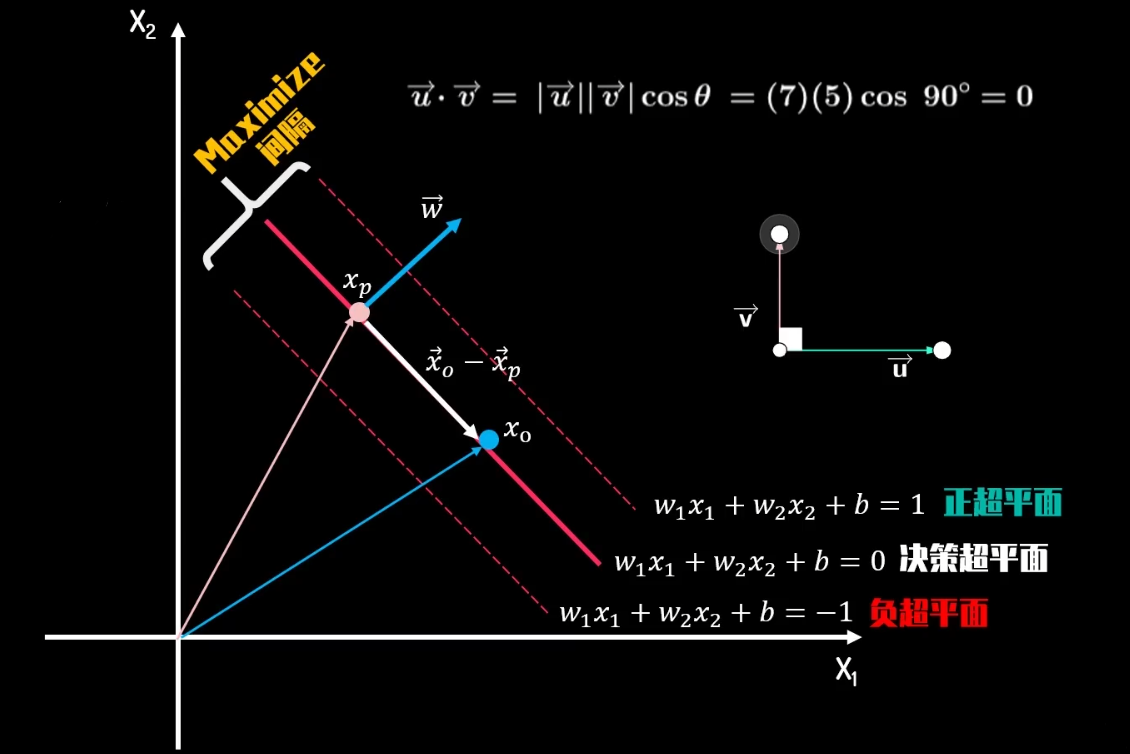
\(\because \overrightarrow{x_p}-\overrightarrow{x_o}在决策超平面上，且\overrightarrow{w}与\overrightarrow{x_p}-\overrightarrow{x_o}垂直\)

\(\therefore \overrightarrow{w}与决策超平面垂直\)

\(又\because \overrightarrow{w}*(\overrightarrow{x_m}-\overrightarrow{x_n})=2等价于||\overrightarrow{w}||*||\overrightarrow{x_m}-\overrightarrow{x_n}||*\cos \theta=2,\\ ||\overrightarrow{x_m}-\overrightarrow{x_n}||*\cos \theta为\overrightarrow{x_m}-\overrightarrow{x_n}在\overrightarrow{w}上的投影\)

\(\therefore ||\overrightarrow{x_m}-\overrightarrow{x_n}||*\cos \theta=L，即L=\cfrac{2}{||\overrightarrow{w}||}\)

\(\therefore 若使L最大，则\overrightarrow{w}长度最小\)

已知\(||\overrightarrow{w}||=\sqrt{w_1^2+w_2^2+\dots+w_n^2},\)求最小，可以简化为 \(f(w)=\cfrac{||\overrightarrow{w}||^2}{2}\) (去除根号，除2为了方便求导后约去2)

此时 \(g_i(w,b)=y_i*(\overrightarrow{w}*\overrightarrow{x_i}+b)-1\ge0,i=1,2,\dots,s,s为样本数\)

求f(w)最小，在条件\(g_i(w,b)\)为等式采用拉格朗日乘子法求最小，本条件为不等式。

对\(g_i(w,b)\)转换为等式：\(g_i(w,b)=y_i*(\overrightarrow{w}*\overrightarrow{x_i}+b)-1=p_i^2\ge 0,i=1,2,\dots,s,s为样本数\)

KKT条件证明

问题转换为：求\(f(w)=\cfrac{||\overrightarrow{w}||^2}{2}\)最小值，在\(g_i(w,b)=y_i*(\overrightarrow{w}*\overrightarrow{x_i}+b)-1=p_i^2,i=1,2,\dots,s\)条件下

由拉格朗日乘子法：设\(L(w,b,\lambda_i,p_i)=\cfrac{||\overrightarrow{w}||^2}{2}\ - \displaystyle\sum_{i=1}^{s}\lambda_i*\biggl[y_i*(\overrightarrow{w}*\overrightarrow{x_i}+b)-1-p_i^2\biggr]\)

1. \(\cfrac{\partial L}{\partial w}=\overrightarrow{w}-\displaystyle\sum_{i=1}^s\lambda_i*y_i*\overrightarrow{x_i}=0\) (L2范式)

2. \(\cfrac{\partial L}{\partial b}=-\displaystyle\sum_{i=1}^s\lambda_i*y_i=0\)

3. \(\cfrac{\partial L}{\partial \lambda_i}=-\bigg[y_i(\overrightarrow{w}*\overrightarrow{x_i}+b)-1-p_i^2\bigg]=0\)

4. \(\cfrac{\partial L}{\partial p_i}=2*\lambda_i*p_i=0\)

由4知：\(2*\lambda_i*p_i=0\rArr\lambda_i*p_i^2=0\)

由3等号两边同乘\(\lambda_i\)：\(\lambda_i\bigg[y_i(\overrightarrow{w}*\overrightarrow{x_i}+b)-1\bigg]=0\)

由题意知：\(g_i(w,b)\ge 0,\therefore g_i(w,b)=0或\lambda_i=0时，f(w)最小\)

\(\lambda_i\ge0\) (不懂)

KKT条件：

\(\overrightarrow{w}-\displaystyle\sum_{i=1}^s\lambda_i*y_i*\overrightarrow{x_i}=0\)

\(-\displaystyle\sum_{i=1}^s\lambda_i*y_i=0\)

\(y_i(\overrightarrow{w}*\overrightarrow{x_i}+b)-1\gt0\)

\(\lambda_i\bigg[y_i(\overrightarrow{w}*\overrightarrow{x_i}+b)-1\bigg]=0\)

\(\lambda_i\ge0\)

原问题与对偶问题

对偶问题例题

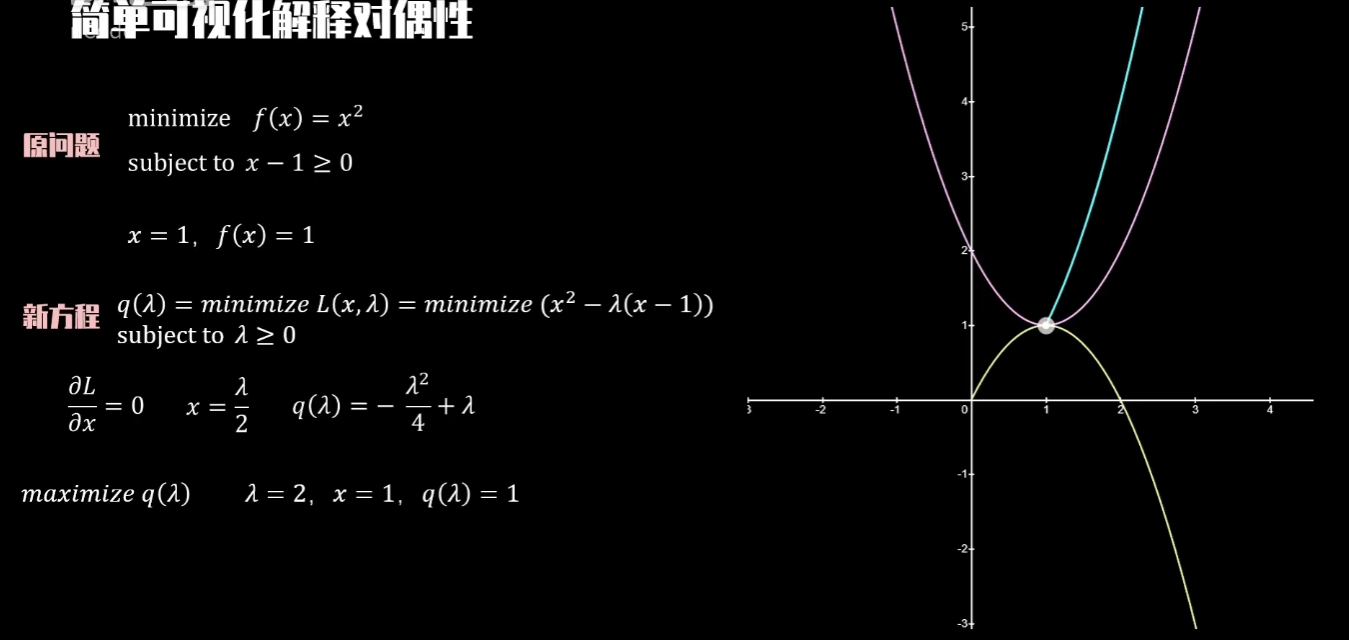
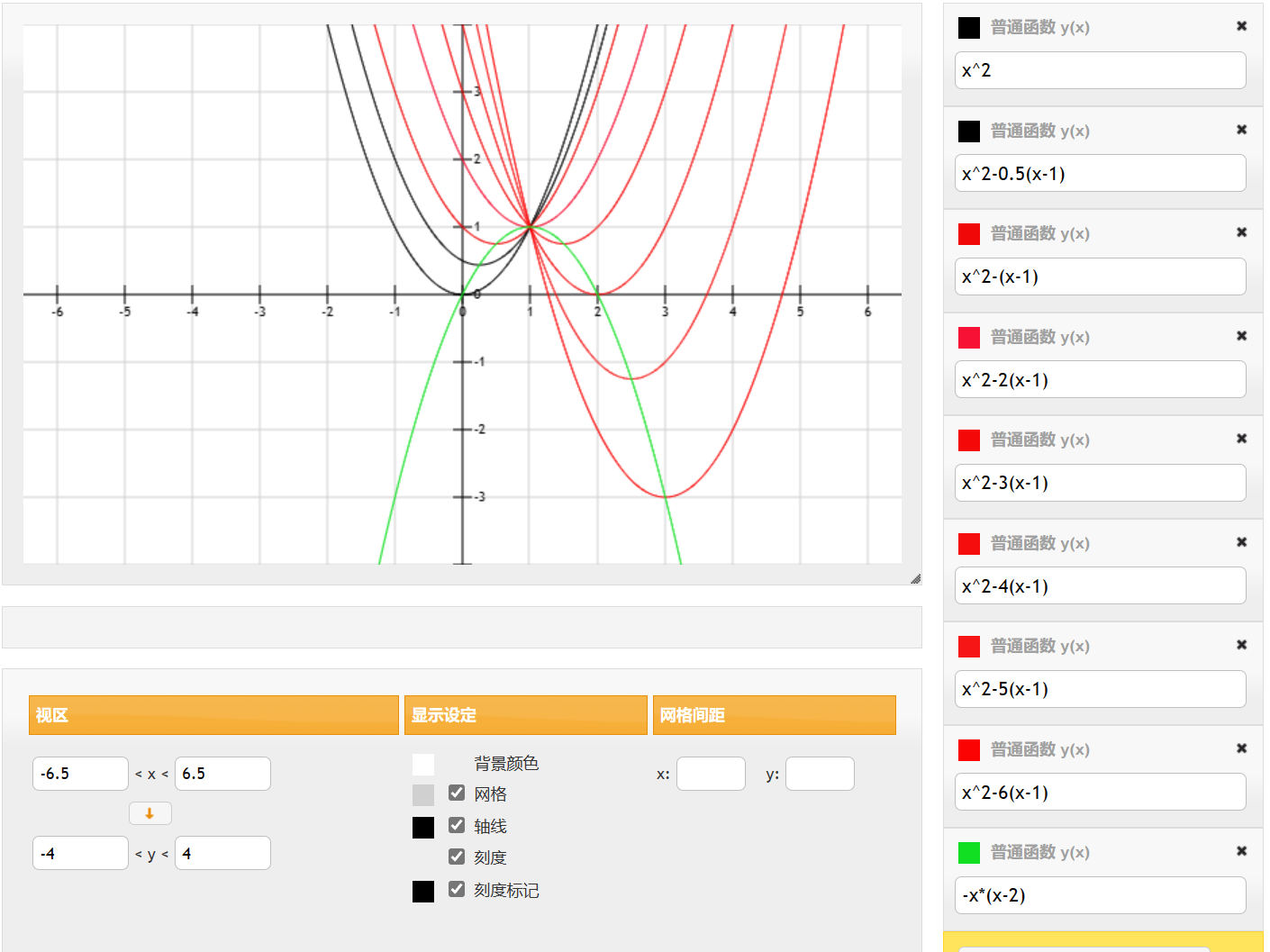
软间隔最优化问题