二叉树遍历

 

深度优先

前序遍历（根-左-右）：[a, b, d, g, h, c,e,i,f]

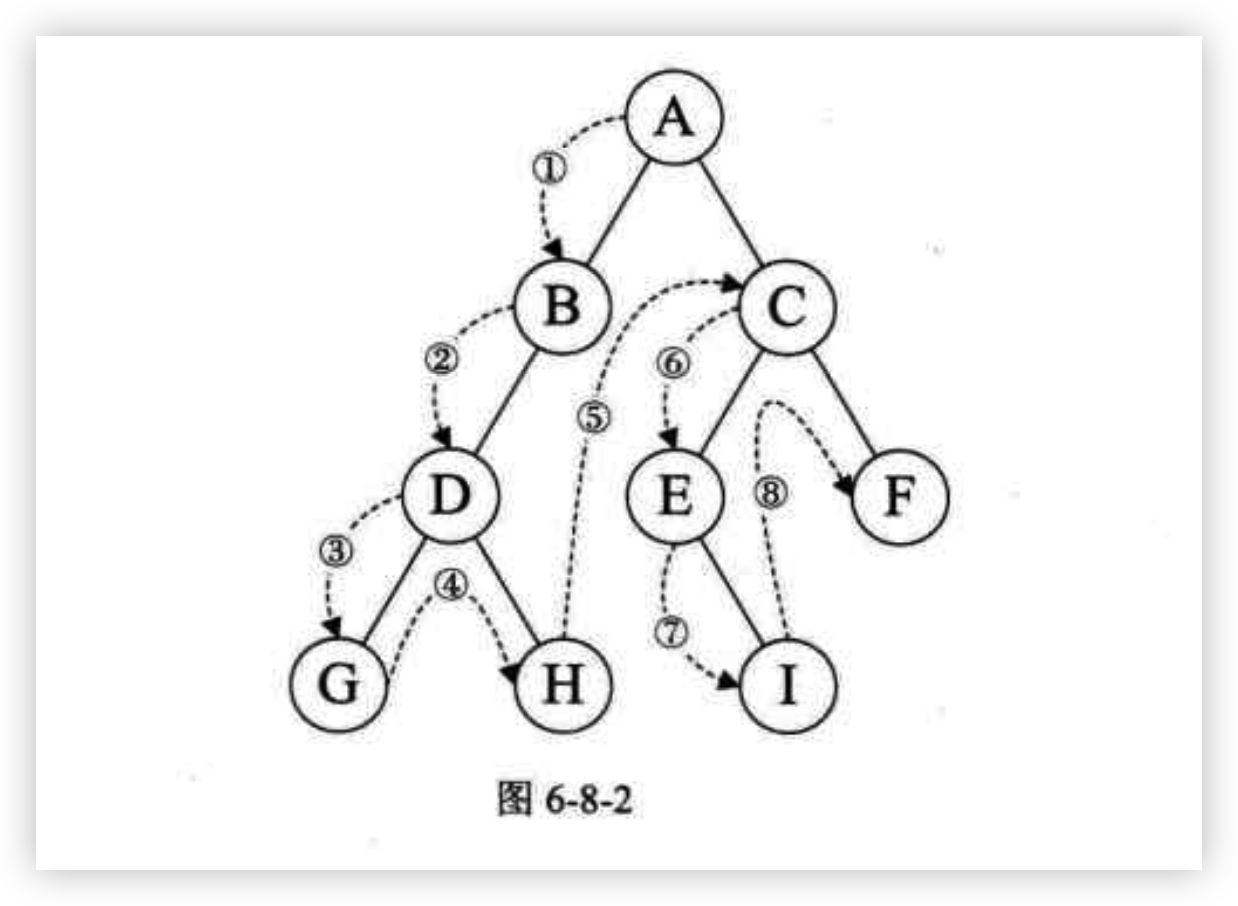
• 访问根节点
• 访问当前节点的左子树
• 若当前节点无左子树，则访问当前节点的右子树

递归版本:

function preorderTraversal(root) {
    if (root === null) return;
    // 访问根节点
    console.log(root.val);
    // 遍历左子树
    preorderTraversal(root.left);
    // 遍历右子树
    preorderTraversal(root.right);
}

优化版本：

function preOrder(root) {
    // 如果树为空，返回空数组
    if (!root) return [];
    // 用栈来模拟递归的过程
    const stack = [root];  // 初始时将根节点压入栈
    const result = [];     // 存储遍历结果
    // 遍历栈中的每个节点
    while (stack.length) {
        const node = stack.pop();  // 弹出栈顶节点
        result.push(node.val);     // 访问该节点，并将节点值保存到结果数组中

        // 由于栈是后进先出，要先访问左节点，所以先将右子节点入栈，再将左子节点入栈
        if (node.right) stack.push(node.right); 
        if (node.left) stack.push(node.left);
    }
    return result;  // 返回遍历结果
}

// 测试数据
const tree1 = {
    val: 1,
    left: {
        val: 2,
        left: { val: 4 },
        right: { val: 5 }
    },
    right: { val: 3 }
};

console.log('前序遍历 (根 -> 左 -> 右):', preOrder(tree1)); 
// 预期输出: [1, 2, 4, 5, 3]

 

中序遍历(左-根-右)：[g,d,h,b,a,e,i,c,f]


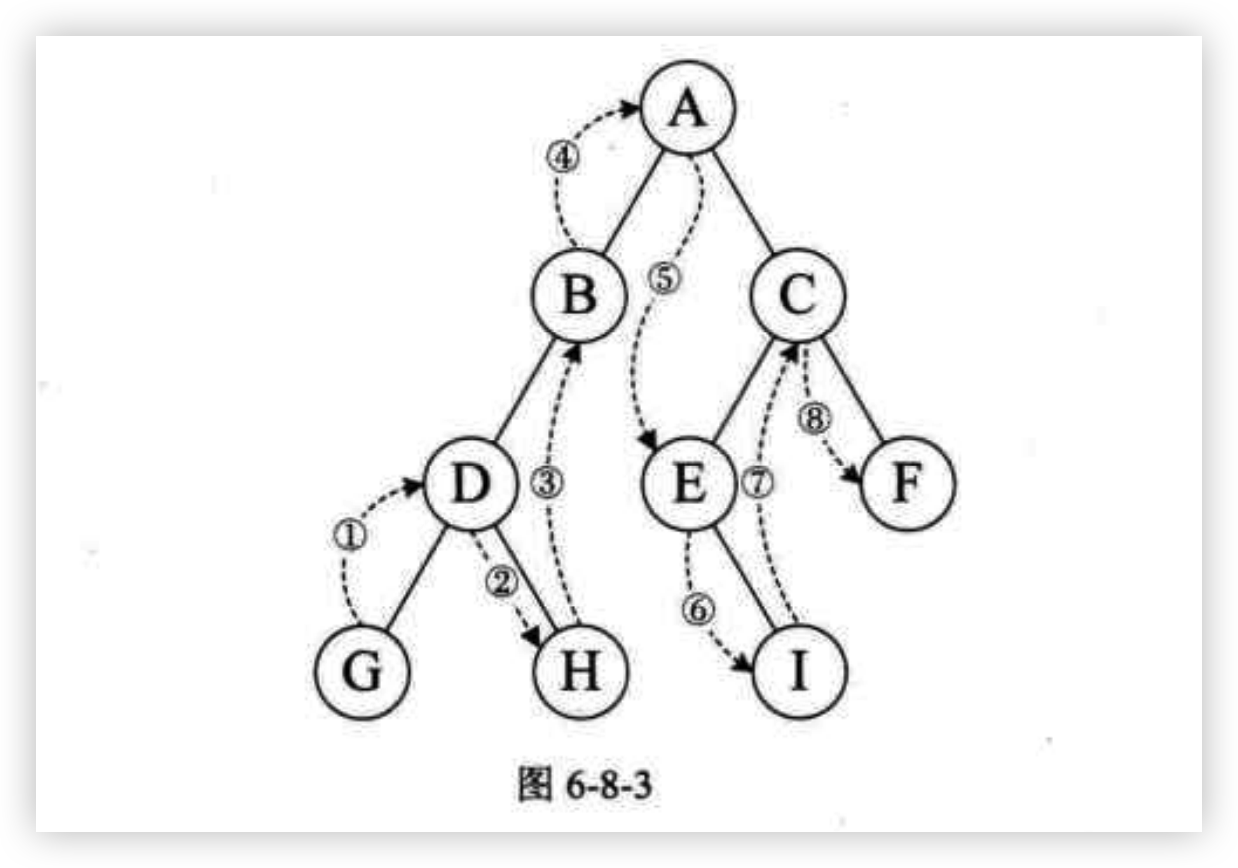
• 访问当前节点的左子树
• 访问根节点
• 访问当前节点的右子树

 递归版本：

function inorderTraversal(root) {
    if (root === null) return;
    // 遍历左子树
    inorderTraversal(root.left);
    // 访问根节点
    console.log(root.val);
    // 遍历右子树
    inorderTraversal(root.right);
}

 

优化版本:

function inOrder(root) {
    const result = [];  // 存储遍历结果
    const stack = [];   // 用栈来模拟递归的过程
    let current = root; // 从根节点开始
    // 当当前节点存在或者栈不为空时，继续遍历
    while (current || stack.length) {
        // 一直向左走，将所有左子节点压入栈
        while (current) {
            stack.push(current);  // 将当前节点压入栈
            current = current.left; // 移动到左子节点
        }
        // 弹出栈顶节点并访问
        current = stack.pop();  // 弹出栈顶节点
        result.push(current.val);  // 访问该节点并将其值保存到结果数组
        // 访问完左子树后，转向右子树
        current = current.right;
    }

    return result;  // 返回遍历结果
}

// 测试数据
console.log('中序遍历 (左 -> 根 -> 右):', inOrder(tree1)); 
// 预期输出: [4, 2, 5, 1, 3]

 

后序遍历：（左-右-根,若有子树，则先访问子树，子树也是左-右-根）:[g,h,d,b,i,e,f,c,a]

 

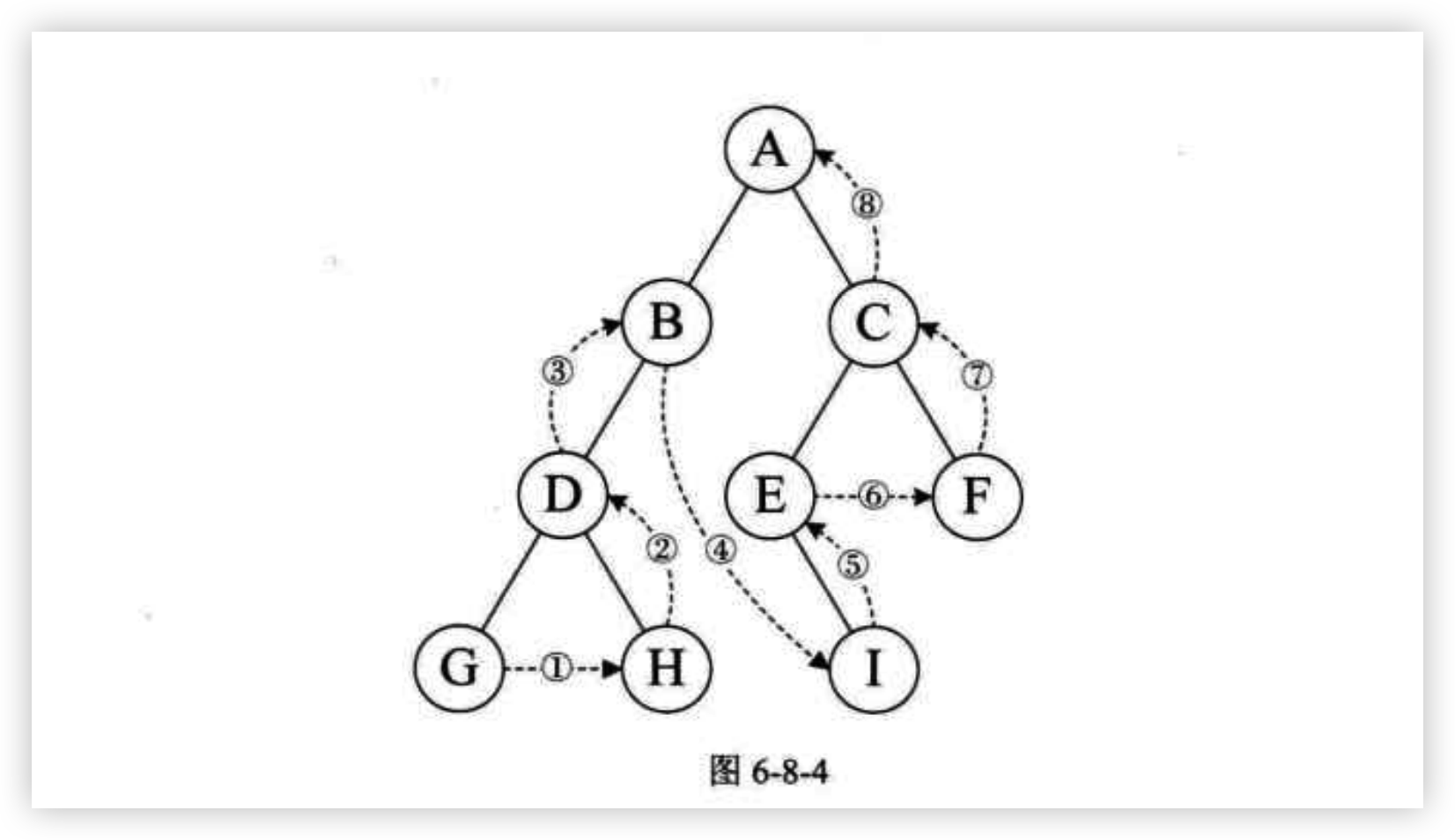
• 访问当前节点的左子树
• 访问当前节点的右子树
• 访问根节点

 递归版本：

function postorderTraversal(root) {
    if (root === null) return;
    // 遍历左子树
    postorderTraversal(root.left);
    // 遍历右子树
    postorderTraversal(root.right);
    // 访问根节点
    console.log(root.val);
}

 

优化版本:

function postOrder(root) {
    // 如果树为空，返回空数组
    if (!root) return [];

    const stack1 = [root];  // 用栈1来存储节点
    const stack2 = [];      // 用栈2来反转顺序
    const result = [];      // 存储遍历结果
    // 栈1模拟后序遍历顺序，根 -> 右 -> 左
    while (stack1.length) {
        const node = stack1.pop();  // 弹出栈1的栈顶节点
        stack2.push(node);          // 将弹出的节点压入栈2
        // 先将左子节点入栈，再将右子节点入栈
        if (node.left) stack1.push(node.left);  // 左子节点压栈
        if (node.right) stack1.push(node.right);  // 右子节点压栈
    }
    // 将栈2中的节点弹出并访问，得到左 -> 右 -> 根的顺序
    while (stack2.length) {
        const node = stack2.pop();  // 弹出栈2的栈顶节点
        result.push(node.val);      // 访问并保存节点值
    }
    return result;  // 返回遍历结果
}

// 测试数据
console.log('后序遍历 (左 -> 右 -> 根):', postOrder(tree1)); 
// 预期输出: [4, 5, 2, 3, 1]

 广度优先

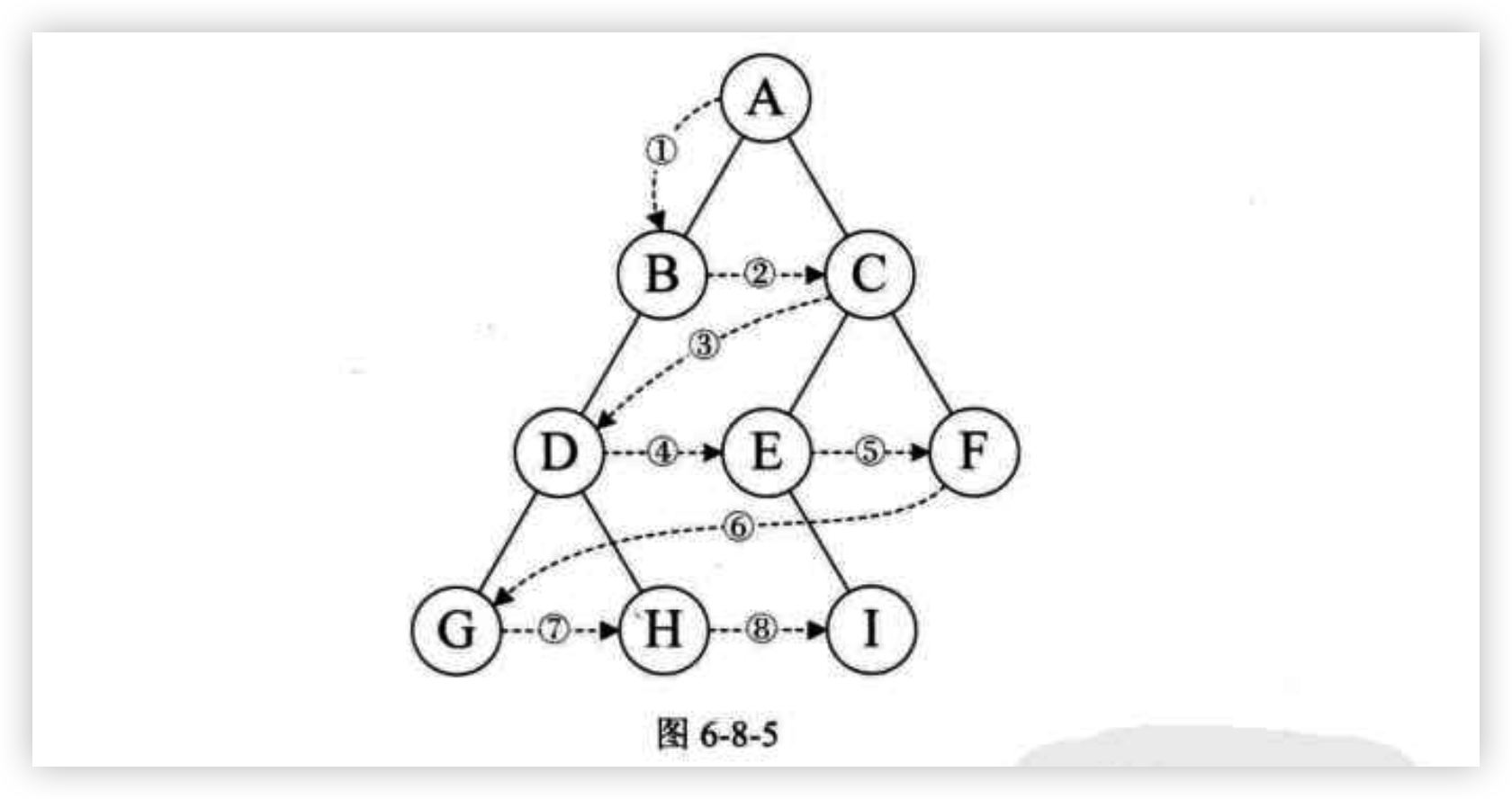
• 从根节点开始，一层一层的遍历
• 同一层，按从左到右的顺序