二叉树相关题

1.二叉树最大深度

思路：

如果节点为空 (root === null)，表示这一部分的深度是 0。

如果节点不为空，递归地计算左子树和右子树的深度，然后返回左右子树深度的最大值加上 1（表示当前节点的深度）

代码实现：

function maxDepth(root) {
    // 基本情况：如果节点为空，深度为 0
    if (root === null) return 0;
    
    // 递归计算左子树和右子树的深度
    let leftDepth = maxDepth(root.left);
    let rightDepth = maxDepth(root.right);
    
    // 返回左右子树深度的最大值 + 1（当前节点的深度）
    return Math.max(leftDepth, rightDepth) + 1;
}

2.判断是否是对称二叉树

对称二叉树 是一种二叉树，其左右子树是镜像对称的（所谓镜像对称，是指沿中线折叠后左右两边是相同的）

对称的二叉树

 

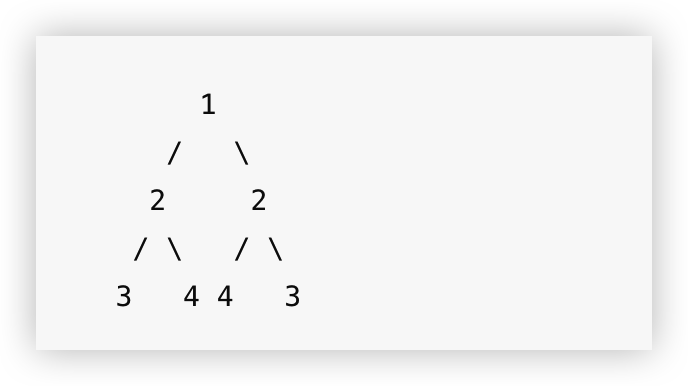
非对称的

 

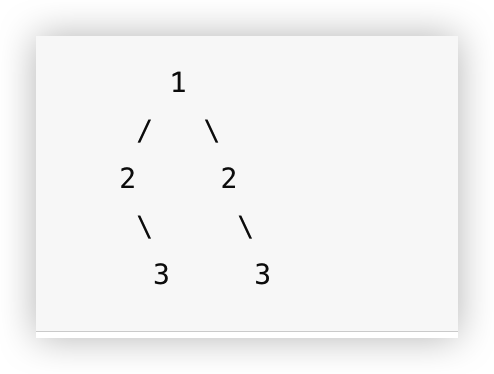
判断二叉树是否对称

一棵二叉树要是对称的，应当满足下面的条件：

1. 根节点左右子树的值相等。

2. 左子树的左子树与右子树的右子树对称。

3. 左子树的右子树与右子树的左子树对称。

function isSymmetric(root) {
    // 如果根节点为空，直接返回 true
    if (root === null) return true;

    // 定义递归函数判断两个树是否是镜像对称
    function isMirror(t1, t2) {
        // 如果两个节点都为空，返回 true
        if (t1 === null && t2 === null) return true;
        
        // 如果一个节点为空，另一个不为空，返回 false
        if (t1 === null || t2 === null) return false;
        
        // 判断当前节点值是否相等，并递归判断左子树和右子树的对称性
        return (t1.val === t2.val) &&
               isMirror(t1.left, t2.right) &&
               isMirror(t1.right, t2.left);
    }

    // 判断根节点的左右子树是否是镜像对称的
    return isMirror(root.left, root.right);
}

 测试代码：

// 定义二叉树节点
function TreeNode(val) {
    this.val = val;
    this.left = null;
    this.right = null;
}

// 创建一个对称的二叉树
let root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(2);
root.left.left = new TreeNode(3);
root.left.right = new TreeNode(4);
root.right.left = new TreeNode(4);
root.right.right = new TreeNode(3);

// 判断是否对称
console.log(isSymmetric(root));  // 输出 true

// 创建一个不对称的二叉树
let root2 = new TreeNode(1);
root2.left = new TreeNode(2);
root2.right = new TreeNode(2);
root2.left.right = new TreeNode(3);
root2.right.right = new TreeNode(3);

// 判断是否对称
console.log(isSymmetric(root2));  // 输出 false