图论-割点与割边(已被优化)

这是摘自算法书上的一篇 Tarjan 求割点算法

dfn[i] 代表时间戳数组
back[i] 代表该点 不依靠祖先节点 能回到的最远的祖先节点

采用链式前向星建图，结果存储在 iscut[ ] 数组中

---

点击查看代码

int head[N], cnt = 0;
struct Edge{
    int from, to, nxt;
}e[N << 1];
void add(int u, int v){
    e[++cnt].from = u;
    e[cnt].to = v;
    e[cnt].nxt = head[u];
    head[u] = cnt;
}

int dfn[N], back[N], tim; // dfn[i] 时间戳  back[i] 回退到祖先
bool iscut[N]; // 结果数组

void dfs(int u, int fa){
    dfn[u] = back[u] = ++tim;
    int child = 0;
    for(int i = head[u]; i != 0; i = e[i].nxt){
        int v = e[i].to;
        if(!dfn[v]){
            // v 没访问过
            child++;
            dfs(v, u);
            back[u] = min(back[u], back[v]);
            if(back[v] >= dfn[u] && u != 1)
                iscut[u] = true;
        }
        else if(dfn[v] < dfn[u] && v != fa){
            back[u] = min(back[u], dfn[v]); // 注意不是  back[v]
        }
    }
    if(u == 1 && child >= 2){
        iscut[u] = true;
    }
}

---

后来敲的时候，有一行代码为 back[u] = min(back[u], dfn[v]);容易误写为back[u] = min(back[u], back[v]
此时就要重视 back[ ] 表示 不依靠祖先节点

当然，这个稍微改动下，就是割边

---

点击查看代码

int head[N], cnt = 0;
struct Edge{
    int from, to, nxt;
}e[N << 1];
void add(int u, int v){
    e[++cnt].from = u;
    e[cnt].to = v;
    e[cnt].nxt = head[u];
    head[u] = cnt;
}

int dfn[N], back[N], tim; // dfs[i] 时间戳  back[i] 回退到祖先
bool iscut[N << 1]; // 结果数组

void dfs(int u, int fa){
    dfn[u] = back[u] = ++tim;
    int child = 0;
    for(int i = head[u]; i != 0; i = e[i].nxt){
        int v = e[i].to;
        if(!dfn[v]){
            // v 没访问过
            child++;
            dfs(v, u);
            back[u] = min(back[u], back[v]);
            if(back[v] > dfn[u] && u != 1)
                iscut[i] = true;  // 边为
        }
        else if(dfn[v] < dfn[u] && v != fa){
            back[u] = min(back[u], dfn[v]); // 注意不是  back[v]
        }
    }
    if(u == 1 && child >= 2){
        for(int i = head[u]; i != 0; i = e[i].nxt){
            iscut[i] = true;
        }
    }
}

---

至于这份割边代码，iscut数组记录的倒是有些奇怪，但也能输出边的信息

---

2024/5/10：补一张情况说明，借用了洛谷名为 wind_seeker 的一张图

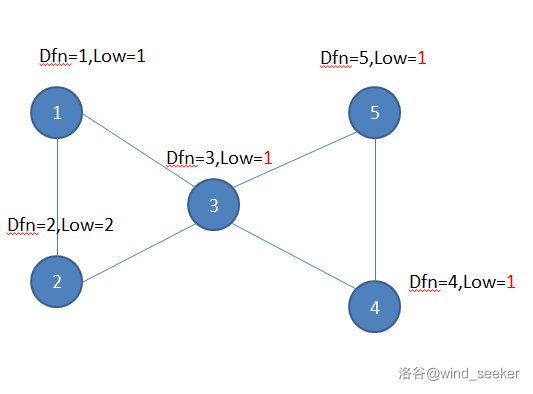
对此，我做出求割点（其实笔者感觉应该称为无向图的性质）的 back 数组概括:

本环境下，back[i]仅取决于自己与子节点（所有时间戳在自己之后且能联通的）能连接到祖先的能力
而与祖先节点连接到更祖先节点的能力无关

（我父亲厉害与我无关，但我儿子厉害与我有关）

---

2024.5.22 经过几天的点双，边双的思考后，优化了割点与割边的代码，使我更深入的理解了 Tarjan 算法，细节过多，新开两篇详细讲述