【logistic回归】原理目的 学习笔记

目的
 
在进入logistic回归模型原理介绍之前，我们先来考量一个其是想要解决什么样的问题。二元分类相信大家一定不会陌生，分类过程中其想要解决的问题是0/1的问题，我们把它称作Binary Classification，图像领域中解决的是某个东西是或不是的问题，但如果我想知道的是自信度（Probabilities of Classes）呢，也就是某个东西是人脸的概率。这种软分类（Soft Binary Classification）的情况下，当初用来解决线性回归的sign符号函数就不适用了，数学意义上理解符号函数并非是平滑的，因此解决这个问题的思路就变成了寻找一个函数形成【0,1】的映射，sigmoid函数出现了。
        

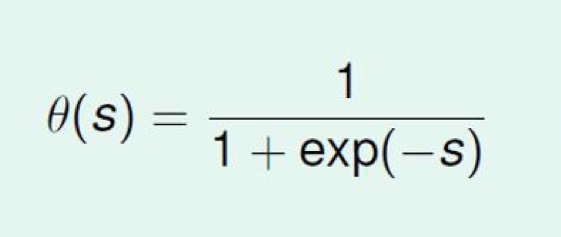
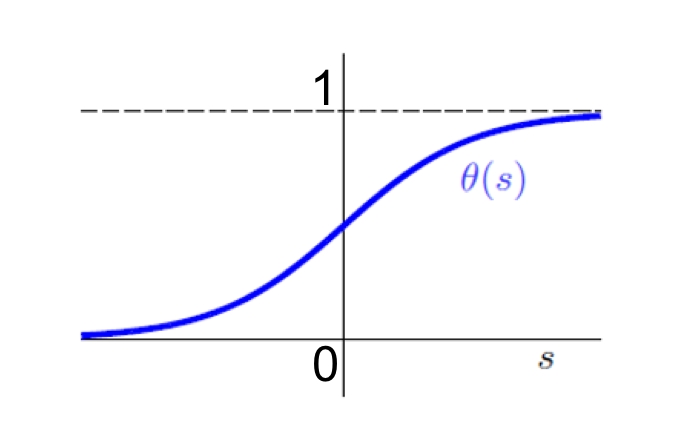
在这里，s=yn（wT）xn，其中yn为类别，wT为最终待求分类面法向量，xn为打好标记的数据集中的其中一个，刚好对应s=0时概率为50% 。
 
原理
 
在了解目的之后，现在待解决的问题就和线性回归问题很类似了，找到个合适的损失函数梯度下降法就完事了。 
线性回归的损失函数一般选择的是方差损失函数，但对于sigmoid函数却并不适用，一般采用的损失函数是交叉熵损失函数。交叉熵函数时信息论里用来表示信息集相似程度的一种方式，在回归模型里则具象为标记集分布和待求的sigmoid分布的交叉熵，（原理不再解释，可以参考交叉熵的定义），最后则化为下面这个函数：

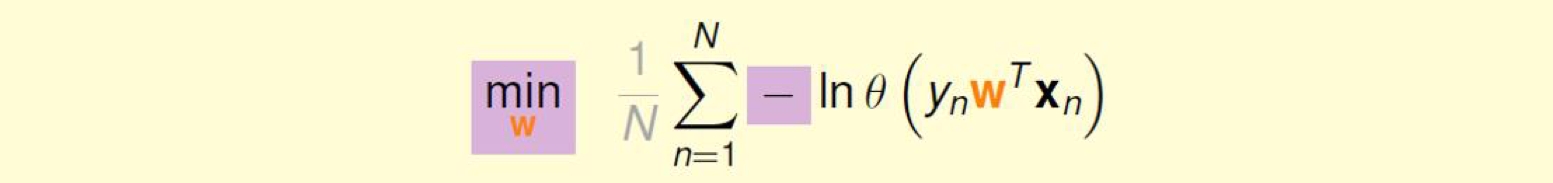
再之后，只需要求出交叉熵的梯度即可根据随机梯度下降法求解出最优 w ，可通过下面的式子给出最后表达式：
 

之后我们只需采用传统梯度下降法或者随机梯度下降法进行w的求解，只需进行迭代直到梯度为0。
 
 
 

方差vs交叉熵
 
问题到上面其实已经结束了，但笔者还想讨论一下为什么采用交叉熵损失函数而不是线性回归问题里采用的方差损失函数作为判断，这个过程可以通过对方差损失函数梯度值得分析给出：
假设我们采用方差损失函数作为判别依据，表达式：

则方差损失函数的梯度为：

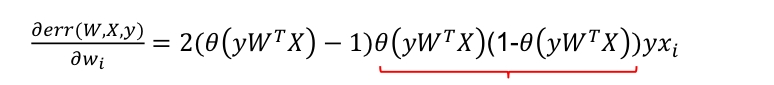
对照着sigmoid函数图计算后可以发现，其梯度值在分的特别好（s趋向于1）和分的特别差（s趋向于0）的时候梯度都趋向于零，这就意味着当分的特别差时可能需要花费很长的时间。
下面我们比较一下两种损失函数的梯度值：
 

 
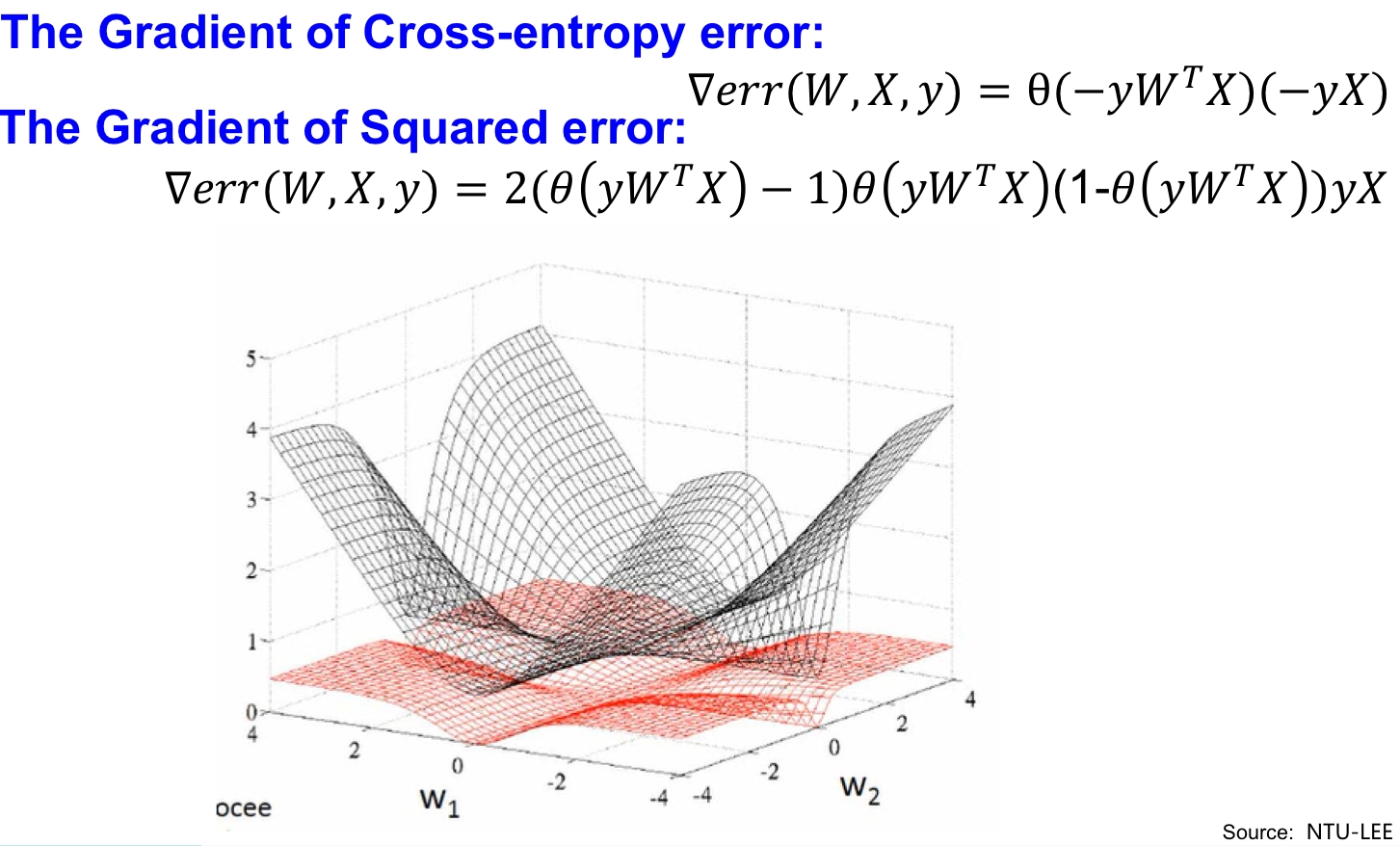
即当w1和w2非常类似或者非常不同时时，梯度都趋向于零，显然并不适合作为损失函数。