C4.5算法和K-means算法

C4.5 classification and K-means clustering(待更新）

C4.5分类算法

Algorithm

C4.5 builds decision trees from a set of training data in the same way as ID3, using the concept of information entropy. The training data is a set of already classified samples. Each sample consists of a p-dimensional vector , where the 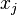represent attribute values or features of the sample, as well as the class in which falls.

At each node of the tree, C4.5 chooses the attribute of the data that most effectively splits its set of samples into subsets enriched in one class or the other. The splitting criterion is the normalized information gain (difference in entropy). The attribute with the highest normalized information gain is chosen to make the decision. The C4.5 algorithm then recurs on the smaller sublists.

This algorithm has a few base cases.

• All the samples in the list belong to the same class. When this happens, it simply creates a leaf node for the decision tree saying to choose that class.
• None of the features provide any information gain. In this case, C4.5 creates a decision node higher up the tree using the expected value of the class.
• Instance of previously-unseen class encountered. Again, C4.5 creates a decision node higher up the tree using the expected value.

Pseudocode

In pseudocode, the general algorithm for building decision trees is:^[3]

1. Check for base cases
2. For each attribute a
   1. Find the normalized information gain ratio from splitting on a
3. Let a_best be the attribute with the highest normalized information gain
4. Create a decision node that splits on a_best
5. Recur on the sublists obtained by splitting on a_best, and add those nodes as children of node

Implementations

J48 is an open source Java implementation of the C4.5 algorithm in the weka data mining tool.

 

 

 

K-means聚类算法

Description

Given a set of observations (x₁, x₂, …, x_n), where each observation is a d-dimensional real vector, k-means clustering aims to partition the n observations into k (≤ n) sets S = {S₁, S₂, …, S_k} so as to minimize the within-cluster sum of squares (WCSS) (sum of distance functions of each point in the cluster to the K center). In other words, its objective is to find:

where μ_i is the mean of points in S_i.

Algorithms

Standard algorithm

The most common algorithm uses an iterative refinement technique. Due to its ubiquity it is often called the k-means algorithm; it is also referred to as Lloyd's algorithm, particularly in the computer science community.

Given an initial set of k means m₁⁽¹⁾,…,m_k⁽¹⁾ (see below), the algorithm proceeds by alternating between two steps:^[7]

Assignment step: Assign each observation to the cluster whose mean yields the least within-cluster sum of squares (WCSS). Since the sum of squares is the squared Euclidean distance, this is intuitively the "nearest" mean.^[8] (Mathematically, this means partitioning the observations according to the Voronoi diagram generated by the means).

where each is assigned to exactly one , even if it could be assigned to two or more of them.

Update step: Calculate the new means to be the centroids of the observations in the new clusters.

Since the arithmetic mean is a least-squares estimator, this also minimizes the within-cluster sum of squares (WCSS) objective.

The algorithm has converged when the assignments no longer change. Since both steps optimize the WCSS objective, and there only exists a finite number of such partitionings, the algorithm must converge to a (local) optimum. There is no guarantee that the global optimum is found using this algorithm.

The algorithm is often presented as assigning objects to the nearest cluster by distance. The standard algorithm aims at minimizing the WCSS objective, and thus assigns by "least sum of squares", which is exactly equivalent to assigning by the smallest Euclidean distance. Using a different distance function other than (squared) Euclidean distance may stop the algorithm from converging.^{[citation needed]} Various modifications of k-means such as spherical k-means and k-medoids have been proposed to allow using other distance measures.

Initialization methods

Commonly used initialization methods are Forgy and Random Partition.^[9] The Forgy method randomly chooses k observations from the data set and uses these as the initial means. The Random Partition method first randomly assigns a cluster to each observation and then proceeds to the update step, thus computing the initial mean to be the centroid of the cluster's randomly assigned points. The Forgy method tends to spread the initial means out, while Random Partition places all of them close to the center of the data set. According to Hamerly et al.,^[9] the Random Partition method is generally preferable for algorithms such as the k-harmonic means and fuzzy k-means. For expectation maximization and standard k-means algorithms, the Forgy method of initialization is preferable.

• Demonstration of the standard algorithm
• 

  1. k initial "means" (in this case k=3) are randomly generated within the data domain (shown in color).

• 

  2. k clusters are created by associating every observation with the nearest mean. The partitions here represent the Voronoi diagram generated by the means.

• 

  3. The centroid of each of the k clusters becomes the new mean.

• 

  4. Steps 2 and 3 are repeated until convergence has been reached.

As it is a heuristic algorithm, there is no guarantee that it will converge to the global optimum, and the result may depend on the initial clusters. As the algorithm is usually very fast, it is common to run it multiple times with different starting conditions. However, in the worst case, k-means can be very slow to converge: in particular it has been shown that there exist certain point sets, even in 2 dimensions, on which k-means takes exponential time, that is 2^Ω(n), to converge.^[10] These point sets do not seem to arise in practice: this is corroborated by the fact that the smoothed running time of k-means is polynomial.^[11]

The "assignment" step is also referred to as expectation step, the "update step" as maximization step, making this algorithm a variant of the generalized expectation-maximization algorithm.

 

参考资料：

http://www.cs.umd.edu/~samir/498/10Algorithms-08.pdf

https://en.wikipedia.org/wiki/K-means_clustering

http://www.cnblogs.com/zhangchaoyang/articles/2842490.html