[斯坦福2025春季新课CS336：从头开始构建大模型]自学笔记（1-4）

大模型概述与Tokenization & 利用Pytorch搭建大模型

Tokenizer

BPE (byte pair encode)

• 从字符级别开始，逐步合并高频的字符对。
• 最终生成一个既能表示常见单词，又能拆解未知词的子词词汇表 。
• 可以有效控制词汇表大小，同时避免“未登录词”问题（OOV, Out-of-Vocabulary）。

参考文献

在学习 BPE merges 时，初始符号集合（字符 / 字节）是固定保留的。每次 merge 新增一个复合符号（subword），旧符号不会从词表中移除。例如：

1. 原始 token："h" → id 10；"e" → id 11
2. merge("h","e") → "he" → id 502

其他类型的tokenizer

• Character-based tokenization：以单个字符为最小单元，序列长度较长，建模效率较低，但不存在 OOV 问题。
• Byte-based tokenization：以 UTF-8 字节为基本单元，可表示任意文本，不存在 OOV，但非 ASCII 字符会被拆分为多个字节，导致序列较长。
• Word-based tokenization：将文本按空格或规则切分为词级单元，词表规模大，OOV 问题严重，已较少用于现代神经网络模型。把字符串分割为字符串序列

Scaling Law

是机器学习领域描述模型性能与模型规模、训练数据集大小及计算资源之间可预测关系的经验性规律，被业界视为大模型预训练的核心原则

它指出模型的损失（损失越小模型性能越好）主要由模型大小和数据量共同决定

用于指导模型设计，避免“越大越好”的误区，根据计算量合理分配模型大小和数据量

指导如何在给定计算量下，直线最优配比

数据类型

类型	符号位	指数位	尾数位
FLOAT32	1	8	23
FLOAT16	1	5	10
BF16	1	8	7

torch的view操作

torch中view操作创建视图和引用，不会复制数据，如果对tensor执行transpose，会导致contiguous属性变为False，需要调用contiguous()方法来生成一个新的连续tensor才能进行view操作。

前向传播/反向传播计算量

前向传播

\[\text{FLOPS}_\text{forward} = N_\text{tokens} \times 2\times N_\text{params} \]

反向传播

\[\text{FLOPS}_\text{backward} = 2\times\text{FLOPS}_\text{forward} \]

因为反向传播需要计算\(\frac{\partial L}{\partial W}\)和\(\frac{\partial L}{\partial X}\)

• Q：为什么要计算X的梯度？
• A：因为根据链式法则，计算上一层W的梯度需要上一层的输出，也就是此处的X

训练总的FLOPS：

\[\text{FLOPS}_\text{train} = \text{FLOPS}_\text{forward} + \text{FLOPS}_\text{backward} = 6\times N_\text{tokens} \times N_\text{params} \]

大模型架构设计与超参数调优

Pre-norm

只有早期的transformer使用post-norm，现在的LLM都是用pre-norm，因为效果更好（BLEU更高、Loss下降更快更小）

• Q：为什么残差连接在layer norm之外？
• A：残差连接提供了恒等映射，如果加入layer norm会破坏梯度传播特性

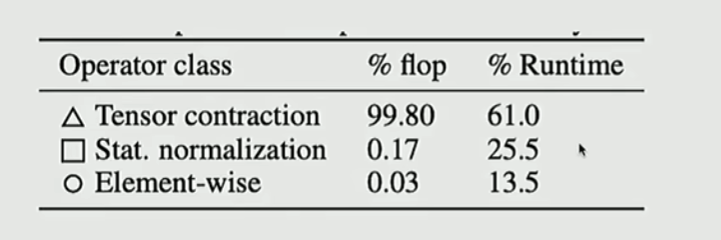
softmax, layer norm等归一化操作占的计算量少，但是耗时高，主要原因是计算统计量是访问内存频繁、效率低

FFN层

FFN层抛弃了偏置，只保留了矩阵乘法：

1. 减少参数量
2. 使训练更稳定（基于实验现象 ）

现在LLM常用GeGLU和SwiGLU作为FFN层中间的激活函数

激活函数

GELU（Gaussian Error Linear Unit，高斯误差线性单元）

定义为：

\[\text{GELU}(x) = x \cdot \Phi(x) \]

其中\(\Phi\)是标准高斯分布的累计分布函数

GLU（Gated Linear Unit，门控线性单元）

定义为：

\[\text{GLU}(x) = (W_a x) \odot \sigma(W_b x) \]

其中\(\odot\)表示逐元素相乘，\(\sigma\)是sigmoid函数。式中第二项作为门控机制，控制第一项的信息流动。\(W_a,\ W_b\)是激活函数中可学习的权重矩阵。

有的地方写成：

def glu(x):
    assert x.shape[-1] % 2 == 0, "输入数组的最后一个维度必须是偶数"
    half_dim = x.shape[-1] // 2
    return x[..., :half_dim] * sigmoid(x[..., half_dim:])

看上去没有了可学习的参数，实际上是把参数投影后的结果concatenate在一起了传进来

其他

• Swish（pytorch中现在叫SiLU）和GLU很相似，但是没有可学习的权重矩阵：

\[\text{Swish}(x) = x \odot \sigma(x) \]

• GeGLU：GELU-based GLU

\[\text{GeGLU}(x)=(W_a x) \odot \text{GELU}(W_b x) \]

• SwiGLU：Swish-based GLU

\[\text{SwiGLU}(x)=(W_a x) \odot \text{Swish}(W_b x) \]

如果FFN的激活函数改为GLU/GeGLU/SwishGLU，会将\(d_{ff}\)改为原来的2/3（\(d_{ff}=\frac{8}{3}d_\text{model}\)），以保持参数量与计算量不变。

超参数设置

为什么\(d_{ff}\)通常设置为\(4*d_{model}\)？

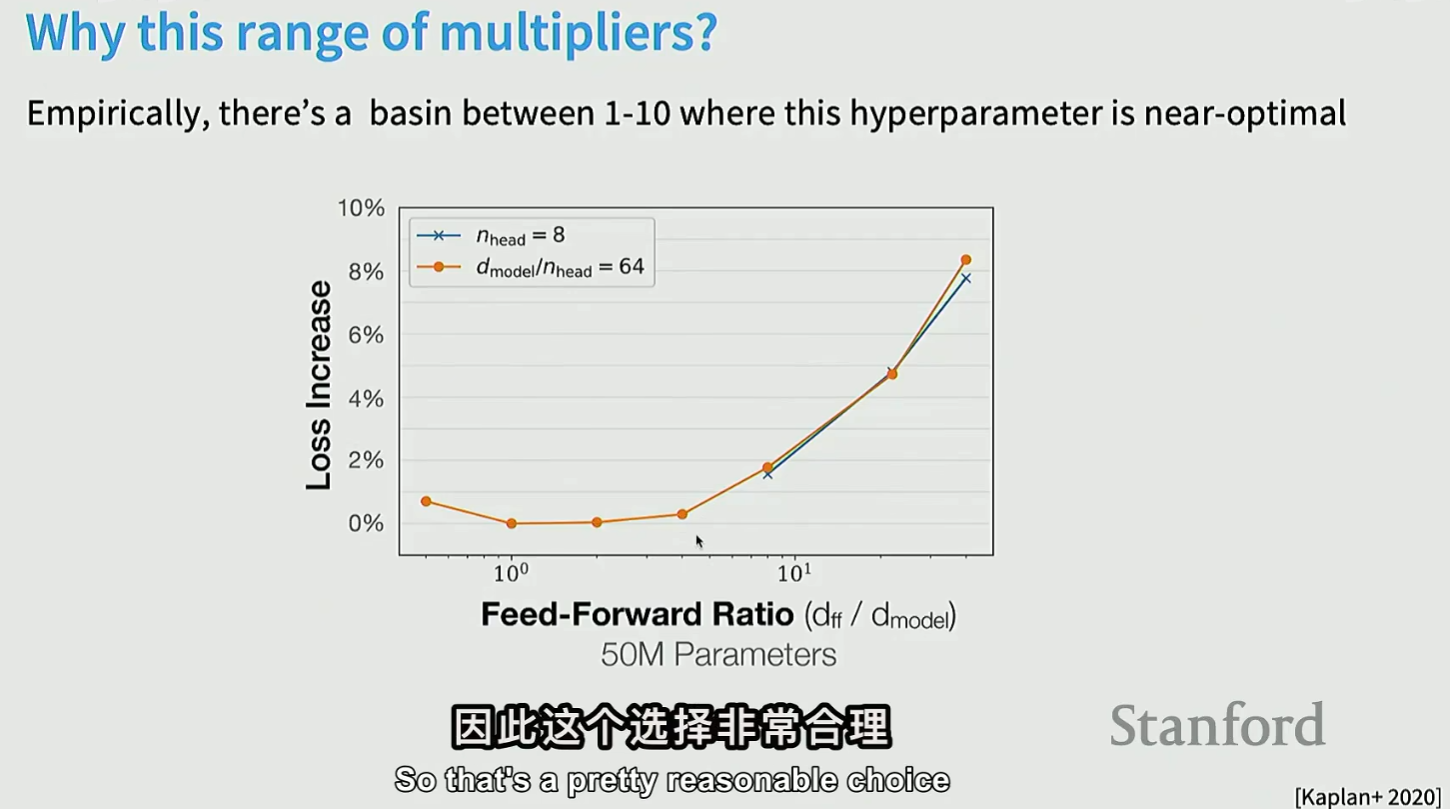
实验发现，在最优区间中4最靠近最优解，损失增加最少

困惑度(perplexity，PPL)

模型在预测下一个 token 时，平均有多少种“同样可能的选择”

• 困惑度越低：模型越“确定”，预测越准确
• 困惑度越高：模型越“困惑”，预测越差

例如：

• PPL = 10：模型平均相当于在 10 个候选 token 中随机选
• PPL = 100：模型几乎“蒙的”

PPL的计算与交叉熵很相似，交叉熵：

\[\mathcal{L}=-\frac{1}{T} \sum_{t=1}^{T} \log p(x_t \mid x_{<t}) \]

困惑度：

\[\text{PPL}= \exp(\mathcal{L})= \exp\left(-\frac{1}{T} \sum_{t=1}^{T} \log p(x_t \mid x_{<t})\right) \]

其他

• Q：大模型为什么用dropout较少？
• A：因为过程中预训练大多数是1个epoch，不会过拟合

• Q：什么是稀疏attention？
• A：为了减少KV的访存开销，可以让q关注部分k-v对（一般是相邻的部分），这被称为稀疏attention（sparse attention）

详解MOE架构

MOE选择token的策略

1. token被选择（token choice），每个token选择top-k个专家
2. expert被选择（expert choice），每个专家选择top-k个token，这种有益于专家负载均衡
3. token和expert双向选择

大多数work选择第一种

如何平衡experts之间的负载

Deepseek的MOE

• 把单个expert拆成若干个小的expert，增加数量但是整体参数量不变。缺点：涉及的专家很多，增加通信成本。解决方法：先选出m个设备，再在m个设备上选出k个expert
• 设置共享的expert

MOE负载均衡

如何避免expert极化，使用balance loss：

\[\mathrm{loss}=\alpha\cdot N\cdot\sum_{i=1}^{N}f_{i}\cdot P_{i} \]

\(N\)为expert数量，\(f_i\)为第\(i\)个expert被分配的token占比

\[f_{i}=\frac{1}{T}\sum_{x\in\mathcal{B}}\mathbb{1}\{\operatorname{argmax}p(x)=i\} \]

\(P_i\)为第\(i\)个expert被选择的概率占比

\[P_{i}=\frac{1}{T}\sum_{x\in\mathcal{B}}p_{i}(x). \]

如果考虑到GPU设备间的负载均衡，\(i\)可以表示设备编号

还有一种更简单的平衡方式：

\[g_{i,t}^{\prime}=\begin{cases}s_{i,t},&s_{i,t}+b_{i}\in\mathrm{Topk}(\{s_{j,t}+b_{j}|1\leqslant j\leqslant N_{r}\},K_{r}),\\0,&\mathrm{otherwise}.&\end{cases} \]

• 在线学习一个参数\(b_i\)，观察expert被分配的token：如果一个experts不受欢迎，增加\(b_i\)，反之减少\(b_i\)
• \(s_{i,t}\)：softmax score
• \(g_{i,t}^{\prime}\)：token \(t\) 分配给 expert \(i\) 时，该 expert 对该 token 的贡献权重

如何稳定训练MOE

使用Z-loss：

\[L_{z}(x)=\frac{1}{B}\sum_{i=1}^{B}\left(\log\sum_{j=1}^{N}e^{x_{j}^{(i)}}\right)^{2} \]

\(B\)表示token数量，\(N\)表示expert数量，\(x\)为logits。MOE训练的不稳定来自router，Z-loss目的是惩罚logits过大

• Q：为什么sampling的时候 temperature=0，还是存在不一致的结果？
• A：一种原因：MOE路由选择的引发了随机性：当一个batch内涌入某一expert专家过多，导致部分token被drop，从而导致了不同的结果

Upcycle

核心思想：利用已经训练好的 dense FFN 权重，来初始化 MoE 中的各个 expert（而不是从随机初始化开始）。对于Router，通常是随机初始化或接近均匀分配。

为什么不会一直“塌缩成一个 dense FFN”？

• routing 是 token-level 的；
• 负载均衡 loss / auxiliary loss 会鼓励 expert 使用均衡；

因此，即使 experts 参数完全相同，不同 token 的 routing 会不同，从而在反向传播中逐渐让 experts 分化（specialization）。