[NeurIPS2024]Breaking Long-Tailed Learning Bottlenecks A Controllable Paradigm with Hypernetwork-Generated Diverse Experts

这篇论文提出使用超网络生成专家模型的参数，实现可控的、能根据用户偏好预测的专家模型。

Related works

长尾学习（long-tailed learning）的方法包括重采样、设计损失函数，旨在提高尾部类的表现。然而，这类方法往往假设测试集是类别平衡的，在训练时的操作也是希望学到一个均衡预测分类的模型。这在实际场景中，并不能很好的处理训练和测试的域转移（domain shift）问题。

近几年，多专家的长尾学习被提出。在多专家网络中，共用一个特征提取器，用多个（一般是3个）线性层表示专家模型。专家网络有着较强的分布适应能力，因为不同的专家可以通过不同的损失函数学习不同分布的类别。大部分长尾多专家工作使用3个专家，分别是：

• 前向专家（the forward expert），模拟原始的长尾分布

\[\mathcal{L}_\text{ce}=\frac{1}{n_s}\sum_{x_i\in\mathcal{D}_s}-y_i\log\sigma(v_1(x_i)) \]

• 均匀专家（the uniform expert），通过logit adjustment，用先验对数减少头部类的logits

\[\mathcal{L}_\text{bal}=\frac{1}{n_s}\sum_{x_i\in\mathcal{D}_s}-y_i\log\sigma(v_2(x_i)+\log\pi) \]

• 后向专家（the backward expert ），使用逆softmax 损失（inverse softmax loss），通过逆先验的对数增加尾部类的logits

\[\mathcal{L}_\text{bal}=\frac{1}{n_s}\sum_{x_i\in\mathcal{D}_s}-y_i\log\sigma(v_2(x_i)+\log\pi) \]

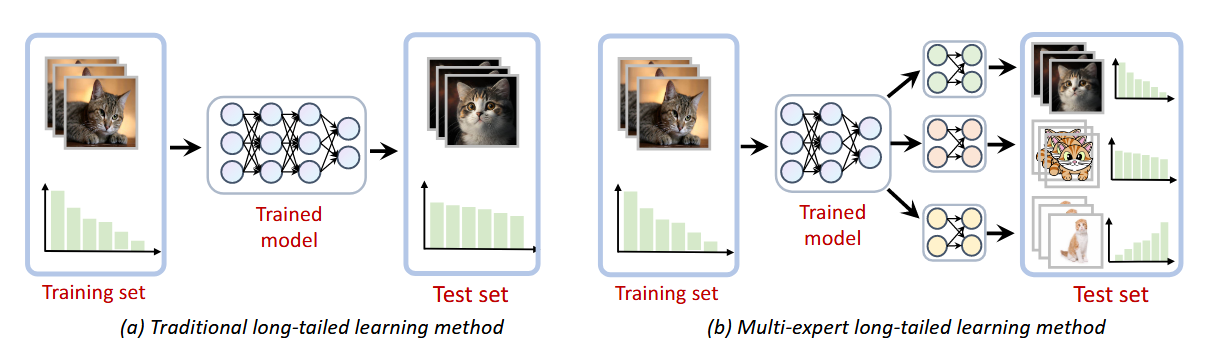
几个多专家长尾学习的代表工作

Long-tailed Recognition by Routing Diverse Distribution-Aware Experts. ICLR 2021

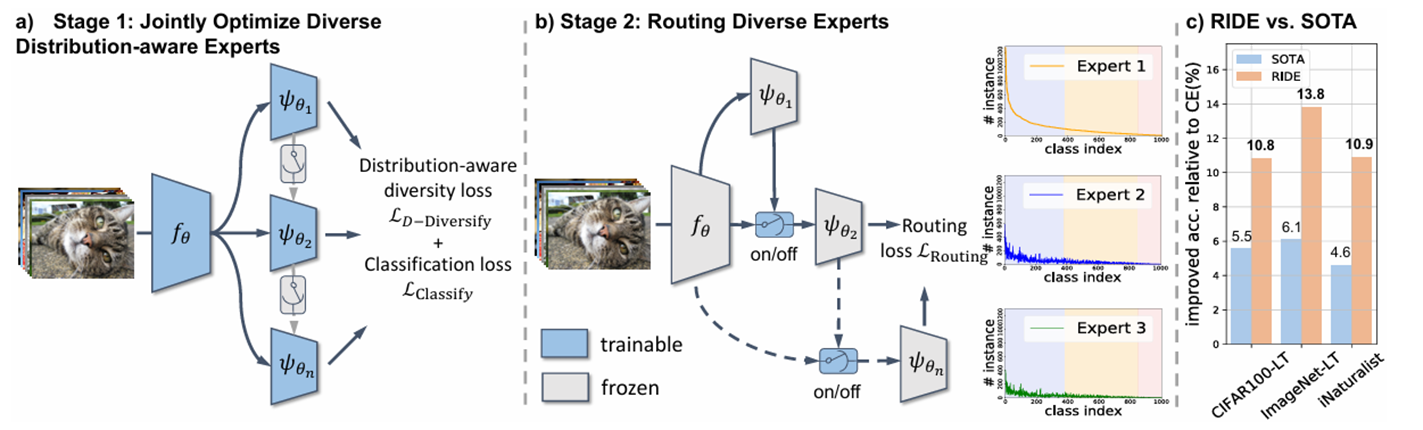
这篇文章提出了RIDE（Routing Diverse Distribution-Aware Experts），除了训练特征提取器和多专家，还在引入了2阶段训练，在2阶段训练上，训练了路由模块。模型会对难分类的样本动态地分配专家，头部类参与的专家少，尾部类参与的专家多。

Self-supervised aggregation of diverse experts for test-agnostic long-tailed recognition. NeuraIPS 2022

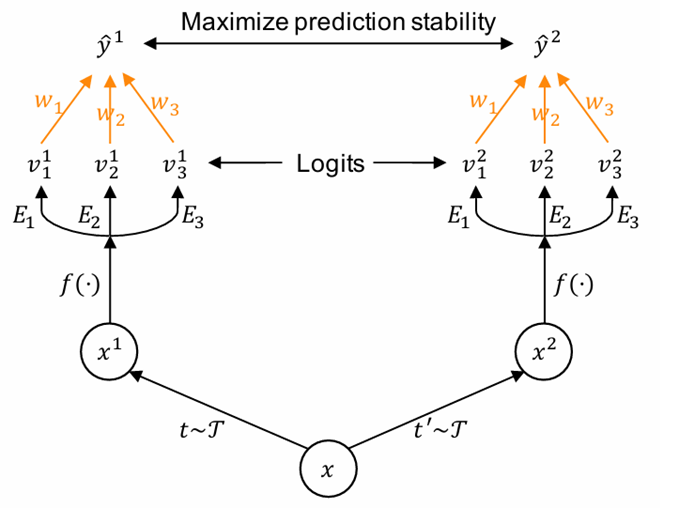
这篇文章提出了SADE（Self-supervised Aggregation of Diverse Experts）。作者基于假设和观察：专家对于在它们擅长的类别上，对于不同视角的样本应该有着稳定的预测结果，例如，尾部类专家对于使用不用图像增强的尾部类样本应该有着一致的预测结果。因此，就可以把测试集当成无标签数据，作自监督训练，更新参数\(w_1\ w_2,\ w_3\)，去学习测试集的分布，缓解训练集和测试集的域偏移

Introduction

本文中，作者指出，这些长尾的方法关注的是整体的分类性能表现。然而，在某些情况下，用户需要对头部类或尾部类有一定偏好。例如：

• 对于肺癌，大多数图片是正常图片，用户会愿意提高假阳率去实现对尾部类的召回，保证不会遗漏病患。
• 对于自然保护区，用户更关注主要物种，实现种群数量的准确统计。

在本文中，作者就提出一种可控的多专家长尾学习方法，它在单一的数据集上训练，并能根据用户偏好，在不同分布的测试集上进行分类。

一些简单的证明

对比单网络的长学习经验风险：

\[R_{test}(f)=R_m(f)+\sum_{i=1}^K(\pi_i^{test}-\pi_i^m)\cdot\mathbb{E}_{\boldsymbol{x}\sim P_{test}(\boldsymbol{x}|y=i)}[\ell(f(\boldsymbol{x};\boldsymbol{\theta}),i)] \]

多专家长尾学习的经验风险可表示为：

\[R_{test}(\hat{f})\leq\frac{1}{N}\sum_{m=1}^{N}R_{m}(f_{m})+2M\cdot\left(\frac{1}{N}\sum_{m=1}^{N}\delta(\mathcal{E}_{m},\mathcal{E}_{test})+\frac{N-1}{N}\Delta(\mathcal{E}_{1},\ldots,\mathcal{E}_{N})\right) \]

其中\(M=\operatorname*{max}_{i,\boldsymbol{x}}\ell(\hat{f}(\boldsymbol{x}),i)\)，\(\mathcal{E}\)表示专家训练/测试环境，\(\delta(\mathcal{E}_i,\mathcal{E}_j)=\frac{1}{2}\sum_{k=1}^K|\pi_k^i-\pi_k^j|\)表示两个环境变异距离， \(\Delta(\mathcal{E}_{1},\ldots,\mathcal{E}_{M})=\operatorname*{max}_{i,j\in\{1,\ldots,M\}}\delta(\mathcal{E}_{i},\mathcal{E}_{j})\)表示环境总变异距离（Environment’s Total Variation Distance，ETVD）。

多专家长尾学习的经验风险有3项组成：

1. 所有专家的平均经验风险
2. 训练环境与测试环境之间的平均总变异距离。
3. 训练环境之间的 ETVD 加权平均值。

多专家方法可以捕捉不同环境的分布特征，从而减少训练环境与测试环境之间的分布差异

Method

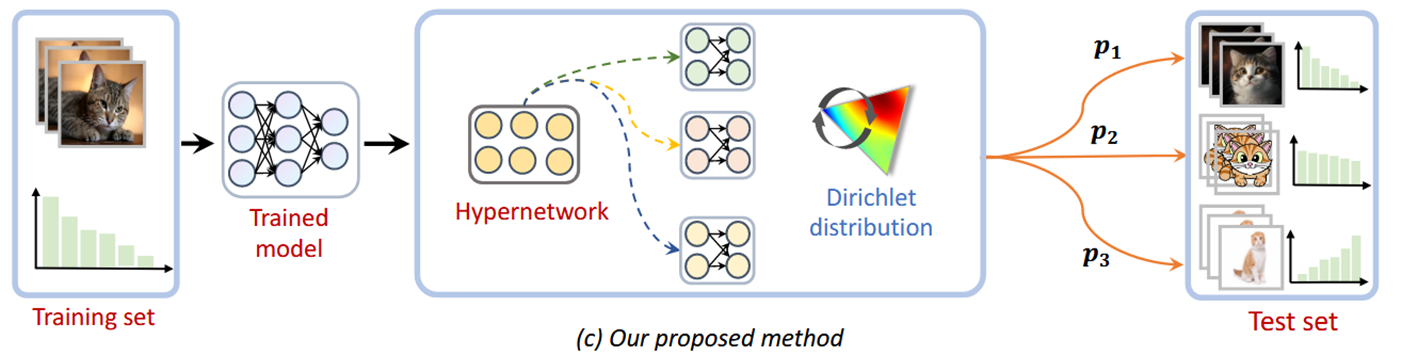
狄利克雷分布可以很好地对这种多类别比例的不确定性进行建模。它能够生成一组符合概率分布的主题比例向量，这些向量可以表示文本中各个主题的相对重要性。并且通过狄利克雷分布的性质，可以对文本的主题结构进行有效的学习和推断，发现文本集合中的潜在主题模式。

模型组成：

\[f_i(\mathbf{x})=g_{w_i}(\phi_\theta(\mathbf{x})),\quad i=1,\ldots,T \]

\(\phi_\theta\)表示特征提取器，\(g_{w_i}\)表示专家模型，区别于之前的方法，作者的专家模型通过超网络（hypernetwork）生成。超网络是一个生成专家模型参数的网络，它的输入是一个随机向量，输出是一个专家模型的参数。这样，就可以通过调整输入的随机向量，生成不同的专家模型：

\[\mathbf{w}_i=h_\psi(\hat{\boldsymbol{r}}_i),\quad i=1,\ldots,T \]

超网络的输入为\(\hat{\boldsymbol{r}}_i=\frac{\boldsymbol{r}\odot\boldsymbol{\alpha}_i}{\boldsymbol{r}^\top\boldsymbol{\alpha}_i}\)，其中\(\boldsymbol{r}\)是一个可训练的偏好向量长度为\(T\)，\(\boldsymbol{\alpha}_i\)是一个采样于狄利克雷分布的随机噪声\(\boldsymbol{\alpha}_i\sim\mathrm{Dir}(\boldsymbol{\beta}_i),\ \boldsymbol{\beta}_i\in\mathbb{R}_+^T\)

通过调整迪利克雷分布参数，可以生成不同的专家模型：

• \(\beta_1>\beta_2=\beta_3\) simulate the long-tailed distribution.
• \(\beta_1=\beta_2=\beta_3\) simulate the uniform distribution.
• \(\beta_1<\beta_2=\beta_3\) simulate the inverse long-tailed distribution.

最后的损失函数表示为：

\[\min_{\boldsymbol{\Theta}}\left(\sum_{i=1}^T\mathcal{L}_i(\boldsymbol{\Theta},\mathcal{D})+\lambda\cdot\log\sum_{i=1}^T\exp\left(\frac{1}{\lambda}\mathcal{L}_i(\boldsymbol{\Theta},\mathcal{D})\right)\right) \]

其中第二项是一个平滑切比雪夫标量化正则项，作者是直接使用了 “Smooth Tchebycheff scalarization for multi-objective optimization ICLR. 2024.
”的结论。

在测试阶段，噪声\(\boldsymbol{\alpha}\)不再来自迪利克雷分布，而是由用户输入\(\boldsymbol{\alpha}^*=(\alpha_1^*,\alpha_2^*,\alpha_3^*)^\top\)同样，再与\(\boldsymbol{r}=(r_1,r_2,r_3)^\top\)计算：\(\hat{\boldsymbol{r}}=\frac{\boldsymbol{r}\odot\boldsymbol{\alpha}^*}{\boldsymbol{r}^\top\boldsymbol{\alpha}^*}\)

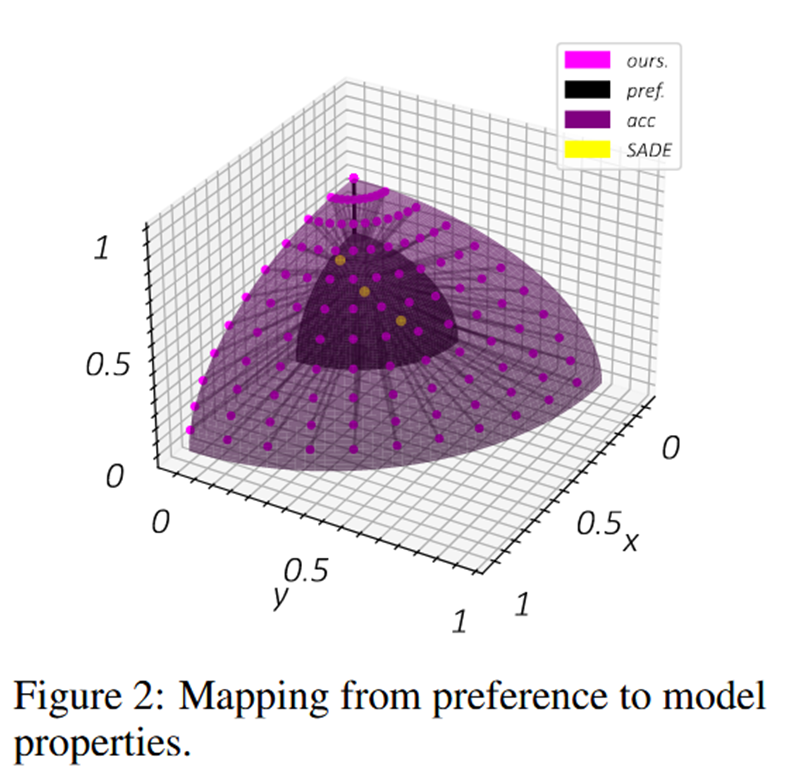
这张图中，坐标轴有两层意思，深色表示偏好向量的值空间；浅色表示不同分布下的分类准确率。作者可以通过偏好向量在不同分布下取得不同的偏好结果，所以可以到达平面任意点，而黄色的baseline只能局限于部分。

实验结果

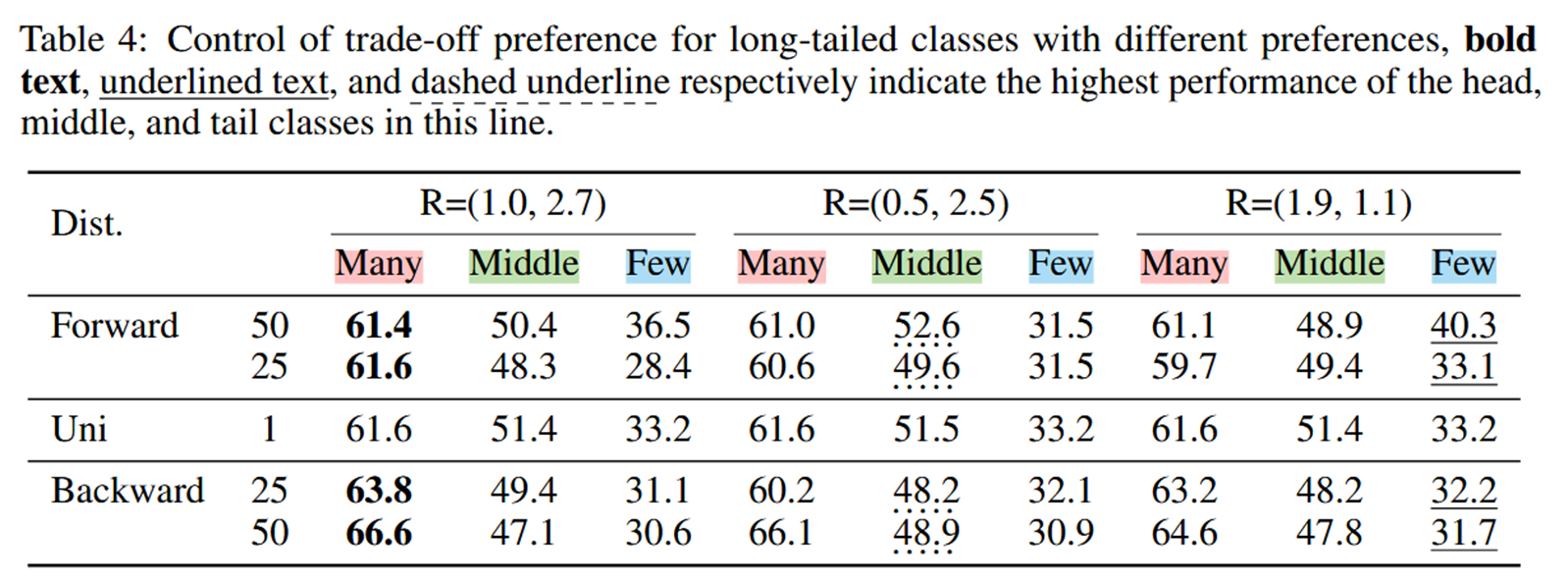
作者用极坐标R表示用户的偏好向量（不知道咋换算的），从结果上来看提升还是非常有限的

参考文献

• Xudong Wang, Long Lian, Zhongqi Miao, Ziwei Liu, Stella X. Yu: Long-tailed Recognition by Routing Diverse Distribution-Aware Experts. ICLR 2021
• Zhang, Yifan, et al. "Self-supervised aggregation of diverse experts for test-agnostic long-tailed recognition." Advances in neural information processing systems 35 (2022): 34077-34090.
• Lin, Xi, et al. "Smooth Tchebycheff scalarization for multi-objective optimization." Proceedings of the 41st International Conference on Machine Learning. 2024.
• Zhao, Zhe, et al. "Breaking Long-Tailed Learning Bottlenecks: A Controllable Paradigm with Hypernetwork-Generated Diverse Experts." The Thirty-eighth Annual Conference on Neural Information Processing Systems.