Python实验3 函数与代码复用

实验目的：理解函数封装与递归思想
实验任务：

1. 基础 ：编写函数 cal_factorial(n)计算阶乘（循环实现）。

点击查看代码

def cal_factorial(n):
    if n < 0:
        return "输入错误，阶乘仅对非负整数定义"
    result = 1
    for i in range(1, n + 1):
        result *= i
    return result

# 测试阶乘函数
print(cal_factorial(5))  # 输出 120

2. 进阶 ：用递归实现斐波那契数列（考虑添加缓存优化）。
使用字典memo作为缓存来存储已经计算过的斐波那契数，避免重复计算。

点击查看代码

def fibonacci(n, memo={}):
    if n in memo:
        return memo[n]  #缓存存储已经计算过的斐波那契数
    if n <= 1:
        return n
    memo[n] = fibonacci(n - 1, memo) + fibonacci(n - 2, memo)
    return memo[n]

# 测试斐波那契数列函数
print(fibonacci(10))  # 输出 55

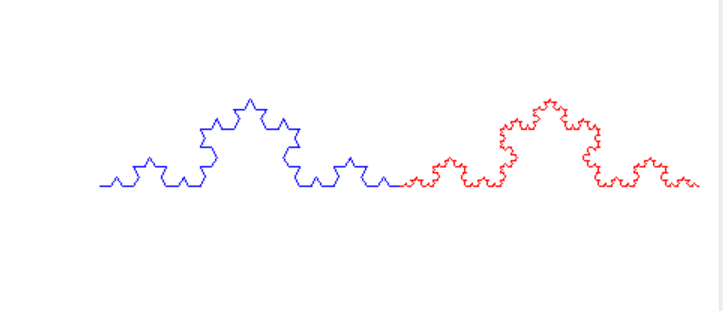
3. 拓展 ：科赫曲线正向、反向绘制，加入绘制速度、绘制颜色等额外功能

点击查看代码

import turtle


def koch_curve(t, order, length, angle=60):
    if order == 0:
        t.forward(length)
    else:
        length /= 3.0
        koch_curve(t, order - 1, length)
        t.left(angle)
        koch_curve(t, order - 1, length)
        t.right(2 * angle)
        koch_curve(t, order - 1, length)
        t.left(angle)
        koch_curve(t, order - 1, length)


def draw_koch(t, order, length, color, direction):
    t.color(color)
    t.penup()
    t.goto(direction[0], direction[1])
    t.pendown()
    t.setheading(0)
    koch_curve(t, order, length)
    t.hideturtle()


def main():
    window = turtle.Screen()
    window.bgcolor("white")
    window.title("Koch Curve")

    t1 = turtle.Turtle()
    t2 = turtle.Turtle()

    # 设置绘制速度
    t1.speed(1)
    t2.speed(1)

    # 绘制正向科赫曲线
    draw_koch(t1, 3, 200, "blue", (-100, -100))

    # 绘制反向科赫曲线
    draw_koch(t2, 4, 200, "red", (100, -100))

    window.mainloop()


if __name__ == "__main__":
    main()

提示 ：递归函数需注意终止条件，避免栈溢