度的数量

code（记忆化搜索）

#include<iostream>
#include<cstring>
using namespace std;
const int N = 35;//因为Y最大为2的31次方,所以要尽量开比31大 

int dp[N][N],a[N],k,b,len;
int dfs(int pos,int cnt,int limit){//pos代表第几位数,cnt代表1的个数,limit代表是否有限制 
	if(!pos) return cnt==k;//
	if(!limit&&dp[pos][cnt]!=-1) return dp[pos][cnt];//没有限制且dp数组被访问过 
	int res = 0,up = limit ? a[pos] : b-1;//res为方案个数,up代表上界 
	for(int i = 0;i <= up;i++){
		if((i==1&&cnt==k) || i > 1) continue;
//(条件判断)当此位为1且1的个数满足题目所给k或此位数字大于1 
		res += dfs(pos-1,cnt+(i==1),limit&&i==up);
	} 
	return limit?res:dp[pos][cnt] = res;
	//有限制直接返回方案数,无限制更新数组dp 
}
int cal(int x)
{
	memset(dp,-1,sizeof(dp));//初始化dp数组为-1 
	len = 0;//记录转换为某进制的位数 
	while(x){
		a[++len] = x%b;
		 x/=b;
	}
	return dfs(len,0,1);
}
int main(){
	int l,r;
	cin>>l>>r>>k>>b;
	cout<<cal(r)-cal(l-1)<<endl;
	return 0;
}

递推方法
在分析之前，了解一个组合数递推公式

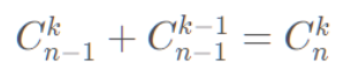
分析过程

• 第一步：将数x转化为B进制，记为N，将转化后的B进制数中的每一位存入一个nums数组

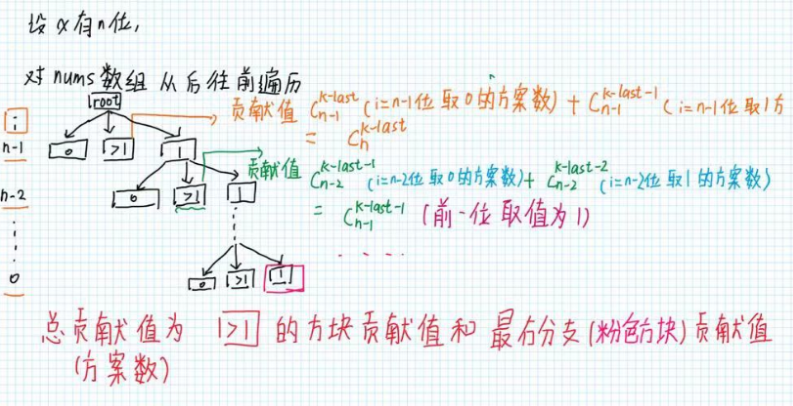
• 第二步：在nums数组中从高位到低位依次进行分类讨论，对于第i位数字x有3种情况（k含义见题意，last表示第i位之前的所有位取过的1的个数）

  • ① x = 0，此时第i位只能取0，不影响1的个数，贡献值为0，后面所有位（共i位，因为下标从0开始）可取k-last个1，直接讨论后面i位即可

  • ② x = 1：此时可以取0或1，当第i位取0时，后面i位都可以随意取值，可取k-last个1，
    当取1的时候，后面i位要在小于题目给定数（k）的前提下取值，在进行讨论，后面i位不能随便取，也就不是组合数（只能取k-last-1个1）

  • ③ x > 1：则i位上可取1，0，并且后面 i 位可以随意取k-last-1个1，除了0、1，其他值都不能取，其他值不符合题意

  图表结合

预处理f[i][j]表示从剩下i位，选择j个1的方案数，那么在（i，j）这个状态，
对于第i位，填1的话，那么接下来的状态为f[i-1][j-1]，
对于第i位，填0的话，那么接下来的状态就是f[i-1][j]，那么状态转移方程为f[i][j] = f[i-1][j] + f[i-1][j-1] ，
而初始状态即j=0，f[i][0] = 1（好好理解）

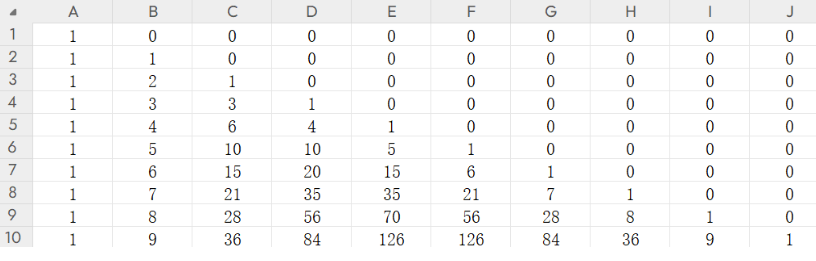
eg.预处理过程如下所示

dp（n）求出0~n上的满足题意的方案数

#include<iostream>
#include<vector>
using namespace std;
int k,B;
const int N= 35;
int f[N][N];
void init(){//求组合数 
	for(int i=0;i<N;i++){
		for(int j = 0;j<=i; j++){
			if(!j) f[i][j] = 1;
			else f[i][j] = f[i-1][j] + f[i-1][j-1];
		}
	}
}
int dp(int n){
	if(!n) return 0;//若n=0,直接返回0 
	vector<int> nums;
	while(n)   while(n){
        nums.push_back(n%B);
        n/=B;
    }
	int res = 0;
	int last = 0;//表示已经取了多少个1 
	for(int i = nums.size()-1; i>=0; i--){
		int x = nums[i];
		if(x){//大于1的方块和等于1的方块贡献值 
			res +=f[i][k-last];//加上第i位取0时的组合数, 
			if(x>1){//x大于1时,当此位取1时组合数 
				if(k - last - 1 >= 0) res += f[i][k-last-1];
				break;
			}
			else{//若x=1,则i位取1时,还要进行讨论, 后面i位不能随便取,也就不是组合数 
				last++;
				if(last>k) break;
			}
		}
		if(!i&&last==k) res++;//最右侧分支上的方案, 
	}
	return res;
}
int main(){
	init();
	int l,r;
	cin>>l>>r>>k>>B;
	cout<<dp(r)-dp(l-1)<<endl;
}