编辑距离

刷题记录2
给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

1. 插入一个字符
2. 删除一个字符
3. 替换一个字符

样例1：

输入: word1 = "horse", word2 = "ros"
输出: 3

原因:
(将 ‘h’ 替换为 ‘r’)horse -> rorse
(删除 ‘r’)rorse -> rose
(删除 ‘e’)rose -> ros

样例2：

输入: word1 = "intention", word2 = "execution"
输出: 5

原因:
(删除 ‘t’)intention -> inention
(将 ‘i’ 替换为 ‘e’)inention -> enention
(将 ‘n’ 替换为 ‘x’)enention -> exention
(将 ‘n’ 替换为 ‘c’)exention -> exection
(插入 ‘u’)exection -> execution

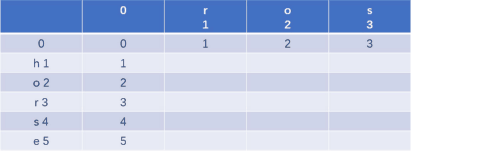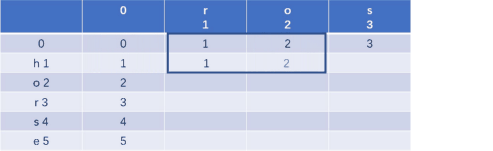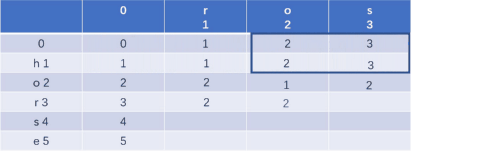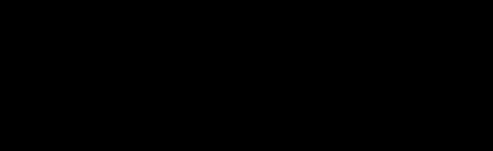
思路：利用动态规划，假设当前的最短编辑距离为dp[i][j]，i表示word1中第i个字母，j表示word2中第j个字母，可以得到如下的二维表。

为二维表赋边界值：

状态转移方程为：

判断当前字母相等：
	若相等：dp[i][j] = dp[i-1][j-1];
	若不相等：dp[i][j] = 1+min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]);

public class Main {
	public int minDistance(String word1, String word2) {
		if(word1.equals(""))return word2.length();
		if(word2.equals(""))return word1.length();
        int dp[][] = new int[word1.length()+1][word2.length()+1];
        for(int i = 0;i<dp.length;i++) {
        	dp[i][0] = i;
        }
        for(int i = 0;i<dp[0].length;i++) {
        	dp[0][i] = i;
        }
        for(int i = 1;i<dp.length;i++) {
        	for(int j = 1;j<dp[0].length;j++) {
        		if(word1.charAt(i-1)==word2.charAt(j-1))
        			dp[i][j] = dp[i-1][j-1];
        		else
        			dp[i][j] = 1+Math.min(dp[i-1][j], Math.min(dp[i][j-1], dp[i-1][j-1]));
        	}
        }
        for(int i = 0;i<dp.length;i++) {
        	for(int j = 0;j<dp[0].length;j++) {
        		System.out.print(dp[i][j]);
        	}
        	System.out.println();
        }
        return dp[dp.length-1][dp[0].length-1];
    }
}