卡特兰数

卡特兰数的递推式：

  h(0) = 1, h(1) = 1;

　h(n) = h(0)*h(n-1) + h(1)*h(n-2) + ... h(n-1)*h(0);

已知有n个元素，以及一个长度无限的栈，那么不同的出栈序列的个数就是h(n)，证明如下：

将n个元素按某种顺序排列，设x为最后一个出栈的元素，同时，x是这n个元素中的第k个，那么要让x最后一个出栈，只能先将k-1个元素进栈然后出栈，然后将k进栈，然后将剩余元素进栈出栈，最后k出栈，即出栈序列数为h(k-1)*h(n-k),又x可以为这n个元素中的任何一个，即k可以取1,2...n.

所以总的出栈序列数为h(0)*h(n-1) + h(1)*h(n-2)...h(n-1)*h(0)

同时只有一个元素或没有元素时出栈顺序只有一种，所以h(0) = 1,h(1) = 1,也可以使用当k = 1时，出栈序列就是h(n-1)来证明h(0) = 1.

 

所以要证明某一个序列数是卡特兰数，只要证明它满足卡特兰数的递归关系即可，比如给定n个节点可以生出几种形状不同的二叉树？

选个根节点，然后其左子树有k-1个，右子树有n-k个，很明显符合卡特兰数的递归关系

 

卡特兰数的一般项公式:

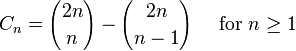
一般项可以以入栈出栈为原型，即有A，B两种操作，执行两种操作各n次，并且需要保证任意时刻执行A操作的次数不能比执行B操作的次数多。那么执行序列总数为卡特兰数的第n项。

一般项公式前半部分表示总执行序列数（包括合法的和非法的），后半部分的值为非法操作序列数。

比如：

有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？

就可以使用一般项公式得到

 

 

或者n对括号，可以选择连接，即()()或者递归(())，那么共有多少种不同的组合?

这个问题等价于n个左括号，n个右括号，那么合法的括号对序列有几个

 

或者2n个身高不同的人站成两排，要求每排都按照从低到高排列，同时任何第一排的人要比对应位置上第二排的人矮，

这个问题等价于将这2个人按照身高从矮到高排列，每个人选择去第一排还是第二排，但是必须保证第一排的人数不比第二排的少（第一排对应位置的人要比第二排的矮，即第一排的先到，即第一排要比第二排长）

 

再或者，对于一颗满二叉树，叶子节点一定比非叶子节点多一个，那么h(n)就表示有n个非叶子节点或者说有n+1个叶子节点的异构满二叉树的数量。

可以把叶子节点看成项，那么每一颗满二叉树就是给这些项加上不同的括号构成的语法树- -，那么问题就回到了括号问题上，

也可以递归的求，即因为是满二叉树，拿个根节点，左边1,2,3,....n个叶子节点，右边n,n-1,....1个叶子节点。

然后X(n) = X(1)*X(n-1) + ... X(n-1)*X(1)    n>=1 （至少有1个叶子节点，所以n从1开始）

所以X(n-1) = X(0)*X(n-2) + ... X(n-2)*X(0)   n>=0 （所有项下表减1，令n从0开始）

那么X(n) = X(0)*X(n-1) +  .. X(n-1)*X(0)

又X(0) = X(1) = 1

还是属于卡特兰数