AT_joisc2017_j 誘拐 2 (Abduction 2) 题解

对于一个矩形，已知其四边上不考虑其内部道路的所有答案，考虑其中车流指数最大的道路。

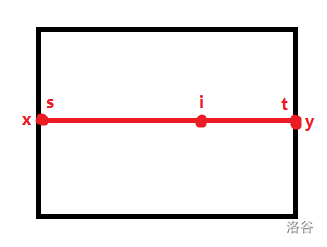
如图，红线为矩形中车流指数最大的道路，

两端点 $(k,s),(k,t)$ 不考虑矩形中内部道路的答案分别为 $x,y$，

则 $\forall i\in[s,t]$，可以确定 $(k,i)$ 的答案为 $\max\{x+i-s,y+t-i\}$。

若所询问的点在红线上，则可以返回答案，否则向所询问的点所在的子矩形递归。

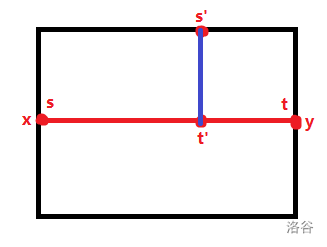
设所询问的点在上半个子矩形中。

如图，蓝线为子矩形中车流指数最大的道路，

端点 $(s',k')$ 在黑线上，已知不考虑子矩形中内部道路的答案，

端点 $(t',k')$ 在红线上，不考虑子矩形中内部道路的答案为 $\max\{x+t'-s,y+t-t'\}$。

若所询问的点在蓝线上，则可以返回答案，否则向所询问的点所在的子矩形递归。

特别地，最初整个矩形四边上不考虑其内部道路的所有答案为 $0$。

而且题目中有：

移动开始时，可以任意选择方向。

所以需要考虑开始时的移动方向，递归终止时如果不满足此时枚举的方向需要继续递归。

用 ST 表维护子矩形中车流指数最大的道路。

容易发现最坏情况下最多递归 $H+W$ 层，所以复杂度为 $O(Q(H+W))$。

#include <cstdio>
#include <algorithm>
using namespace std;
struct S
{
    int s, t;
    long long x, y;
    bool v;
} a[50050], b[50050];
int n, m, q, x, y;
long long s;
struct T
{
    int n;
    pair<int, int> a[20][50050];
    void B(int _)
    {
        n = _;
        for (int i = 1; i <= n; ++i)
            scanf("%d", &a[0][i].first), a[0][i].second = i;
        for (int i = 1; 1 << i <= n; ++i)
            for (int j = 1; j + (1 << i) - 1 <= n; ++j)
                a[i][j] = max(a[i - 1][j], a[i - 1][j + (1 << i - 1)]);
    }
    pair<int, int> Q(int x, int y)
    {
        if (x > y)
            return {0, 0};
        int k = __lg(y - x + 1);
        return max(a[k][x], a[k][y - (1 << k) + 1]);
    }
} X, Y;
long long D(int s1, int s2, int t1, int t2, int k1, int k2, int f, int g)
{
    auto P = X.Q(s1 + (f >> 0 & 1), t1 - (f >> 1 & 1)),
         Q = Y.Q(s2 + (f >> 2 & 1), t2 - (f >> 3 & 1));
    int x = P.second, y = Q.second;
    if (P > Q)
    {
        a[x] =
            {s2, t2,
             b[s2].v ? max(b[s2].x + x - b[s2].s, b[s2].y + b[s2].t - x) : 0,
             b[t2].v ? max(b[t2].x + x - b[t2].s, b[t2].y + b[t2].t - x) : 0,
             1};
        if (k1 == x)
        {
            if (g == 0)
                return D(s1, s2, x, t2, k1, k2, f | 2, g);
            if (g == 1)
                return D(x, s2, t1, t2, k1, k2, f | 1, g);
            if (g == 2)
                return a[x].x + k2 - s2;
            if (g == 3)
                return a[x].y + t2 - k2;
        }
        if (k1 > x)
            return D(x, s2, t1, t2, k1, k2, f | 1, g);
        if (k1 < x)
            return D(s1, s2, x, t2, k1, k2, f | 2, g);
    }
    if (P < Q)
    {
        b[y] =
            {s1, t1,
             a[s1].v ? max(a[s1].x + y - a[s1].s, a[s1].y + a[s1].t - y) : 0,
             a[t1].v ? max(a[t1].x + y - a[t1].s, a[t1].y + a[t1].t - y) : 0,
             1};
        if (k2 == y)
        {
            if (g == 0)
                return b[y].x + k1 - s1;
            if (g == 1)
                return b[y].y + t1 - k1;
            if (g == 2)
                return D(s1, s2, t1, y, k1, k2, f | 8, g);
            if (g == 3)
                return D(s1, y, t1, t2, k1, k2, f | 4, g);
        }
        if (k2 > y)
            return D(s1, y, t1, t2, k1, k2, f | 4, g);
        if (k2 < y)
            return D(s1, s2, t1, y, k1, k2, f | 8, g);
    }
}
void F(int x, int y, int g)
{
    for (int i = 1; i <= n; ++i)
        a[i].v = 0;
    for (int i = 1; i <= m; ++i)
        b[i].v = 0;
    s = max(s, D(1, 1, n, m, x, y, 0, g));
}
signed main()
{
    scanf("%d%d%d", &n, &m, &q);
    X.B(n);
    Y.B(m);
    while (q--)
    {
        scanf("%d%d", &x, &y);
        s = 0;
        if (x != 1)
            F(x, y, 0);
        if (x != n)
            F(x, y, 1);
        if (y != 1)
            F(x, y, 2);
        if (y != m)
            F(x, y, 3);
        printf("%lld\n", s);
    }
    return 0;
}