【学习笔记】可持久化线段树

目录

• 写在前面
• 关于可持久化
• 可持久化数组 & 可持久化线段树
  • 暴力做法
  • 一个小优化
  • 进一步优化
  • 练习
  • 主席树

写在前面

这是 CSP-S2 2020 考完后 5ab 写的第一篇文章，学的第一个新算法。

CSP-S2 考完后，5ab 就要朝着省选算法进发，学习省选内容喽。

关于可持久化

可持久化是一种思想，一种通过修改局部，拷贝局部数据的方法来达到多版本访问的目的。

这样说确实不太清楚。难道你就是这么学的？我们来看一个例子。

可持久化数组 & 可持久化线段树

给你一个序列，每一次基于一个历史版本单点修改某个数，或者询问某个数。

暴力做法

我们可以先考虑暴力：

1. 先将数组存下来；
2. 每一次操作，拷贝数组然后进行修改或者询问。

显而易见，这个操作的复杂度是 \(\mathcal{O}(nq)\)，不够优秀。我们得考虑一个更好的做法。

一个小优化

众所周知，遇事不决就分块，我们不妨将这个数组分块。

每一次操作，我们只要记录块内的修改即可。可以有 \(\mathcal{O}(q\sqrt{n})\) 的优秀复杂度，可以通过不小的数据。

进一步优化

我们考虑用线段树维护。这是一个很简单的推进——从分块到线段树。

注意到如果是线段树，每一次要拷贝的数据仅仅为一条链，如图：

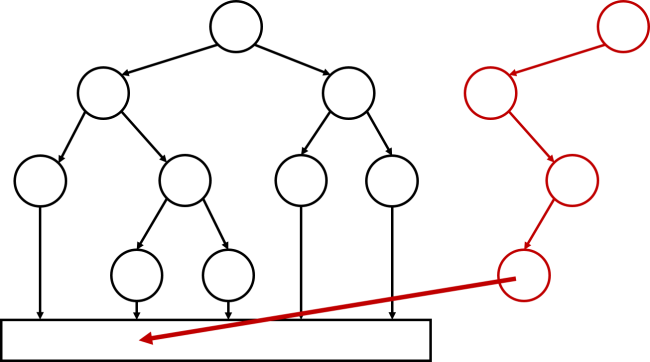
这个性质极其优美，但是，怎么样维持线段树的形态呢？

我们有一个极其暴力的做法：直接动态开点，然后将没有修改的部分直接指向原部分！

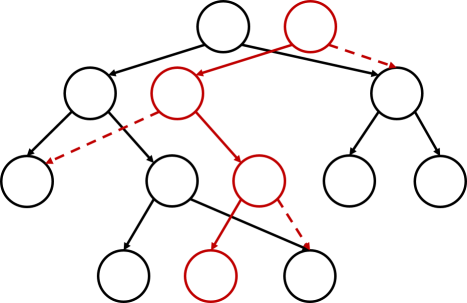
注意到这样的改进使单次修改的复杂度（无论是时间还是空间）都降到了 \(\mathcal{O}(\log n)\)。实际上，这就是可持久化数组。

当然，我们已经搭建了线段树结构，所以我们也实现了可持久化线段树。

练习

【模板】可持久化线段树 1（可持久化数组）

裸模板，直接用可持久化线段树即可。代码

主席树

get 到了可持久化线段树，我们就能够搞定许多以前做不出来的问题。如臭名昭著的区间第 \(k\) 大。

问题是，给定一个数列 \(a\)，每一次询问 \([l_i,r_i]\)，要求出该区间中的第 \(k\) 大。

形式地说，即若 \(\left<p_{l_i},p_{l_i+1},\cdots,p_{r_i}\right>=\left<l_i,l_i+1,\cdots,r_i\right>\) 且满足 \(a_{p_{l_i}}\le a_{p_{l_i+1}}\le\cdots\le a_{p_{r_i}}\)，给定 \(k\)，求 \(a_{p_{l_i+k-1}}\)。

当然，在数据比较小的时候可以使用排序法，但那实在是太慢了。我们考虑一种新思路。

注意到区间第 \(k\) 大就是有 \(k-1\) 比这个数小。那么我们只要可以快速询问有多少个数比自己小，那么不就能二分了吗？而询问恰恰好是线段树擅长的。

---

接下来我们引入一个概念，那就是权值线段树。

众所周知，线段树擅长处理区间问题。那么数的区间就是值域，所以权值线段树就是建立在值域上的线段树，当然得离散化。

接下来，我们建一棵权值线段树 \(T\) 在 \([L,R]\) 上，对于节点 \(i\) 所对应的区间为 \([l_i,r_i]\)。

考虑如下操作：

• 对于 \([L,R]\) 中的每一个数 \(x\)，在 \(T\) 的对应位置加上 \(1\)；
• 查询 \([l_i,r_i]\) 的区间和。

那么，操作 \(2\) 的结果就是 \([L,R]\) 的数在 \([l_i,r_i]\) 的数量。这样我们就可以愉快地二分了。

---

说了这么多，好像也并没有什么卵用，这和快排有什么区别呢？

注意到，每一次插入一个数，原序列就只有一个数被改动，那么我们就可以愉快地使用可持久化线段树来维护。

但是，这样我们也只能做到 \([1,r]\) 的区间第 \(k\) 大，距离真正的区间第 \(k\) 大还有一点距离。

但同时，我们又注意到这些线段树结构相同，而且每一次操作都是加法，那么我们就可以做前缀和！即，让 \(T_R\) 的每一个节点减去 \(T_{L-1}\) 的对应节点，那么得到的就是 \(T_{[L,R]}\)。

这就是主席树。（关于为什么要叫主席树，好像是因为发明者 HJT 与当年主席的相同）

\[\href{https://paste.ubuntu.com/p/CPWsPQD6Yh/}{\large\texttt{Code}} \]

不妨试一下模板题？