图论基础

蒟蒻的第一篇博客，多多支持啊~

\(P.S.\) 本文中部分图片来自§Chtholly§的图论入门

咳咳……进入正题

图的定义

图的结构

图由两个最基本的元素构成：

点和边

一条边一定连接两个点，这两个点被称为边的端点

许多点和的边组合在一起就构成了图

换句话说，所谓图，就是点和边的集合

（集合的性质：①元素不能重复，②内部元素没有顺序）

这就是所谓的\(G=(V,E)\),其中\(G(Graph)\)是图，\(V(Vertex)\)和\(E(Edge)\)分别是点和边的集合

图的具体化

用圆点表示点，用线段表示边

注意：画出来的图只作为示意使用，图的本质还是点和边的集合

图的用途

可以帮助我们高效的解决问题

图的分类

有向图和无向图

• 无向图

  无向图表示图中的边是不区分方向的，问题中的状态可以从一个边的任意一个节点转移到另一个节点

• 有向图

  有向图表示图中的边是不区分方向的，问题中的状态可以从一个边的一个节点转移到另一个节点，反之不行，有向图的方向通常用箭头表示

连通图和非连通图

（这个概念是针对无向图定义的）

• 连通图

  连通图就是指途中任意两个节点都可以通过边联通

• 非连通图

  非连通图就是指存在两个点，他们之间不能通过边联通

有权图和无权图

边也可以带权值

• 带权图

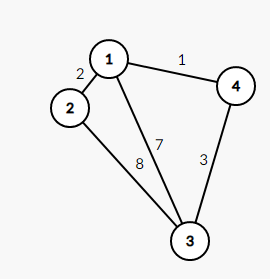
带权值的图叫带权图

• 无权图

  没有就叫无权图

图的其他定义

• 路径
  路径是指一系列边，其中相邻的两条边恰好有一个公共点

  （人话版：和生活中的路差不多从一个点走到另一个点经过的所有边的集合）

  其中有向图我们一般认为方向一样才算一条路径

• 简单路径

  简单路径则是指每个点最多经过一次的路径

• 子图

  原图的一个子集（还记得图的本质是点和边的集合吗），并且子集也是一个图

• 度数

  连接在这个点边数

  有向图还分入读和初度，顾名思义，就是这个点作为边的起点的次数和作为终点的次数

图的存储方式

邻接矩阵

临街矩阵的存图方式非常简单粗暴，也很简单

对于一个\(N\)个节点的图，邻接矩阵就是一个\(N*N\)的矩阵（二维数组），矩阵中每个元素都是\(0\)或\(1\)，为\(1\)则右边，为\(0\)则无边

特点

• 无向图的邻接矩阵沿对角线对称

• 如果图没有自环，矩阵对角线上的元素均为0

第二个特点一般没什么用，但是第一个要特别注意，在存无向图的时候要对两个方向都赋值为\(1\)

因为一条边可能只出现一次

如果出现重边，按照题意进行保留

注意：除非数据特别小，否则尽量少用，因为很容易爆

int n,m;//通常n表示点的个数，m表示变得个数 
int e[2100][2100];//e通常表示边，2100是点的个数（稍微大了一些，为了防止溢出） 
int main(){
	cin>>n>>m;
	int l,r; //l，r表示边的两个端点，为了方便输入 而使用 
	fot(int i=1;i<=m;i++)
	{
		cin>>l>>r;
		e[l][r]=1;//记得给两个位置赋值（如果是有向图就不需要） 
		e[r][l]=1;
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			cout<<<e[i][j];
		}
		cout<<endl;
	}
	return 0;
}

邻接链表

邻接链表就是用链表来存图

这里的邻接意思就是存储一条边连接的两个结点作为信息

邻接链表给每个结点分配一个链表，

链表的链结中存储着两类信息

• 一类是用于构成链表这个数据结构的信息，例如只想下一个链结或者上一个链结

• 另一类是关于变得信息，例如这条边的另一个端点是谁（一个端点已经确定，只需要存一个就够了）

定义

struct nds{
	int y,nxt;
}e[2100];
//e是链结，y是边的下一个端点，nxt是next，下一个链结的下标
int ltp=0,lk[110];
//ltp类似于栈的top，用来随时分配新的链结
//lk是link，lk[i]表示结点i的链表的第一个链结的下标 

插入

void ist(int x,int y){
	//ist是insert，在链表钱插入一个链结（或者说往图里插入一条边） 
	//x+y表示要建立一个从x指向y的结点，无向图需要再建立反向边 
	e[++ltp]={y,lk[x]};
	//让ltp+1，分配一个新节点，它的一个结点是y，下一个链结的lk[x] 
	//lk[x]也就是第一个链结，这要结合下一步理解 
	lk[x]=ltp;
	//让链表的第一个结点等于新分配的链结 
	e[++ltp]={x,lk[y]};
	lk[y]=ltp;
	//如果是无向图存图就要给相反的方向也插入一条边
	//需要注意的是，无向图存储用的边数是输入的边数*2（易错点） 
}

输入输出

int main()
{
	cin>>n>>m;
	int l,r;
	for(int i=1;i<=m;i++){
		cin>>l>>r;
		ist(l,r);
		//注意如果用read()快读的话，不能直接ist(read(),read());
		//参数的传递顺序是从右往左，在有向图里可能出错 
	}
	for(int k=1;k<=n;k++){
		cout<<k<<' ';
		//输出结点标号 
		for(int i=lk[k];i;i=e[i].net)
			//从k所在的第一个链结开始，沿着下一个链结遍历
			//知道遍历到头位置（下一个链结下标为0） 
			cout<<e[i].y<<' ';
			//输出另一个端点的标号 
		cout<<endl;
	}
} 

上面代码写的是无向图的存储方法

可以再函数中进行双向存储

也可以在函数中写单向的，在调用函数时双向调用

（两个结点调换位置调用两次）

图的遍历

图的遍历是指从一个（或多个）结点出发，沿着边遍历其他结点

dfs邻接矩阵

bool f[2100];
void dfs(int x){
	if(f[x]) return ;
	f[x]=true;//记忆化一下 
	for(int i=1;i<=n;i++)
		if(e[x][i])
			dfs(i); 
} 

bfs邻接链表

int q[2100],hd=0;//这是队列，hd是队尾 
bool f[2100];//记忆化一下 
void bfs(){
	q[hd=1]=1;//边赋值边初始化
	for(int k=1;k<=hd;k++)
	{
		//k相当于队头
		for(int i=lk[q[k]];i;i=e[i].nxt)
			//遍历和q[k]相连的所有边
			if(!f[e[i].y])
			{
				q[++hd]=e[i].y;
				f[e[i].y]=true;
			} 
	}
}