树、二叉树、查找算法总结

一. 思维导图

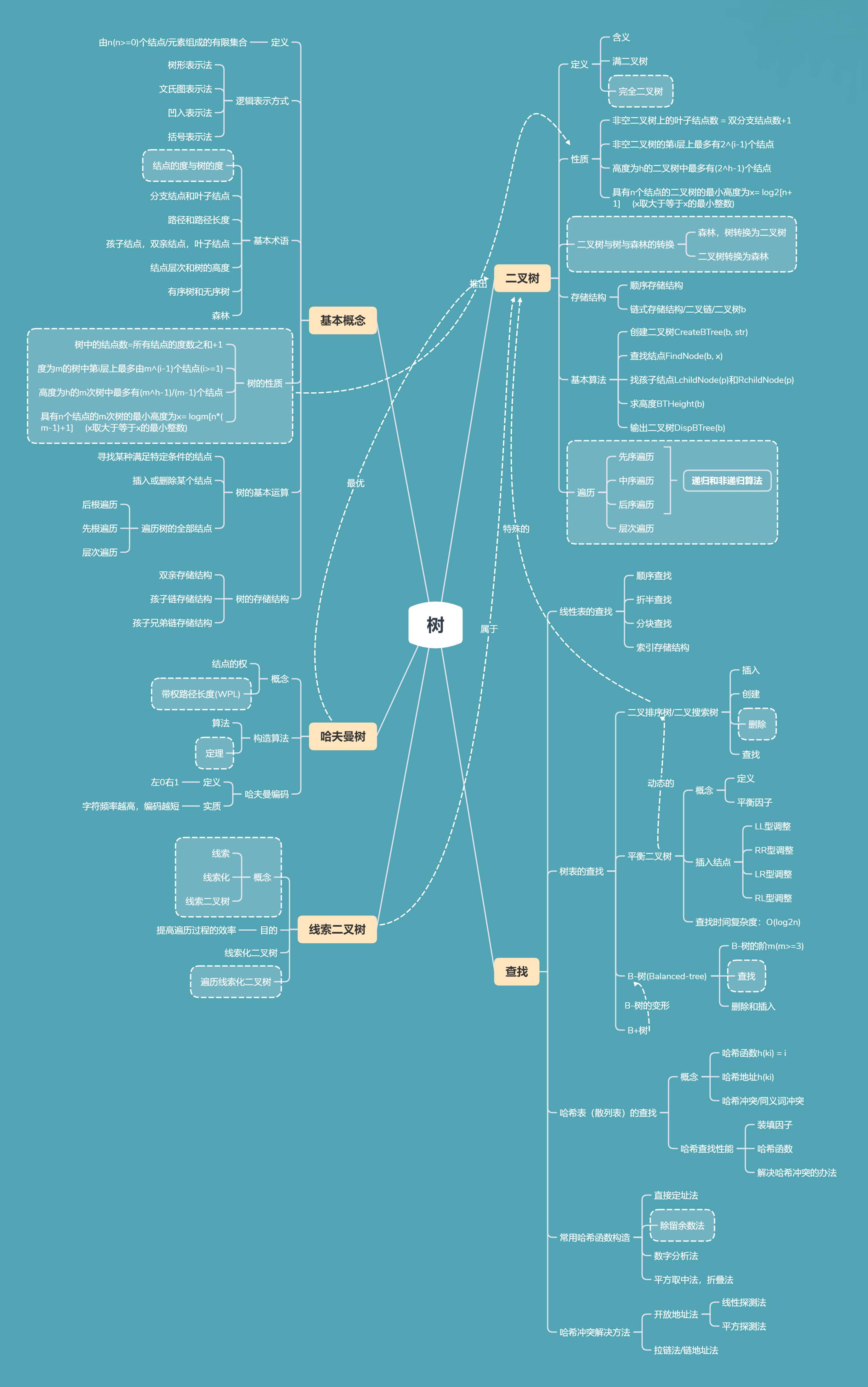
二. 概念笔记

- 结点的度：树中某个结点的子树的个数；
- 路径：若树中存在一个结点序列(ki1, ki2, ki3, ..., kj), 使得在这个结点序列中除了ki1以外任何一个结点都是前一个结点的后继结点 --> ki1-kj 这一序列为路径；
- 树的存储结构：
  1. 孩子链存储结构:
```
typedef struct node
{
	ElemType data;
	struct node* sons[MaxSons];    //指向孩子结点
}TSonNode;
```
  2. 双亲存储结构：
```
typedef struct
{
	ElemType data;
	int parent;
}PTree[MaxSize];
```
  3. 孩子兄弟链存储结构：
```
typedef struct tnode
{
	ElemType data;
	struct tnode* hp;   //指向兄弟
	struct tnode* vp;   //指向孩子结点
}TSBNode;
```
- 完全二叉树：二叉树中最多只有最下面两层的结点的度数可以小于2，并且最下面一层的叶子结点都依次排在最底层的最左边位置；
- 非空完全二叉树特点：
  1. 叶子结点只可能在最下面两层出现；
  2. 对于最大层次中的叶子结点，都依次排列在该层最左边位置上；
  3. 如果有度为1的结点，只可能有一个，且该节点只有左孩子，没有右孩子；
  4. 按层次编号的话，一旦出现编号为i的结点是叶子结点或只有左孩子，则编号大于i的结点均为叶子结点；
  5. 当结点总数n为奇数时，n1 = 0, 当结点总数n为偶数时，n1 = 1;
- 设二叉树上的叶子结点数为n0, 单分支结点数为n1, 双分支结点数为n2，总结点数为n, 则n = n0 + n1 + n2, 总分支数 = n - 1, n0 = n2 +1, 总分支数 = n1 + 2*n2;
- 树转换二叉树：
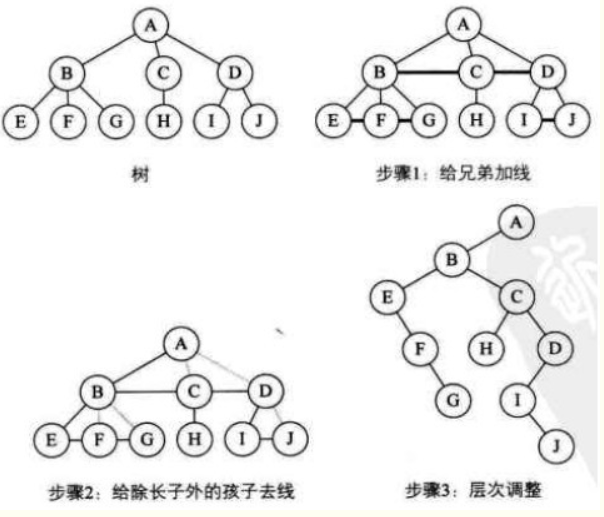
  1. 步骤：
    
    a. 加线。树中所有相邻兄弟之间加一条连线；
    
    b. 去线。树中每个结点只保留它和长子之间的连线，删除与其它孩子之间的连线；
    
    c. 调整。树的根结点为轴心，将整棵树进行顺时针转动45°，使其结构层次分明；
  2. 图示：
- 森林转换二叉树：
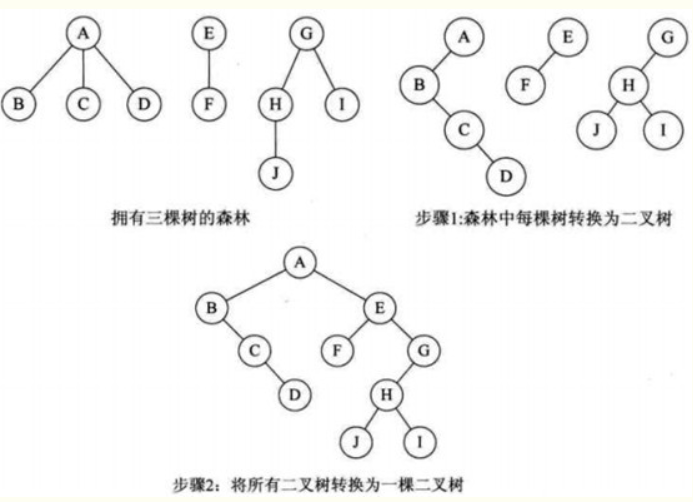
  1. 步骤：
    
    a. 将每棵树转换为二叉树；
    
    b.第一棵二叉树不动，第二棵二叉树开始，依次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子，最后用线连接起来；
  2. 图示：
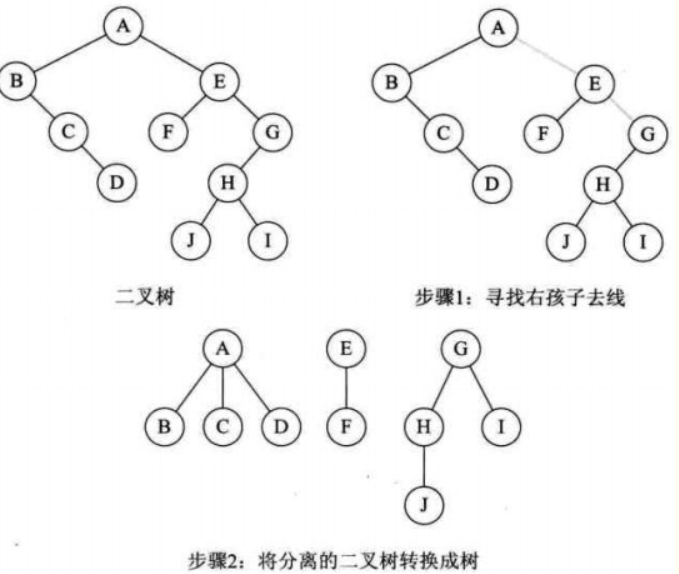
- 二叉树转换树：
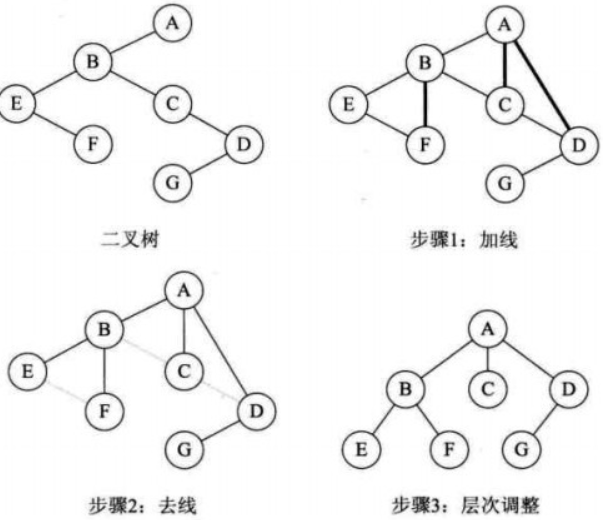
  1. 步骤(树转二叉树的逆过程)：
    
    a. 加线。若某结点是双亲的左孩子，则改结点的右孩子，右孩子的右孩子...都与它们的双亲连线；
    
    b. 减线。删除与右孩子的连线；
    
    c.调整；
    
    实质：”左子右兄“；
  2. 图示：
- 二叉树转换森林：
  1. 步骤(森林转换二叉树逆过程)：
    
    a. 删线。从根结点开始，若有右孩子就删线，直到删完；
    
    b. 二叉树转换树；
  2. 图示：

二叉顺序存储结构类型声明：
```
typedef ElemType SqBinTree[MaxSize];
```

二叉链/二叉树的链式存储结构类型声明：

typedef struct node
{
	ElemType data;
	struct node* lchild;
	struct node* rchild;
}BTNode;

二叉树递归遍历和非递归遍历（中序遍历为例）

递归：

void Inorder (BiTree T) 
{ 
	if (T) { 
		Inorder(T->lchild); // 遍历左子树 
		cout << T->data;    // 访问结点 
		Inorder(T->rchild); // 遍历右子树 
	} 
}

非递归：(栈)

void InOrderTraverse(BiTree T)
{ 
	InitStack(S); p = T; 
	声明q;                      //存放栈顶弹出元素 
	while (p || !StackEmpty(S))
	{ 
		if (p)
		{ 
			Push(S, p); 
			p = p->lchild; 
		}
		else
		{ 
			Pop(S, q); 
			cout << q->data; 
			p = q->rchild; 
		} 
	} 
}

- 线索二叉树：线索化的二叉树；
- 线索化:创建线索的过程；
- 线索：指向线性序列中的”前驱结点“和”后继结点“的指针；
- 线索二叉树作用：提高查找隔壁结点的效率；
- 折半查找：线性表是有序表，且必须为顺序表；
- 折半查找不适合链表存储结构，插入和删除时需要移动多个元素 --> 动态查找表；
- 二叉排序树声明结点类型：
```
typedef struct node
{
	ElemType key;
	InfoType data;
	struct node* lchild;
	struct node* rchild;
}BTNode;
```
- 删除二叉排序树关键字时，可以用k的前驱结点或后继结点补上；
- 平衡二叉树：
  1. 优点：使树的结构较好，从而提高查找运算的速度，缺点：使插入和删除运算变得复杂化，从而降低了他们的运算速度；
  2. 时间复杂度：一直是O(log2n);
  3. 适用范围：在内存里处理的少量数据；
- B-树：
  1. 适用范围：在硬盘存放的大量数据；
  2. 一颗B-树一共有n个关键字，则外部结点的个数为n+1;
- WPL：从根结点到改结点之间的路径长度和改结点的权的乘积之和；
- WPL 用来衡量算法的时间复杂度；
- 对于具有n0个叶子结点的哈夫曼树，共有2*n0 - 1个结点；
- 在一组字符的哈夫曼编码中，任意字符的哈夫曼编码不可能是另一字符哈夫曼编码的前缀；
哈希表：
- 什么情况适合使用：一组数据的关键字与存储关系存在某种映射关系时；
- 装填因子：已存入的元素n与哈希地址空间大小m的比值，控制在0.6~0.9的范围内；

三.疑难问题和解决方案

Q:哈希表查找失败时的查找平均次数;
A:即使要查找的元素的位置是空的也要算进去一个元素；

例：
1. 对于线性探测，因为它需要比较才知道是否为空，所以等概率情况下，
第一次：比较后为空，比较次数为1；

第二次：到第一个关键字为空的距离是2，比较次数为2；

第三次：比较后为空，比较次数为1；

第四次~第八次：到第一个关键字为空时都已经超过散列表长度，所以依次为6, 5, 4, 3, 2, 1;

不成功的元素一共有8个；
1. 对于链地址法，因为它在比较前要先判断是否为空，所以等概率条件下，
第一次：判断为空元素，比较次数为0；

第二次：一个关键字后为空，比较次数为1；

同理可得，第三次~第八次分别为0，1，2，1，1，0；

不成功的元素一共有8个；

posted @ 2020-04-26 20:53 黎里阅读(321) 评论(0) 编辑收藏举报

刷新页面返回顶部

黎里

树、二叉树、查找算法总结

一. 思维导图

二. 概念笔记

三.疑难问题和解决方案

公告