1.4 时间差分学习（Temporal Difference Learning）

时间差分学习（Temporal Difference Learning）

时间差分（Temporal Difference）

蒙特卡罗方法的主要缺点是：任务必须由有限的回合组成。这在实际中并不总是可行，而且值函数的更新必须等到整个回合结束后才能进行，从而导致学习速度变慢。

时间差分（Temporal Difference, TD） 方法的思想是：用一个由立即奖励和下一个状态的估计值组成的估计回报，来替代实际的完整回报：

\[ R_t \approx r(s, a, s') + \gamma \, V^\pi(s') \]

这来源于 @sec-dp 中提到的关系式：
\(R_t = r_{t+1} + \gamma R_{t+1}\)。

因此，状态值的更新规则为：

\[ V(s) \leftarrow V(s) + \alpha (r(s, a, s') + \gamma \, V(s') - V(s)) \]

其中的量：

\[ \delta = r(s, a, s') + \gamma \, V(s') - V(s) \]

称为奖励预测误差（Reward-Prediction Error, RPE）、TD 误差或一步优势（1-step advantage）。
它表示当前期望回报 \(V(s)\) 与采样目标（即时奖励 + 下一状态估计值）之间的“惊讶程度”。

• 若 \(\delta > 0\)：说明得到的奖励或下一状态好于预期，应提高该状态的估计值。
• 若 \(\delta < 0\)：说明结果差于预期，应降低该状态的估计值。
• 若 \(\delta = 0\)：完全符合预期，不应修改。

TD 方法的最大优势在于：值函数的更新可以在每次状态转移后立即进行，无需等待整个回合结束，甚至不需要定义“回合”。这种方式称为在线学习（online learning），可实现从单次转移的快速学习。
其主要缺点是：更新依赖于其他仍然错误的估计，因此初期的更新精度较低。

TD(0) 策略评估算法

while True:

• 从初始状态 \(s_0\) 开始。

• 对于回合中的每个时间步 \(t\)：

  • 按当前策略 \(\pi\) 选择动作 \(a_t\)。
  • 执行动作，观测到奖励 \(r_{t+1}\) 和下一个状态 \(s_{t+1}\)。
  • 计算 TD 误差：
  \[ \delta_t = r_{t+1} + \gamma V(s_{t+1}) - V(s_t) \]
  • 更新当前状态的值函数：
  \[ V(s_t) = V(s_t) + \alpha \, \delta_t \]
  • 若 \(s_{t+1}\) 为终止状态：break

TD 的偏差-方差权衡

相比蒙特卡罗使用真实回报，TD 使用回报的估计值：

• 增加偏差（bias）：因为估计在早期通常是错误的；
• 降低方差（variance）：仅即时奖励 \(r(s,a,s')\) 是随机的，而 \(V^\pi\) 是确定的。

因此，TD 通常得到次优解（suboptimal），但需要更少样本（更高采样效率）。

对于 Q 值，也有类似的 TD 更新公式：

\[ Q(s, a) \leftarrow Q(s, a) + \alpha (r(s, a, s') + \gamma Q(s', a') - Q(s, a)) \]

问题在于：更新时应使用哪一个下一步动作 \(a'\)？
是当前策略实际将采取的动作（即 \(\pi(s', a')\)），还是 Q 值最大的贪婪动作 \(a^* = \arg\max_a Q(s',a)\)？
这区分了同策略（on-policy）与异策略（off-policy）学习。

---

同策略 TD 学习：SARSA

SARSA（State–Action–Reward–State–Action） 使用下一步由策略 \(\pi(s', a')\) 采样得到的动作进行更新：

\[ Q(s, a) \leftarrow Q(s, a) + \alpha (r(s, a, s') + \gamma Q(s', \pi(s')) - Q(s, a)) \]

要求 \(\pi\) 是随机的（\(\epsilon\)-greedy 或 softmax）。

SARSA 算法

while True:

• 从初始状态 \(s_0\) 开始，使用策略 \(\pi\) 选择 \(a_0\)。

• 对于每一步：

  • 执行动作 \(a_t\)，观察到 \(r_{t+1}\)、\(s_{t+1}\)。
  • 使用当前策略 \(\pi\) 选择 \(a_{t+1}\)。
  • 更新 Q 值：
  \[ Q(s_t,a_t) = Q(s_t,a_t) + \alpha (r_{t+1} + \gamma Q(s_{t+1},a_{t+1}) - Q(s_t,a_t)) \]
  • 改进策略（\(\epsilon\)-greedy）：
  \[ \pi(s_t,a) = \begin{cases} 1-\epsilon, & a = \arg\max Q(s_t,a) \\ \frac{\epsilon}{|\mathcal{A}(s_t)|-1}, & \text{否则} \end{cases} \]
  • 若 \(s_{t+1}\) 为终止状态：break

---

异策略 TD 学习：Q-learning

Q-learning [@Watkins1989] 使用下一个状态的最大 Q 值更新当前状态：

\[ Q(s,a) \leftarrow Q(s,a) + \alpha (r(s,a,s') + \gamma \max_{a'} Q(s',a') - Q(s,a)) \]

Q-learning 算法

while True:

• 从初始状态 \(s_0\) 开始。

• 对于每个时间步：

  • 使用行为策略 \(b\)（如 \(\epsilon\)-greedy）选择 \(a_t\)；
  • 执行动作 \(a_t\)，观察 \(r_{t+1}\)、\(s_{t+1}\)；
  • 更新 Q 值：
  \[ Q(s_t,a_t) = Q(s_t,a_t) + \alpha (r_{t+1} + \gamma \max_a Q(s_{t+1},a) - Q(s_t,a_t)) \]
  • 贪婪更新策略：
  \[ \pi(s_t,a) = \begin{cases} 1, & a = \arg\max Q(s_t,a) \\ 0, & \text{否则} \end{cases} \]
  • 若 \(s_{t+1}\) 为终止状态：break

Q-learning 中，行为策略负责探索，而 SARSA 中探索由 \(\epsilon\)-soft 策略自身保证。
行为策略 \(b\) 通常采用 \(\epsilon\)-greedy 形式：以概率 \(1-\epsilon\) 选贪婪动作，概率 \(\epsilon\) 随机选其他动作。
在连续动作空间中，可添加噪声（如 Ornstein–Uhlenbeck 噪声）以促进探索。

虽然 Q-learning 是异策略算法，但不需要重要性采样，因为更新规则不依赖于行为策略 \(b\)：

\[Q^\pi(s,a) \leftarrow Q^\pi(s,a) + \alpha (r(s,a,s') + \gamma \max_{a'} Q^\pi(s',a') - Q^\pi(s,a)) \]

---

Actor-Critic 方法

在每次转移 \((s_t,a_t,r_{t+1},s_{t+1})\) 后，TD 误差：

\[ \delta_t = r_{t+1} + \gamma V(s_{t+1}) - V(s_t) \]

表示该动作的好坏。

• 若 \(\delta_t > 0\)：动作比预期好，应强化该动作并提高状态价值。
• 若 \(\delta_t < 0\)：动作比预期差，应削弱该动作并降低状态价值。

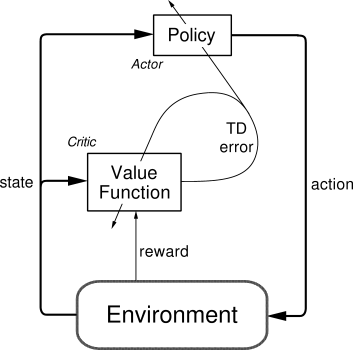
Actor-Critic 是一种 TD 方法，具有两个独立的存储结构：

• Actor（行为者）：表示并更新策略 \(\pi\)；
• Critic（评论者）：估计值函数 \(V(s)\) 并计算 TD 误差。

评论者计算：

\[ \delta_t = r_{t+1} + \gamma V(s_{t+1}) - V(s_t) \]

并用于更新：

\[ V(s_t) \leftarrow V(s_t) + \alpha \delta_t \]

Actor 根据该信号更新策略（如 Softmax 形式）：

\[\begin{cases} p(s_t,a_t) \leftarrow p(s_t,a_t) + \beta \delta_t \\ \pi(s,a) = \frac{\exp p(s,a)}{\sum_b \exp p(s,b)} \end{cases} \]

Actor-Critic 算法（基于偏好）

1. 初始化偏好 \(p(s,a)\) 和评论者 \(V(s)\)。

2. 对每个时间步 \(t\)：

   • 按策略 \(\pi\) 选择 \(a_t\)；
   • 执行动作，观测 \((r_{t+1}, s_{t+1})\)；
   • 计算 TD 误差：
   \[ \delta_t = r_{t+1} + \gamma V(s_{t+1}) - V(s_t) \]
   • 更新 Actor：
   \[ p(s_t,a_t) \leftarrow p(s_t,a_t) + \beta \delta_t \]
   • 更新 Critic：
   \[ V(s_t) \leftarrow V(s_t) + \alpha \delta_t \]

该结构的优点是：Actor 可采用任意形式（偏好、线性函数、神经网络等），并能高效地在大规模或连续动作空间中工作，学习随机策略。
但必须同策略学习：评论者必须评估当前 Actor 的动作，Actor 也必须依据当前 Critic 学习。

---

优势估计（Advantage Estimation）

n步优势（n-step Advantage）

MC 方法：高方差、低偏差。
TD 方法：低方差、高偏差。

为平衡两者，可使用 n步回报（n-step return）：

\[ R^n_t = \sum_{k=0}^{n-1} \gamma^k r_{t+k+1} + \gamma^n V(s_{t+n}) \]

其对应优势为：

\[ A^n_t = R^n_t - V(s_t) \]

当 \(n=1\) 时，\(A^1_t\) 即为 TD 误差。
合适的 \(n\) 可平衡偏差与方差：小 \(n\) 学得快但易次优，大 \(n\) 收敛好但需更多样本。

---

资格迹（Eligibility Traces）

TD 学习在稀疏奖励场景中收敛慢。
资格迹（eligibility trace）结合了 MC 的快速传播与 TD 的在线更新。

参数 \(\lambda \in [0,1]\) 控制 TD 误差的时间影响范围：

• 前向视图（Forward view）：

\[ R_t^\lambda = \sum_{k=0}^T (\gamma \lambda)^k \delta_{t+k} \]

需要未来信息，不支持在线更新。

• 后向视图（Backward view）：

\[ e(s,a) = \begin{cases} e(s,a)+1, & s=s_t,a=a_t\\ \lambda e(s,a), & \text{否则} \end{cases} \]

并更新所有 \((s,a)\)：

\[ Q(s,a) \leftarrow Q(s,a) + \alpha e(s,a)\delta_t \]

两种实现等价：前向依赖未来，后向计算量更大。
扩展形式：TD(\(\lambda\))、SARSA(\(\lambda\))、Q(\(\lambda\))。

TD(\(\lambda\)) 策略评估

对每步 \(t\)：

1. 按策略 \(\pi\) 选择动作，获得 \((r_{t+1}, s_{t+1})\)；
2. 计算 TD 误差：

\[\delta_t = r_{t+1} + \gamma V(s_{t+1}) - V(s_t) \]

3. 增加当前状态迹：

\[e_{t+1}(s_t) = e_t(s_t) + 1 \]

4. 对每个历史状态 \(s\)：

\[V(s) \leftarrow V(s) + \alpha \delta_t e_t(s) \]

并衰减：

\[e_{t+1}(s) = \lambda \gamma e_t(s) \]

---

广义优势估计（Generalized Advantage Estimation, GAE）

回顾 n 步优势：

\[A^n_t = \sum_{l=0}^{n-1} \gamma^l \delta_{t+l} \]

GAE 不固定 \(n\)，而是取加权平均：

\[A^{\text{GAE}(\gamma,\lambda)}_t = \sum_{l=0}^\infty (\gamma\lambda)^l \delta_{t+l} \]

• \(\lambda=0\) → TD 优势（高偏差、低方差）
• \(\lambda=1\) → MC 优势（低偏差、高方差）

调整 \(\lambda \in [0,1]\) 可平衡偏差与方差。
GAE 在实践中（如 PPO 算法）比 n 步优势表现更优。