动手学pytorch-线性回归

1.模型

\[\mathrm{Y} = \mathrm{WX} + b \]

2.数据集

• training set：已获得的，可用作模型训练的，带标签的数据集（对有监督模型来说）
• sample : 数据集中的一个样本
• label : 标签
• feature: 决定标签的特征

3.损失函数

\[l^{(i)}(\mathbf{w}, b) = \frac{1}{2} \left(\hat{y}^{(i)} - y^{(i)}\right)^2, \]

\[L(\mathbf{w}, b) =\frac{1}{n}\sum_{i=1}^n l^{(i)}(\mathbf{w}, b) =\frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)^2. \]

4.优化器

\[(\mathbf{w},b) \leftarrow (\mathbf{w},b) - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{(\mathbf{w},b)} l^{(i)}(\mathbf{w},b) \]

学习率: \(\eta\)代表在每次优化中，能够学习的步长的大小
批量大小: \(\mathcal{B}\)是小批量计算中的批量大小batch size
优化器总结博客：https://www.cnblogs.com/54hys/p/10224214.html

5.实例

5.1手写

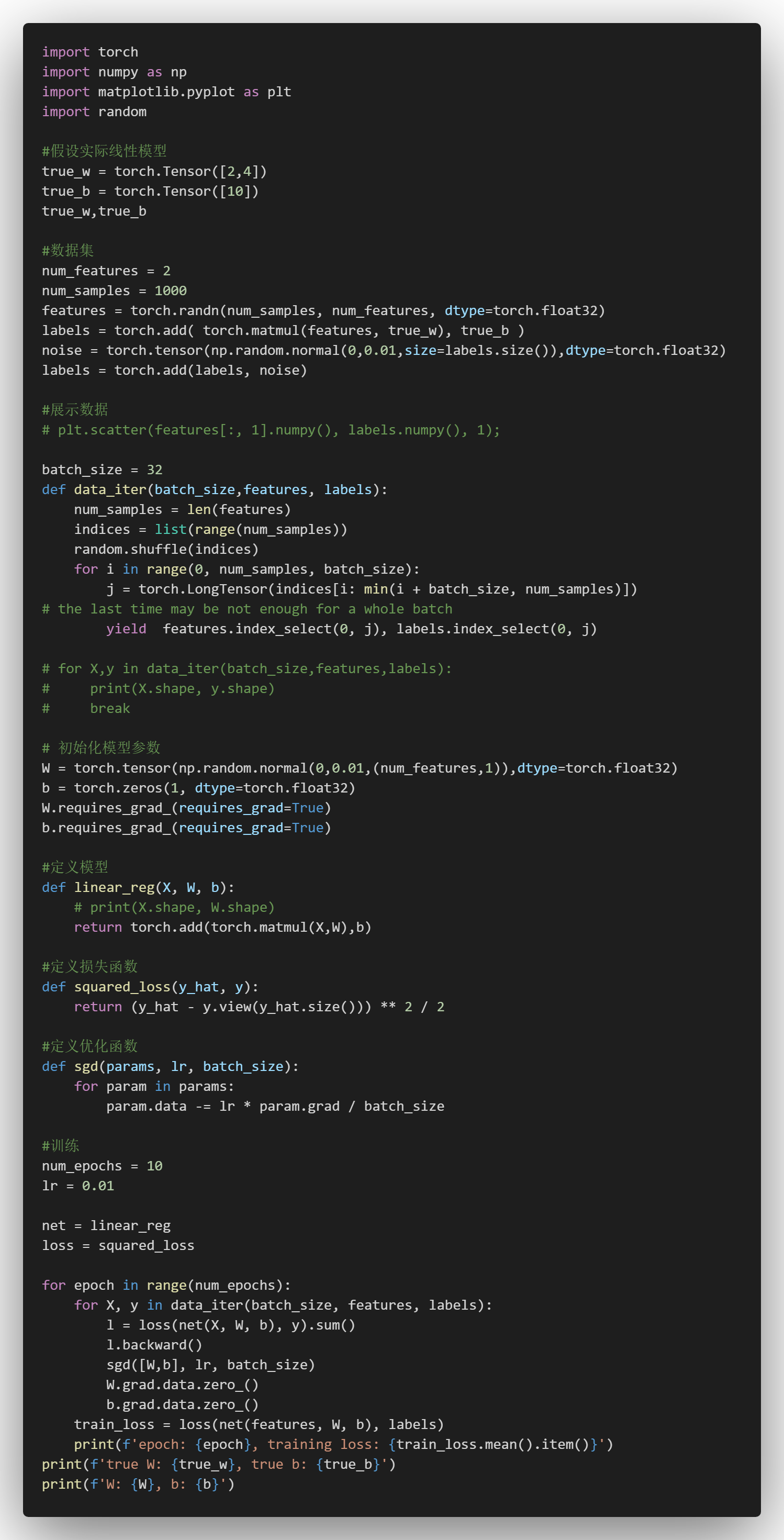
5.2使用pytorch简易实现