十大排序算法
可视化:https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
资料总结:https://www.bilibili.com/video/BV1DW4y1f7p8?spm_id_from=333.788.videopod.episodes&vd_source=69b667c94078fff1452cc5199e684fb7&p=51
比较排序
- 冒泡
- 插排
- 选择排序
- 希尔排序
- 快速排序
- 归并排序
- 堆排序
非比较排序
- 计数排序
- 桶排序
- 基数排序
1. 冒泡排序
算法过程:通过多次与相邻的元素比较与交换,使得最终的元素按升序排列。
可视化:
伪代码:
BubbleSort(arr):
n = length(arr)
for i = 0 to n-1:
for j = 0 to n-i-2:
if arr[j] > arr[j+1]:
swap(arr[j], arr[j+1])
Java代码:
public class BubbleSort{
public static void bubbleSort(int[] arr){
int n = arr,length;
for (int i = 0; i < n-1; i++){ //循环次数
for (int j = 0 ;j < n-i-2){ //比较的两个元素
if (arr[j] > arr[j+1]){
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
}
时间复杂度:(稳定)
- best:O(n)
- worst:O(n²)
- average:O(n²)
// 外层循环n次,内层循环n-i次,总的执行次数为O(n²)
2. 插入排序
算法过程:后一位元素向前做升序(倒序)排序,若比上一个元素大(小)则不断往前排序,直到遇到比自己小(大)的元素;从第二个元素开始循环到最后一位元素。
可视化:
伪代码:
InsertSort(arr):
n = length(arr);
for(i = 1; i < n-1; i ++): //循环次数为n次
key = arr[i]
j = i - 1
while(j >= 0 && arr[j] > key): //内层循环:arr[i]=arr[j+1],前后元素比较大小,若前大于后则交换,再继续往前比较
arr[j + 1] = arr[j]
j = j - 1
arr[j + 1] = key
Java代码:
public class InsertSort(){
public static void insertSort(int[] arr){
for(int i = 1; i < arr.length - 1; i ++){
int key = arr[i];
int j = i-1;
while(j > 0 && arr[j] > key){
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
}
时间复杂度:(稳定)
- best:O(n)
- worst:O(n²)
- average:O(n²)
// 外层循环n次,内层循环的执行次数与元素的插入位置有关,最差的情况为O(n)次,总的执行次数为O(n²)
3. 选择排序
算法过程:每次选择最小元素,将其放到已排序部分的末尾/开头 。
可视化:
伪代码:
SelectionSort(arr):
n = length(arr)
for i = 0 to n-1: //外层循环次数
min_index = i
for j = i+1 to n:
if arr[j] < arr[min_index]:
min_index = j
swap(arr[i], arr[min_index])
Java代码:
public class SelectionSort(){
public static void selectionSort(int[] arr){
int n = arr.length;
for (int i = 0; i < n; i++){
int min-index = 1;
for(int j = i + 1; j < n; j++){
if (arr[j] < arr[min-index]){
min_index = j;
}
int temp = arr[i];
arr[i] = arr[min_index];
arr[min_index] = temp;
}
}
}
}
时间复杂度:(稳定)
- O(n²)
// 选择排序中有两个嵌套循环,每次比较时都需要遍历整个未排序部分,总的执行次数为O(n²)
4.希尔排序
算法过程:将数组分割为若干个子数组,再分别对每个子数组进行插入排序,然后缩小子数组的间隔(例如第一次分割成数组里一定距离中每组只有两个的子数组,第二次为有四个元素的子数组...),最后对整体进行插入排序,直到整个数组有序。
可视化;
伪代码:
ShellSort(arr):
gap = length(arr) // 2
while gap > 0: //外循环:
for i = gap to length(arr)-1:
temp = arr[i]
j = i
while j >= gap and arr[j - gap] > temp: //如果当前元素arr[i]小于前面gap距离的元素arr[j-gap],则交换它们的位置。
arr[j] = arr[j - gap]
j = j - gap
arr[j] = temp
gap = gap // 2 //间隔继续减半,继续下一轮的排序
Java代码:
public class ShellSort{
public static void shellSort(int[] arr){
int n = arr.length;
int gap = >> n;
while(gap > 0){
for(int i = gap; i < n-1; i++){
temp = arr[i];
int j = i;
while(j >= gap && arr[j - gap] > temp){
arr[j] = arr[j - gap];
j = j - gap;
}
arr[j] = temp;
}
gap = >> gap;
}
}
}
时间复杂度:(不稳定)
- best:O(nlogn)
- worst:O(n²)
- average:O(n^1.5)
5.快速排序
5.1 分治法
- 先从数组中取出一个数作为基准数
- 分区过程中,把大于这个数的数放在基准数的右边,把小于这个数的数放在基准数的左边。
- 在对左右区间重复第二步,直到各个区间只有一个数。
5.2 单向扫描分区方法
算法过程:设计数组第一个元素为基准数,数组左侧有一个左指针由数组第二个元素向右移动,数组右侧有一个右指针由数组最后一个元素向左移动,当左指针指到比基准数小的则左指针继续往右移动,若左指针指到比基准数大的元素则与右指针的元素比较,若右指针此时指的元素比基准数大,则右指针往左移动,直到找到比基准数小的元素,并和此时的左指针所指的元素交换,左指针继续往右移动。直到右指针在左指针左侧,右指针指向最后一个小于基准数的元素,并与基准数交换;(单向扫描)
然后到下一次递归,递归的数组区间在数组最左侧和基准数,在基准数最左侧的元素排序完后依照上述方法排序基准数右侧元素。(此处对应QuickSort伪代码)
伪代码:
QuickSort(arr, low, high):
if low < high:
pi = LomutoPartition(arr, low, high) // 获取基准元素的正确位置
QuickSort(arr, low, pi - 1) // 对基准元素左侧的部分递归排序
QuickSort(arr, pi + 1, high) // 对基准元素右侧的部分递归排序
LomutoPartition(arr, low, high):
pivot = arr[low] // 选择基准元素为数组最左侧元素
big = high // big是右指针,指向比基准元大的数
sp = low + 1 //sp为左指针/扫描指针
while sp <= big:
if arr[sp] <= pivot:
sp ++
else:
swap arr[sp] and arr[big]
big --
swap arr[low] and arr[big] //交换右指针元素和基准数
return high //返回基准元的位置
Java代码:
public class QuickSortLomuto {
// Lomuto单向分区方法
public static int lomutoPartition(int[] arr, int low, int high) {
int pivot = arr[low];
int big = high;
int sp = low + 1;
while(sp <= big){
if(arr[sp] <= pivot){
sp ++;
}else{
int temp = arr[sp];
arr[sp] = arr[big];
arr[big] = temp;
big --;
}
}
int temp = arr[low];
arr[low] = arr[big];
arr[big] = temp;
return big;
}
public static vid quickSort(int[] arr, int low, int high){
if(low < high){
pi = LomutoPartition(arr, low, high) // 获取基准元素的正确位置
QuickSort(arr, low, pi - 1) // 对基准元素左侧的部分递归排序
QuickSort(arr, pi + 1, high) // 对基准元素右侧的部分递归排序
}
}
时间复杂度:
- best:O(nlogn)
- worst:O(n²)
- average:O(nlogn)
5.3 双向扫描分区方法
算法过程:设计数组的第一个元素为基准数,数组最左侧有一个左指针指向第二个元素,左指针指向的元素若小于等于基准数则继续向右移动,数组最右侧的右指针从最后一个元素开始向左移动,若指向大于基准数的元素则继续向左移动,若右指针指向的元素小于等于基准数,左指针指向的元素大于基准数,则左右两数交换;
当右指针在左指针左侧,则将基准数与右指针的元素交换。继续递归快速排序。
伪代码:
HoarePartition(arr, low, high):
pivot = arr[low] // 选择基准元素为数组最左侧元素
right = high // big是右指针,指向比基准元大的数
left = low + 1 //sp为左指针,指向比基准元小的数
while left <= right:
while arr[left] <= pivot && left<= right:
left ++
while arr[right] > pivot && left <= right:
right --
swap arr[left] and arr[right] //当左指针元素大于基准数和右指针元素小于等于基准数时,左右相交换
swap arr[low] and arr[right] //交换右指针元素和基准数
return right //返回基准元的位置
Java代码:
public class HoarePartition {
//HoarePartition双向分区方法
public static int HoarePartition(int[] arr, int low, int high) {
int pivot = arr[low];
int right = high;
int left = low + 1;
while(left <= right){
while(arr[left] <= pivot && left <= right){
left ++;
}
while(arr[right] > pivot && left <= right){
right --;
}
int temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
}
int temp = arr[right];
arr[right] = arr[low];
arr[low] = temp;
return big;
}
public static vid quickSort(int[] arr, int low, int high){
if(low < high){
pi = HoarePartition(arr, low, high) // 获取基准元素的正确位置
QuickSort(arr, low, pi - 1) // 对基准元素左侧的部分递归排序
QuickSort(arr, pi + 1, high) // 对基准元素右侧的部分递归排序
}
}
时间复杂度:
- best:O(nlogn)
- worst:O(n²)
- average:O(nlogn)
5.4 有相同元素的快速排序
算法过程:有三个指针,一个指向比基准数小的元素(s),一个指向比基准数大的元素(b),一个指向与基准数相等的元素(e);s指针和e指针同时从第一个元素出发向右移动,当s,e指向的元素小于等于基准数的则继续向右移动,当等于时e指针指向等于的元素,若继续移动s直到遇到小于基准数的元素则s与e交换,并且s与e继续往左移动;当s指向的元素大于基准数时,s与b交换,b继续往右移动。
当s在b的右侧时停止排序,并且将基准数与arr[e-1]交换。
6.归并排序
算法过程:把数组递归分成两组,然后在各个两组内进行排序
伪代码:
MergeSort(arr):
if length(arr) <= 1:
return arr
mid = length(arr) // 2
left = MergeSort(arr[0..mid-1])
right = MergeSort(arr[mid..end])
return Merge(left, right)
Merge(left, right):
result = []
while left and right:
if left[0] < right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
result += left + right
//在上述 while 循环结束后,left 和 right 中至少有一个数组为空。此时,另一个数组中可能还有元素(这些元素已经是有序的),将剩下的元素直接添加到 result 中。
return result
Java代码:
public class MergeSort {
public static int[] mergeSort(int[] arr) {
if (arr.length <= 1) {
return arr;
}
int mid = arr.length / 2;
int[] left = mergeSort(Arrays.copyOfRange(arr, 0, mid));
int[] right = mergeSort(Arrays.copyOfRange(arr, mid, arr.length));
return merge(left, right);
}
private static int[] merge(int[] left, int[] right) {
int[] result = new int[left.length + right.length];
int i = 0, j = 0, k = 0;
while (i < left.length && j < right.length) {
if (left[i] < right[j]) {
result[k++] = left[i++];
} else {
result[k++] = right[j++];
}
}
while (i < left.length) {
result[k++] = left[i++];
}
while (j < right.length) {
result[k++] = right[j++];
}
return result;
}
}
时间复杂度:O(nlogn)
7.堆排序
算法过程:从子树开始,若是小顶堆则将对比母节点和左右节点,若有小于的母节点的子节点则相互交换,然后递归到最终的根节点;大顶堆则相反。
伪代码:
【小顶堆-逆序】
MinHeap(arr):
for x from n/2 - 1 to 0:
n = arr.length
MinHeapFixDown(arr,i,n);
MinHeapFixDown(arr,i,n):
left = 2*i + 1 //左孩子节点位置
right = 2*i + 2 //右孩子节点位置
if left >= n :
return //判断左孩子越界
min = left
if right >= n:
return //判断右孩子越界
min = left
else:
if arr[left]<arr[right]:
min = right
//判断左右节点哪个更小
if arr[i] < arr[min]:
return //如果arr[i]比两个孩子节点都小则不用调整
swap(arr[i],arr[min])
//否则找到最小的子节点并交换
MinHeapFixDown(arr,min,n) //继续递归调整
Java代码:
【小顶堆-逆序】
public class HeapSort{
public static void heapSort(int[] arr){
for (int i = n/2 - 1; i >= 0;i --){
int n = arr.length;
MinHeapFixDown(arr,i,n);
}
}
public static void MinHeapFixDown(int[] arr,int i,int n){
int left = 2*i + 1; //左孩子节点位置
int right = 2*i + 2; //右孩子节点位置
if(left >= n){
return; //判断左孩子越界
}
int min = left;
if (right >= n){
return; //判断右孩子越界
min = left;
}
else{
if arr[left] < arr[right]{
min = right;
}
}
//判断左右节点哪个更小
if (arr[i] < arr[min]){
return; //如果arr[i]比两个孩子节点都小则不用调整
}
int temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
//否则找到最小的子节点并交换
MinHeapFixDown(arr,min,n); //继续递归调整
}
}
时间复杂度:O(nlogn)
8.计数排序
算法过程:用一个辅助数组对数组中出现的元素进行计数,若出现n则在辅助数组的第n-1位会+1;
//优点:速度快
//缺点:数据范围大且系数,辅助空间大且系数,会造成空间的浪费
伪代码:
CountingSort(arr):
k = max(arr) // 找到数组中的最大值 k
count = array of size (k + 1) // 创建一个计数数组,记录每个元素的出现次数
result = empty array of same size as arr // 创建一个输出数组
// 初始化计数数组
for i from 0 to k:
count[i] = 0 // 初始化每个元素出现的次数为 0
// 统计每个元素出现的次数
for i from 0 to length(arr) - 1:
count[arr[i]] = count[arr[i]] + 1 // 对应元素的计数增加 1
// 修改计数数组,使每个元素的值等于小于等于它的元素的总个数
for i from 1 to k:
count[i] = count[i] + count[i - 1] // 将每个位置的值更新为该元素及前面元素的总数
// 构造排序后的结果
for i from length(arr) - 1 down to 0:
result[count[arr[i]] - 1] = arr[i] // 将元素放到输出数组中
count[arr[i]] = count[arr[i]] - 1 // 更新计数数组中的次数
return result // 返回排序后的数组
Java代码:
import java.util.Arrays;
public class CountingSort {
public static int[] countingSort(int[] arr) {
// 如果数组为空或长度为1,直接返回原数组
if (arr == null || arr.length <= 1) {
return arr;
}
// 找到最大值和最小值
int max = Arrays.stream(arr).max().getAsInt();
int min = Arrays.stream(arr).min().getAsInt();
// 计算计数数组的大小
int range = max - min + 1;
// 创建计数数组
int[] count = new int[range];
int[] result = new int[arr.length];
// 统计每个元素的出现次数
for (int i = 0; i < arr.length; i++) {
count[arr[i] - min]++; // 将元素值作为索引,增加计数
}
// 修改计数数组,累加每个位置的值
for (int i = 1; i < range; i++) {
count[i] += count[i - 1]; // 累加
}
// 构造排序后的数组
for (int i = arr.length - 1; i >= 0; i--) {
result[count[arr[i] - min] - 1] = arr[i]; // 根据计数将元素放到结果数组
count[arr[i] - min]--; // 更新计数
}
return result; // 返回排序后的数组
}
public static void main(String[] args) {
int[] arr = {4, 2, 2, 8, 3, 3, 1};
System.out.println("Original Array: " + Arrays.toString(arr));
int[] sortedArr = countingSort(arr);
System.out.println("Sorted Array: " + Arrays.toString(sortedArr));
}
}
时间复杂度::O(n+k)
9.桶排序
算法过程:先创建桶,将元素(value/(max=1)n)分配到各自的桶内后进行桶内的排序*,然后在将所有的桶内的元素按顺序合并在一起。
伪代码:
BucketSort(arr):
n = length(arr)
if n <= 1:
return arr
# Step 1: 找到数据的最小值和最大值
min_value = min(arr)
max_value = max(arr)
# Step 2: 创建桶
num_buckets = n
bucket_range = (max_value - min_value) / num_buckets
buckets = new List[num_buckets]
# Step 3: 将元素分配到桶中
for i = 0 to n-1:
bucket_index = (arr[i] - min_value) / bucket_range
buckets[bucket_index].add(arr[i])
# Step 4: 对每个桶内的元素进行排序
for i = 0 to num_buckets-1:
sort(buckets[i]) # 可以使用插入排序或其他排序
# Step 5: 合并桶内元素
result = []
for each bucket in buckets:
result.addAll(bucket)
return result
Java代码;
import java.util.*;
public class BucketSort {
public static void bucketSort(float[] arr) {
int n = arr.length;
if (n <= 1) {
return;
}
// Step 1: 找到数据的最小值和最大值
float minValue = arr[0];
float maxValue = arr[0];
for (int i = 1; i < n; i++) {
if (arr[i] < minValue) minValue = arr[i];
if (arr[i] > maxValue) maxValue = arr[i];
}
// Step 2: 创建桶
int numBuckets = n;
List<Float>[] buckets = new List[numBuckets];
for (int i = 0; i < numBuckets; i++) {
buckets[i] = new ArrayList<>();
}
// Step 3: 将元素分配到桶中
float range = (maxValue - minValue) / numBuckets;
for (int i = 0; i < n; i++) {
int index = (int) ((arr[i] - minValue) / range);
if (index == numBuckets) {
index--;
}
buckets[index].add(arr[i]);
}
// Step 4: 对每个桶内的元素进行排序
for (int i = 0; i < numBuckets; i++) {
Collections.sort(buckets[i]);
}
// Step 5: 合并桶内元素
int index = 0;
for (int i = 0; i < numBuckets; i++) {
for (float num : buckets[i]) {
arr[index++] = num;
}
}
}
// 测试
public static void main(String[] args) {
float[] arr = {0.42f, 0.32f, 0.23f, 0.11f, 0.56f, 0.78f};
bucketSort(arr);
System.out.println(Arrays.toString(arr));
}
}
时间复杂度:
- best:O(nlogn)
- worst:O(n²)
10.基数排序
算法过程:通过按位对数字进行排序,逐步从最低位到最高位进行排序。其排序过程是分步进行的,每步依赖于数字的某一位(从最低位开始),使用稳定的排序算法(如计数排序)对当前位进行排序。
伪代码:
RadixSort(arr):
max = findMax(arr) // 找到数组中的最大值
exp = 1 // exp表示当前位,初始为1(即最低位)
while max / exp > 0: // 当最高位的数字还未被处理时,循环
countingSortByDigit(arr, exp)
exp *= 10 // 处理下一个位
countingSortByDigit(arr, exp):
n = length(arr)
output = new array of size n
count = new array of size 10 (for digits 0 to 9)
// 计算每个数字在当前位的出现次数
for i = 0 to n-1:
index = (arr[i] / exp) % 10
count[index] += 1
// 修改count数组,count[i]保存的是小于等于i的元素数量
for i = 1 to 9:
count[i] += count[i-1]
// 构建输出数组
for i = n-1 down to 0:
index = (arr[i] / exp) % 10
output[count[index] - 1] = arr[i]
count[index] -= 1
// 将输出数组复制到原数组
for i = 0 to n-1:
arr[i] = output[i]
Java代码:
import java.util.Arrays;
public class RadixSort {
public static void radixSort(int[] arr) {
// 找到最大值
int max = findMax(arr);
// 从最低位开始排序
for (int exp = 1; max / exp > 0; exp *= 10) {
countingSortByDigit(arr, exp);
}
}
// 找到数组中的最大值
private static int findMax(int[] arr) {
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
return max;
}
// 根据当前位exp进行计数排序
private static void countingSortByDigit(int[] arr, int exp) {
int n = arr.length;
int[] output = new int[n];
int[] count = new int[10]; // 计数数组,存储每个数字出现的频率
// 计算当前位的数字的频率
for (int i = 0; i < n; i++) {
int index = (arr[i] / exp) % 10;
count[index]++;
}
// 修改计数数组,count[i]表示小于等于i的数字个数
for (int i = 1; i < 10; i++) {
count[i] += count[i - 1];
}
// 从后往前遍历原数组,确保排序的稳定性
for (int i = n - 1; i >= 0; i--) {
int index = (arr[i] / exp) % 10;
output[count[index] - 1] = arr[i];
count[index]--;
}
// 将排序后的数组复制回原数组
System.arraycopy(output, 0, arr, 0, n);
}
// 测试基数排序
public static void main(String[] args) {
int[] arr = {170, 45, 75, 90, 802, 24, 2, 66};
System.out.println("Original Array: " + Arrays.toString(arr));
radixSort(arr);
System.out.println("Sorted Array: " + Arrays.toString(arr));
}
}
时间复杂度:O(d * (n + k))
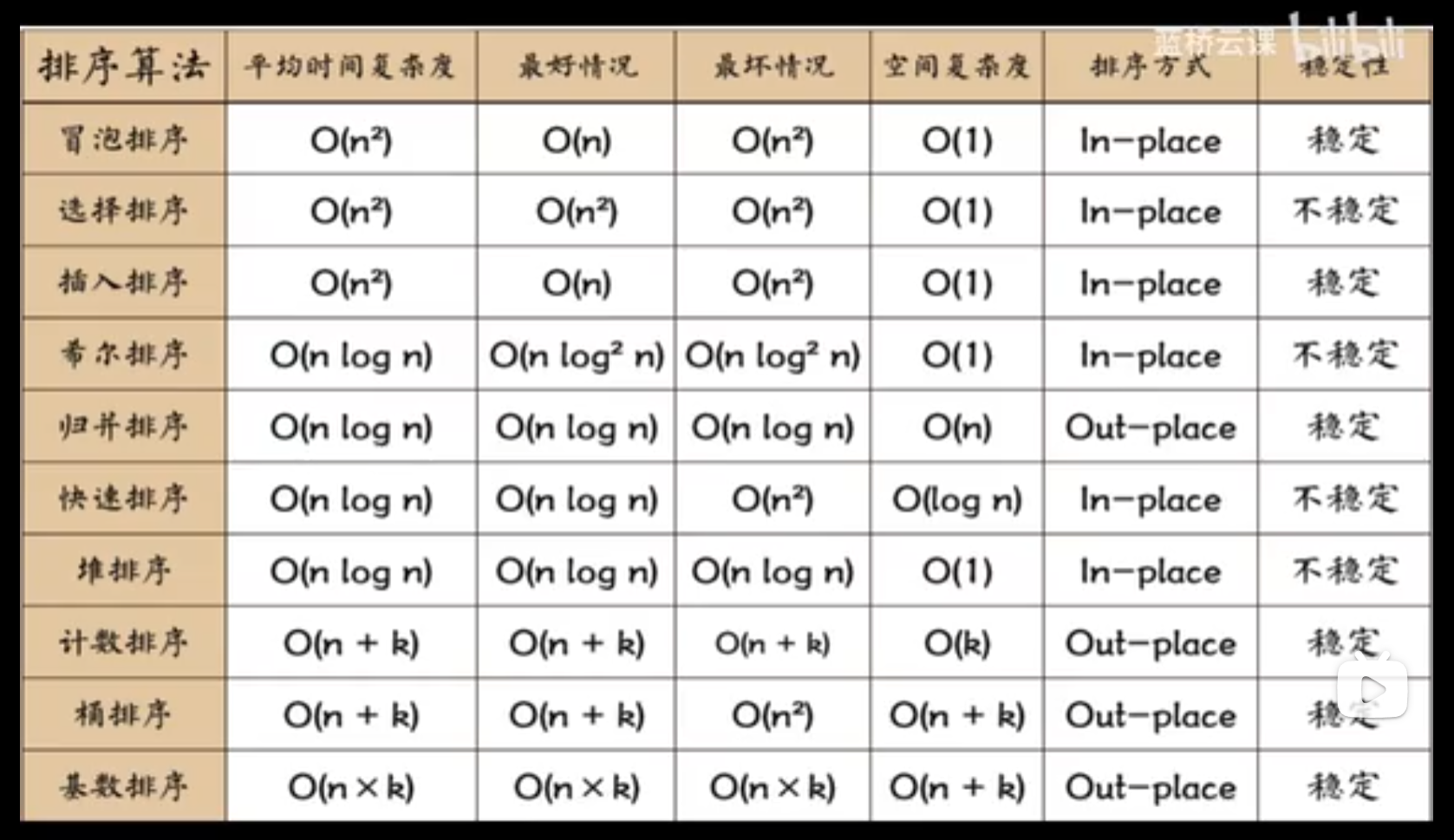
十种排序算法的时间复杂度总结



 浙公网安备 33010602011771号
浙公网安备 33010602011771号