2. Pytorch基础

2.1 张量

2.2.1 简介

　　几何代数中定义的张量是基于向量和矩阵的推广。比如我们可以将标量视为零阶张量，矢量可以视为一阶张量，矩阵就是二阶张量。

 

张量维度	代表含义
0维	标量（数字）
1维	向量
2维	矩阵
3维	时序数据、文本数据、单张彩色图片（RGB)
4维	图像
5维	视频

　　张量的核心是数据容易，包含数字等数据，可想象成是数字的水桶。

　　例子：一个图像可以用三个字段表示：

（width, height, channel) = 3D

　　处理一组图片：

（batch_size, width, height, channel) = 4D

　　在Pytorch中，torch.Tensor是存储和变换数据的主要工具。

2.1.2 创建Tensor

　　1. 随机初始化矩阵：通过torch.rand()构造一个随机初始化矩阵：

import torch
x = torch.rand(4,3)
print(x)

输出：

tensor([[0.7569, 0.4281, 0.4722],
        [0.9513, 0.5168, 0.1659],
        [0.4493, 0.2846, 0.4363],
        [0.5043, 0.9637, 0.1469]])

　　2.全0矩阵的构建：通过torch.zeros()构造全0矩阵，并且通过dtype参数设置数据类型为long。还可通过torch.zero_()和torch.zero_like()将现有矩阵转换成全0矩阵。

import torch
x = torch.zeros(4, 3, dtype = torch.long)
print(x)

输出：

tensor([[0, 0, 0],
        [0, 0, 0],
        [0, 0, 0],
        [0, 0, 0]])

　　3. 张量的构建：通过torcch.tensor()直接使用数据，构造一个张量：

import torch
x = torch.tensor([5, 3])
print(x)

输出：

tensor([5.0000, 3.0000])

　　4. 基于已经存在的tensor，创建一个tensor：

# 创建一个新的全1矩阵tensor，返回的tensor默认具有相同的torch.dtype和torch.device
# 或 使用x = torch.ones(4, 3, dtype = torch.double)
x = x.new_ones(4, 3, dtype = torch.double)
print(x)

输出：

tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]], dtype=torch.float64)

　　

# 重置数据类型
x = torch.randn_like(x, dtype = torch.float64)
print(x)
# 结果会有一样的size
print(x.size)
# 获取它的维度信息
print(x.shape)

tensor([[ 2.7311, -0.0720,  0.2497],
        [-2.3141,  0.0666, -0.5934],
        [ 1.5253,  1.0336,  1.3859],
        [ 1.3806, -0.6965, -1.2255]])
torch.Size([4, 3])
torch.Size([4, 3])

　　返回的torch.Size其实是一个tuple，⽀持所有tuple的操作。我们可以使用索引操作取得张量的长、宽等数据维度。

　　5. 常见的构造Tensor的方法：

　　

函数	功能
Tensor(sizes)	基础构造函数
tensor(data)	类似于np.array(data)
ones(sizes)	全1
zeros(sizes)	全0
eye(sizes)	对角为1，其余为0
arange(s, e, step)	从s到e，步长为step，左闭右开
linsapce(s, e, step)	从s到e，均分成step份
rand/randn(size)	rand[0,1)是均匀分布； randn是服从N(0, 1)的正态分布
normal(mean, std)	正态分布（均值，标准差）
randperm(m)	随机排列

2.1.3 张量的操作

　　1. 加法操作

import torch
y = torch.rand(4,3)
print(x+y)
print(torch.add(x,y))

## in-place 原值修改
y.add_(x)
print(y)

依次输出：

tensor([[ 2.8977,  0.6581,  0.5856],
        [-1.3604,  0.1656, -0.0823],
        [ 2.1387,  1.7959,  1.5275],
        [ 2.2427, -0.3100, -0.4826]])
tensor([[ 2.8977,  0.6581,  0.5856],
        [-1.3604,  0.1656, -0.0823],
        [ 2.1387,  1.7959,  1.5275],
        [ 2.2427, -0.3100, -0.4826]])
tensor([[ 2.8977,  0.6581,  0.5856],
        [-1.3604,  0.1656, -0.0823],
        [ 2.1387,  1.7959,  1.5275],
        [ 2.2427, -0.3100, -0.4826]])

　　2.索引操作

　　注：索引出来的结果与原数据共享内存，修改一个，另一个会随着修改。若不想修改，可采用copy()等方法。

import torch
x = torch.rand(4,3)
# 取第二列
print(x[:, 1]) 

输出：

tensor([-0.0720,  0.0666,  1.0336, -0.6965])

y = x[0,:]
y += 1
print(y)
print(x[0, :]) # 源tensor也被改了了

输出：

tensor([3.7311, 0.9280, 1.2497])
tensor([3.7311, 0.9280, 1.2497])

　　3. 维度变换：张量的维度变换方法有torch.view()和torch.reshape()

x = torch.randn(4, 4)
y = x.view(16)
z = x.view(-1,8) # -1是指该维由其它维度决定
print(x.size(), y.size(), z.size())

输出：

torch.Size([4, 4]) torch.Size([16]) torch.Size([2, 8])

　　注：torch.view()返回的新tensor与源tensor共享内存（二者是同一个tensor），更改其中一个，另一个会随着改变。（view只改变了对这个张量的观察角度）

x += 1
print(x)
print(y) # 也加了了1

输出：

tensor([[ 1.3019,  0.3762,  1.2397,  1.3998],
        [ 0.6891,  1.3651,  1.1891, -0.6744],
        [ 0.3490,  1.8377,  1.6456,  0.8403],
        [-0.8259,  2.5454,  1.2474,  0.7884]])
tensor([ 1.3019,  0.3762,  1.2397,  1.3998,  0.6891,  1.3651,  1.1891, -0.6744,
         0.3490,  1.8377,  1.6456,  0.8403, -0.8259,  2.5454,  1.2474,  0.7884])

　　torch.view()会改变原始张量，若希望原始张量和变换后的张量互相不影响（不共享内存），需使用torch.reshape()。

　　但是torch.reshape()并不能保证返回的是其拷贝值，所以不推荐使用。

　　推荐方法：先用clone()创建一个张量副本，再使用torch.view()进行维度变换。

　　注：使用clone()会被记录在计算图中，即梯度回到副本时也会传到源Tensor。

　　4. 取值操作：可通过使用。item()来获取tensor元素的values，而不获得其他性质。

import torch
x = torch.randn(1) 
print(type(x)) 
print(type(x.item()))

输出：

<class 'torch.Tensor'>
<class 'float'>

　　PyTorch中的 Tensor 支持超过一百种操作，包括转置、索引、切片、数学运算、线性代数、随机数等等，具体使用方法可参考官方文档

2.1.4 广播操作

　　当对两个形状不同的tensor进行按元素运算时，可能会触发广播(broadcasting)机制：先适当的复制元素使这两个tensor形状相同后再按元素运算。

x = torch.arange(1, 3).view(1, 2)
print(x)
y = torch.arange(1, 4).view(3, 1)
print(y)
print(x + y)

输出：

tensor([[1, 2]])
tensor([[1],
        [2],
        [3]])
tensor([[2, 3],
        [3, 4],
        [4, 5]])

　　x为1行2列，y为3行1列，若要计算x+y，则将x的1行广播为3行（第1行的元素复制到2，3行），y的1列广播为2列（第1列的元素复制到第2列）。

 2.2 自动求导

　　PyTorch 中，所有神经网络的核心是 autograd包。autograd包为张量上的所有操作提供了自动求导机制。

　　它是一个在运行时定义 ( define-by-run ）的框架，这意味着反向传播是根据代码如何运行来决定的，并且每次迭代可以是不同的。

 　　2.2.1 Autograd简介

　　torch.Tensor是这个包的核心类。若设置它的属性 .requires_grad为True，那么他会自动跟踪对于该张量的所有操作。当完成计算后可以通过调用.backward()，来自动计算所有的梯度。这个张量的所有梯度会自动累加到.grad属性。

　　注：在 y.backward() 时，如果 y 是标量，则不需要为 backward() 传入任何参数；否则，需要传入一个与 y 同形的Tensor。

　　要阻止一个张量被跟踪历史，可以调用.detach()方法将其与计算历史分离，并阻止它未来的计算记录被跟踪。为了防止跟踪历史记录（和使用内存），可以将代码包装在

with torch.no_grad(): 中。这在评估模型时非常有用，因为模型可能具有 requires_grad = True的可训练参数，但是不要在此过程中对其进行梯度计算。

　　还有一个类对于autograd的实现非常重要：Function。Tensor 和 Function 互相连接生成了一个无环图 (acyclic graph)，它编码了完整的计算历史。每个张量都有一个.grad_fn属性，该属性引用了创建 Tensor 自身的Function(除非这个张量是用户手动创建的，即这个张量的grad_fn是 None )。下面给出的例子中，张量由用户手动创建，因此grad_fn返回结果是None。

from __future__ import print_function
import torch
x = torch.randn(3,3,requires_grad=True)
print(x.grad_fn)

输出：
None

　　如果需要计算导数，可以在 Tensor 上调用 .backward()。

　　如果Tensor 是一个标量(即它包含一个元素的数据），则不需要为 backward()指定任何参数，但是如果它有更多的元素，则需要指定一个gradient参数，该参数是形状匹配的张量。

　　创建一个张量并设置requires_grad=True用来追踪其计算历史

x = torch.ones(2, 2, requires_grad = True)
print(x)

输出：

tensor([[1., 1.],
        [1., 1.]], requires_grad=True)

## 对这个张量做一次运算：

y = ** 2
print(y)

输出：

tensor([[1., 1.],
        [1., 1.]], grad_fn=<PowBackward0>)

# y是计算的结果，所以它有grad_fn属性。

print(y.grad_fn)

输出：

<PowBackward0 object at 0x000001CB45988C70>

## 对 y 进行更多操作

z = y * y * 3
out = z.mean()
print(z,out)

输出：

tensor([[3., 3.],
        [3., 3.]], grad_fn=<MulBackward0>) tensor(3., grad_fn=<MeanBackward0>)

　　.requires_grad(...)原地改变了现有张量的requires_grad标志。若无指定，默认为False。

a = torch.randn(2, 2) # 缺失情况下默认 requires_grad = False
a = ((a * 3) / (a - 1))
print(a.requires_grad)
a.requires_grad_(True)
print(a.requires_grad)
b = (a * a).sum()
print(b.grad_fn)

输出：

False
True
<SumBackward0 object at 0x000001CB4A19FB50>

2.2.1 梯度

　　现在开始进行反向传播：out是一个标量，所以out.backward()和out.backward(torch.tensor(1.))等价。

out.backward()
# 输出导数d(out)/dx
print(x.grad)

输出：

tensor([[3., 3.],
        [3., 3.]])

　　

 

 

 　　注：grad在反向传播过程中是累加的，每一次运行反向传播，梯度都会累加之前的梯度，所以在反向传播前需要进行梯度清零操作。

# 再来反向传播⼀一次，注意grad是累加的
out2 = x.sum()
out2.backward()
print(x.grad)

输出：

tensor([[4., 4.],
        [4., 4.]])

out3 = x.sum() 
x.grad.data.zero_() 
out3.backward() 
print(x.grad)

输出：

tensor([[1., 1.],
        [1., 1.]])

　　一个雅可比向量积的例子：

x = torch.randn(3, requires_grad=True)
print(x)

y = x * 2
i = 0
while y.data.norm() < 1000:
    y = y * 2
    i = i + 1
print(y)
print(i)

输出：

tensor([-0.9332,  1.9616,  0.1739], requires_grad=True)
tensor([-477.7843, 1004.3264,   89.0424], grad_fn=<MulBackward0>)
8

　　在这种情况下，y不再是标量。torch.autograd 不能直接计算完整的雅可比矩阵，但是如果我们只想要雅可比向量积，只需将这个向量作为参数传给 backward：

v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
y.backward(v)
print(x.grad)

输出：

tensor([5.1200e+01, 5.1200e+02, 5.1200e-02])

　　也可以通过将代码块包装在with torch.no_grad(): 中，来阻止 autograd 跟踪设置了.requires_grad=True的张量的历史记录。

print(x.requires_grad)
print((x ** 2).requires_grad)

with torch.no_grad():
    print((x ** 2).requires_grad)

输出：

True
True
False

　　如果我们想要修改 tensor 的数值，但是又不希望被 autograd 记录(即不会影响反向传播)， 那么我们可以对 tensor.data 进行操作。

x = torch.ones(1,requires_grad=True)

print(x.data) # 还是一个tensor
print(x.data.requires_grad) # 但是已经是独立于计算图之外

y = 2 * x
x.data *= 100 # 只改变了值，不会记录在计算图，所以不会影响梯度传播

y.backward()
print(x) # 更改data的值也会影响tensor的值 
print(x.grad)

输出：

tensor([1.])
False
tensor([100.], requires_grad=True)
tensor([2.])

2.3 并行计算简介

　　.cuda()是让我们的模型或者数据从CPU迁移到GPU(0)当中，通过GPU开始计算。

　　注：

1. 我们使用GPU时使用的是.cuda()而不是使用.gpu()。这是因为当前GPU的编程接口采用CUDA，但是市面上的GPU并不是都支持CUDA，只有部分NVIDIA的GPU才支持，AMD的GPU编程接口采用的是OpenCL，在现阶段PyTorch并不支持。

2. 数据在GPU和CPU之间进行传递时会比较耗时，我们应当尽量避免数据的切换。

3. GPU运算很快，但是在使用简单的操作时，我们应该尽量使用CPU去完成。

4. 当我们的服务器上有多个GPU，我们应该指明我们使用的GPU是哪一块，如果我们不设置的话，tensor.cuda()方法会默认将tensor保存到第一块GPU上，等价于tensor.cuda(0)，这将会导致爆出out of memory的错误。我们可以通过以下两种方式继续设置。

　　方法1：

 #设置在文件最开始部分
import os
os.environ["CUDA_VISIBLE_DEVICE"]="2"# 设置默认的显卡

　　方法2：

CUDA_VISBLE_DEVICE=0,1 python train.py# 使用0，1两块GPU

2.3.1 常见的并行的方法

　　网络结构分布到不同的设备中(Network partitioning)

　　主要的思路：将一个模型的各个部分拆分，然后将不同的部分放入到GPU来做不同任务的计算。

 

 

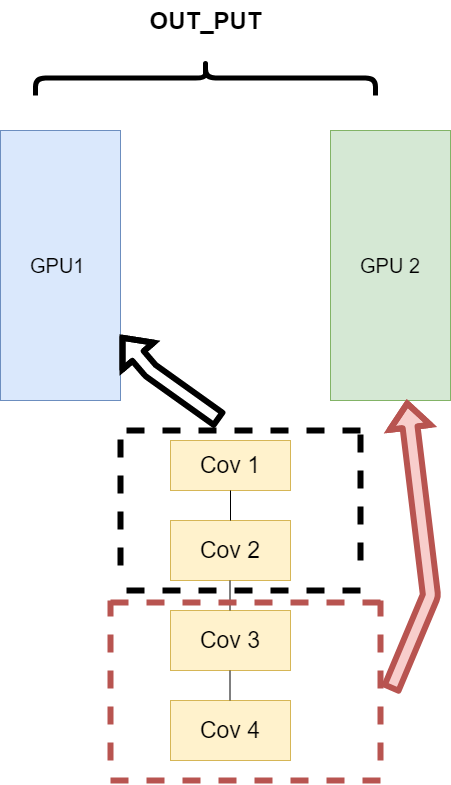
　　 缺点：不同模型组件在不同的GPU上时，GPU之间的传输就很重要，对于GPU之间的通信是一个考验。但是GPU的通信在这种密集任务中很难办到，所以这个方式慢慢淡出了视野。

　　同一层的任务分布到不同数据中(Layer-wise partitioning)

　　思路：同一层的模型做一个拆分，让不同的GPU去训练同一层模型的部分任务

　　

 

 

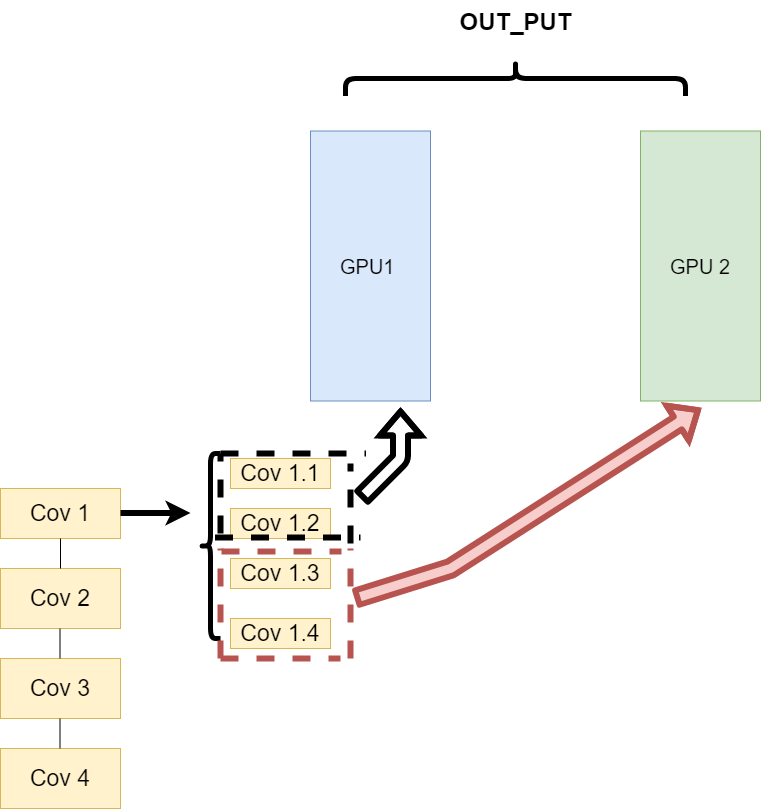
 　　这样可以保证在不同组件之间传输的问题，但是在我们需要大量的训练，同步任务加重的情况下，会出现和第一种方式一样的问题。

　　不同的数据分布到不同的设备中，执行相同的任务(Data parallelism)（主流方法）

　　逻辑：我不再拆分模型，我训练的时候模型都是一整个模型。但是我将输入的数据拆分。

　　所谓的拆分数据就是，同一个模型在不同GPU中训练一部分数据，然后再分别计算一部分数据之后，只需要将输出的数据做一个汇总，然后再反传。

　　其架构如下：

　　

 

 

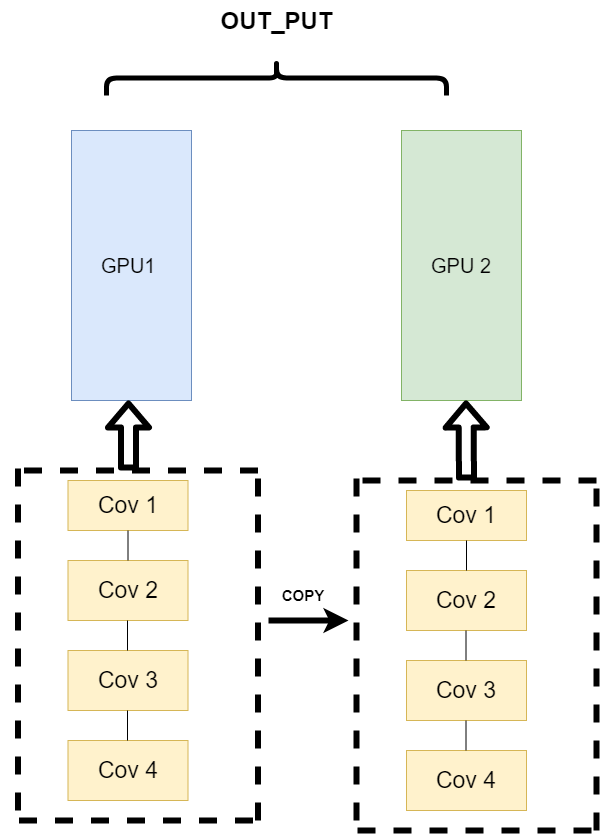
 　　这种方式可以解决之前模式遇到的通讯问题。现在的主流方式是数据并行的方式(Data parallelism)