python第九章课后习题
9.2某车间生产滚珠,随机的抽出了50粒,测得他们的直径为(单位mm)15.0 15.8 15.2 15.1 15.9 14.7 14.8 15.5 15.6 15.3 15.1 15.3 15.0 15.6 15.7 14.8 14.5 14.2 14.9 14.9 15.2 15.0 15.3 15.6 15.1 14.9 14.2 14.6 15.8 15.2 15.9 15.2 15.0 14.9 14.8 14.5 15.1 15.5 15.5 15.1 15.1 15.0 15.3 14.7 14.5 15.5 15.0 14.7 14.6 14.2 通过计算得到样本均值为15.0780,样本标准差为0.4325,试问滚珠直径是否服从正态分布
点击查看代码
from scipy.stats import shapiro
data = [15.0, 15.8, 15.2, 15.1, 15.9, 14.7, 14.8, 15.5, 15.6, 15.3,
15.1, 15.3, 15.0, 15.6, 15.7, 14.8, 14.5, 14.2, 14.9, 14.9,
15.2, 15.0, 15.3, 15.6, 15.1, 14.9, 14.2, 14.6, 15.8, 15.2,
15.9, 15.2, 15.0, 14.9, 14.8, 14.5, 15.1, 15.5, 15.5, 15.1,
15.1, 15.0, 15.3, 14.7, 14.5, 15.5, 15.0, 14.7, 14.6, 14.2]
stat, p = shapiro(data)
print(f"Shapiro-Wilk Statistic: {stat}")
print(f"P-value: {p}")
alpha = 0.05
if p > alpha:
print("滚珠直径数据服从正态分布N(15.0780, 0.4325^2)")
else:
print("滚珠直径数据不服从正态分布N(15.0780, 0.4325^2)。")
print("学号:2023310143028")

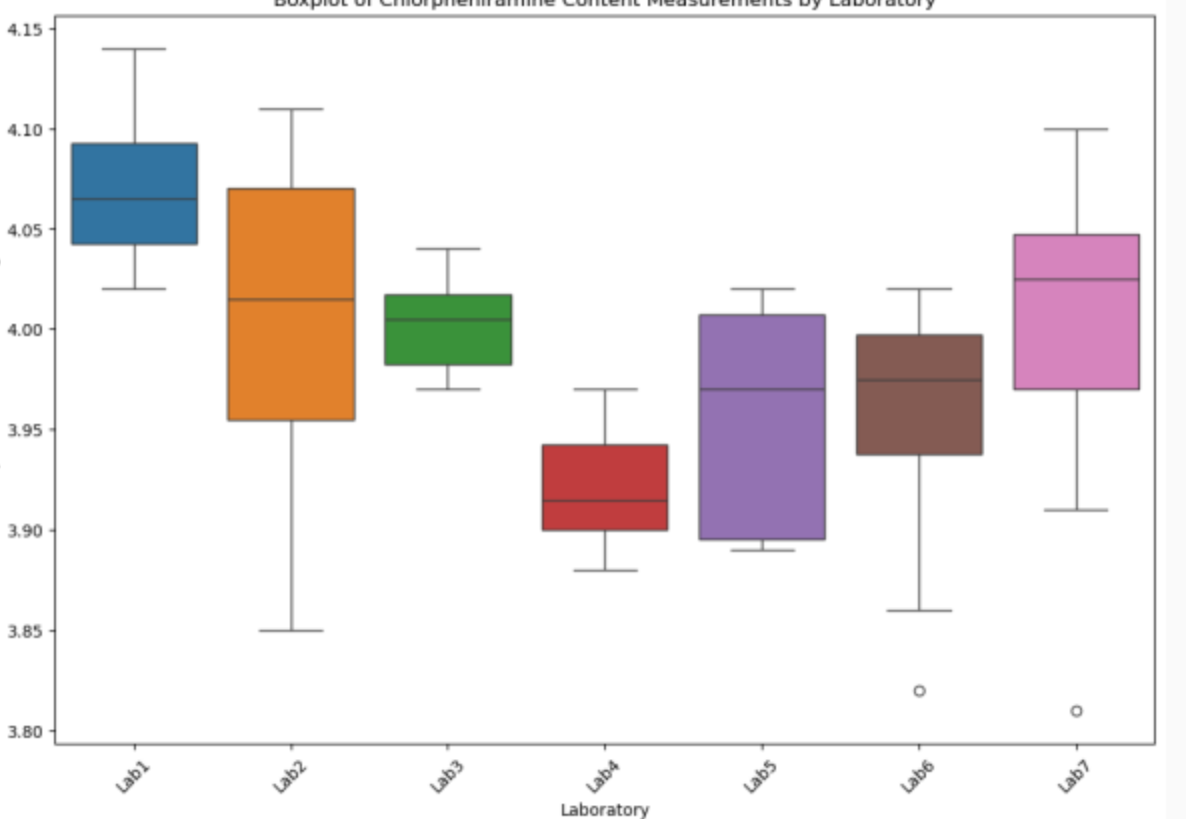
9.3 在7个不同实验室中测量某种扑尔敏药片的扑尔敏有效含量(以mg计),得到结果如表格(读取外部表格excel文件,第一行为实验室Lab1到Lab7,每一列下面为有效含量)。画出各实验室测量结果的箱线图,设各样本分布来自正态总体N(μi,σ^2)i为μ的下标,i=1,2,...,7,各样本相互独立,试取显著水平α=0.05检验各实验室测量的扑尔敏的有效含量的
点击查看代码
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
file_path = '9.3.xlsx'
data = pd.read_excel(file_path, header=0)
labs = ['Lab1', 'Lab2', 'Lab3', 'Lab4', 'Lab5', 'Lab6', 'Lab7']
assert all(lab in data.columns for lab in labs), "Excel文件中的列名与实验室名称不匹配"
plt.figure(figsize=(12, 8))
sns.boxplot(data=data)
plt.xticks(rotation=45)
plt.title('Boxplot of Chlorpheniramine Content Measurements by Laboratory')
plt.xlabel('Laboratory')
plt.ylabel('Chlorpheniramine Content (mg)')
plt.show()
f_stat, p_value = stats.f_oneway(data['Lab1'], data['Lab2'], data['Lab3'], data['Lab4'], data['Lab5'], data['Lab6'], data['Lab7'])
print(f"F-statistic: {f_stat}")
print(f"P-value: {p_value}")
alpha = 0.05
if p_value < alpha:
print("在显著水平α=0.05下,各实验室测量的扑尔敏有效含量的均值有显著差异。")
else:
print("在显著水平α=0.05下,各实验室测量的扑尔敏有效含量的均值没有显著差异。")
print("学号:2023310143028")
9.4
点击查看代码
from scipy.stats import f_oneway
data = [
[173, 172, 173, 174, 176, 178, 177, 179, 176, 172, 173, 174],
[175, 173, 176, 178, 177, 179, 174, 175, 173, 170, 171, 172],
[177, 175, 176, 174, 174, 175, 174, 173, 174, 169, 169, 170]
]
A1 = data[0][:3] + data[1][3:6] + data[2][6:9]
A2 = data[0][3:6] + data[1][6:9] + data[2][9:12]
A3 = data[0][6:9] + data[1][9:12] + data[2][:3]
B1 = data[0][:3] + data[0][3:6] + data[0][6:9]
B2 = data[1][:3] + data[1][3:6] + data[1][6:9]
B3 = data[2][:3] + data[2][3:6] + data[2][6:9]
B4 = [data[0][9:12], data[1][9:12], data[2][9:12]]
B4 = [item for sublist in B4 for item in sublist]
# 品种因素
f_value_variety, p_value_variety = f_oneway(A1, A2, A3)
# 化肥因素
f_value_fertilizer, p_value_fertilizer = f_oneway(B1, B2, B3, B4)
print("品种因素:")
print("F值:", f_value_variety)
print("P值:", p_value_variety)
print("化肥因素:")
print("F值:", f_value_fertilizer)
print("P值:", p_value_fertilizer)
print("3028")
print("学号:2023310143028")

9.5 某集团为研究商品销售点所在的地理位置、销售点处的广告、销售点的装横这3个因素对商品的影响度,选了3个位置,2种广告形式,2种装横档次在4个城市进行了搭配实验,如表中所示,试在显著水平0.05下,检验不同地理位置、不同广告、不同装横下的销售量是否有显著差异?
点击查看代码
import statsmodels.api as sm
a=np.loadtxt('ti9_5.txt').T
x1 = np.tile(np.hstack([np.ones(4), 2 * np.ones(4), 3 * np.ones(4)]), (4, 1)).flatten()
x2 = np.tile(np.tile([1, 1, 2, 2], (1, 3)), (4, 1)).flatten()
x3 = np.tile(np.tile([1, 2], (1, 6)), (4, 1)).flatten()
d = {'x1':x1, 'x2':x2, 'x3':x3,'y':a.flatten()}
md = sm.formula.ols('y~C(x1) * C(x2) * C(x3)', d).fit()
ano = sm.stats.anova_lm(md)
print(ano)
print('总偏差平方和:', sum(ano.sum_sq))
print("学号:2023310143028")
结果:
df sum_sq mean_sq F PR(>F)
C(x1) 2.0 38195.791667 19097.895833 52.174104 2.310582e-11
C(x2) 1.0 18565.333333 18565.333333 50.719180 2.274230e-08
C(x3) 1.0 10034.083333 10034.083333 27.412408 7.298787e-06
C(x1):C(x2) 2.0 3466.541667 1733.270833 4.735174 1.493950e-02
C(x1):C(x3) 2.0 1326.541667 663.270833 1.812009 1.779065e-01
C(x2):C(x3) 1.0 90.750000 90.750000 0.247923 6.215698e-01
C(x1):C(x2):C(x3) 2.0 1191.125000 595.562500 1.627035 2.106302e-01
Residual 36.0 13177.500000 366.041667 NaN NaN
总偏差平方和: 86047.66666666663



 浙公网安备 33010602011771号
浙公网安备 33010602011771号