组合计数

组合计数

递推

用递推的方式来维护信息

一般直接没法下手的时候，考虑不重不漏划分成子问题然后考虑，一般可以按照最后一个什么什么划分。

隔板法

对于一些分配性的问题，转化成小球问题，用隔板去分配

例如: $x_1+x_2+...+x_k==n$求正整数$x$的解。

等价于$n$个小球分成$k$组，也就是$c_{n-1}^{k-1}$

对于等式我们可以用$k-1$个隔板把所有小球分成$k$部分

对于不等式我们可以用$k$个隔板把小球分成$k+1$个部分，取前$k$个部分当成有贡献的即可

加法原理 乘法原理

乘法：乘法分步，步步相关 每一步都必不可缺

加法：确定工作的分类方法，每一种方法都可以完成任务

组合数 排列数

组合数公式： $c_{n}^{m}=\frac{n!}{m!*(n-m)!}$

排列数公式：$p_{n}^{m}=\frac{n!}{(n-m)!}$

区别在于选取的那$m$个数本身是否有区别，进一步来看在于选的东西是否区别于顺序

递推法

前$n$个里选$m$个等价于最后一个选不选(选：前$n-1$个里选$m-1$个、不选：前$n-1$个里选$m$个)

$c_{n}^m=c_{n-1}+c_{n-1}^{m}$

复杂度$O(n^2)$

 for (int i = 0; i < 2010; i ++ )
        for (int j = 0; j <= i; j ++ )
            if (j) c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
            else c[i][j] = 1;

数据范围较小的时候方便

公式法

依照 $c_{n}^{m}=\frac{n!}{m!*(n-m)!}$，算出阶乘即可。

因为设涉及到除法取模，因此我们要求一下逆元

费马小定理

若p是质数且(a,p)==1，则有$a^{p-1}\equiv1(mod\ p)$

乘法逆元

若$\frac{a}{b}\equiv a*x(mod\ p)$，因为除法无法直接取模

称x为b的乘法逆元，$x=b^{-1}$

即$b*b^{-1}\equiv1(mod\ p)$

由费马小定理

$a*a^{p-2}\equiv1(mod\ p)$

故a乘法逆元为$a^{p-2}$

我们预处理出来乘法逆元以后直接套组合数公式即可。

复杂度$O(a*log(mod))$

int qmi(int a,int b, int p) {
	int res = 1;
	while (b) {
		if (b & 1) res = (LL)res * a % p; // 防止爆精度 
		a = (LL)a * a % p;
		b >>= 1;
	}
	return res;
}

fact[0] = infact[0] = 1;
	for (int i = 1; i < N; i ++ ) {
		fact[i] = (LL) fact[i - 1] * i % mod;
		infact[i] = (LL) infact[i - 1] * qmi(i, mod - 2, mod) % mod;// i 的乘法逆元 
	}

算法瓶颈在求逆元用到了快速幂

线性求逆元

设要求i在模p意义下的逆元，设$p=k\times i+r$

则有 $k\times i + r\equiv 0(mod\ p)$

$k\times r^{-1}+i\equiv0(mod\ p)$

$i^{-1}\equiv -k\times r^{-1}$

$k=\lfloor \frac{p}{i}\rfloor$、$r=p\ mod\ i$

所以$i^{-1}\equiv-\lfloor \frac{p}{i}\rfloor\times(p\ mod\ i)^{-1}(mod\ p)$

infact[0]=infact[1]=1;
for (int i = 2; i < N; i ++ )
    infact[i]=(LL)(mod - mod / i) * infact[mod % i] % mod;
for (int i = 2; i < N; i ++ )
    infact[i] = (LL)infact[i] * infact[i - 1] % mod;

这样就可以优化到$O(n)$

扩展欧几里得求逆元

如果a,p互质则可以有$ax+py\equiv1(modp)$，通过exgcd求出一个$x_0$,

通解为$x=x_0+kb/(a,b)$

然后对于$x_0$找到一个正的解即可也就是$(x % p+p)%p$

Lucas

解决$a,b过大但是模数p不大的情况$

复杂度在$O(log_{p}^Nplogp)$

证明链接:[Link](AcWing 887. 求组合数 III(lucas定理) - AcWing)

公式：

$c_{a}^{b}\equiv c_{amodp}^{bmodp}\times c_{a/p}^{b/p}(mod\ p)$

意义就是对于太大的没法算的转化为有个在可以算的范围内的数了。

int qmi(int a, int b, int p) {
    int res = 1;
    while (b) {
        if (b & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        b >>= 1;
    }
    return res;
}
int C(int a, int b, int p) {
    int res = 1;
    for (int i = 1, j = a; i <= b; i ++, j --) {
        res = (LL) res * j % p;
        res = (LL) res * qmi(i, p - 2, p) % p;
    }
    return res;
}
int Lucas(LL a, LL b, int p) {
    if (a < p && b < p) return C(a, b, p);
    return (LL)C(a % p, b % p, p) * Lucas(a / p, b / p, p) % p;
}

高精度计算

对于一些不取模的组合数，需要用到高精度计算

因为是个整数，所以我们可以筛出公式中所有的质因子，上下相消

最后就是一堆质因子的乘积，因为太大了，所以用高精度乘法计算即可。

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <set>
#include <queue>
#include <vector>
#include <map>
#include <bitset>
#include <unordered_map>
#include <cmath> 
#include <stack>
#include <iomanip>
#include <deque> 
#include <sstream>
#define x first
#define y second
#define debug(x) cout<<#x<<":"<<x<<endl;
using namespace std;
typedef long double ld;
typedef long long LL;
typedef pair<int, int> PII;
typedef pair<double, double> PDD;
typedef unsigned long long ULL;
const int N = 1e5 + 10, M = 2 * N, INF = 0x3f3f3f3f, mod = 1e9 + 7;
const double eps = 1e-8, pi = acos(-1), inf = 1e20;
#define tpyeinput int
inline char nc() {static char buf[1000000],*p1=buf,*p2=buf;return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++;}
inline void read(tpyeinput &sum) {char ch=nc();sum=0;while(!(ch>='0'&&ch<='9')) ch=nc();while(ch>='0'&&ch<='9') sum=(sum<<3)+(sum<<1)+(ch-48),ch=nc();}
int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};
int h[N], e[M], ne[M], w[M], idx;
void add(int a, int b, int v = 0) {
    e[idx] = b, w[idx] = v, ne[idx] = h[a], h[a] = idx ++;
}
int n, m, k;
int a[N];
int primes[N], cnt;
int sum[N];
bool st[N];

void get_primes(int n) {
    for (int i = 2; i <= n; i ++) {
        if (!st[i]) primes[cnt ++] = i;
        for (int j = 0; primes[j] <= n / i; j ++) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}
int get(int n, int p) {
    int res = 0;
    while (n) {
        res += n / p;
        n /= p;
    }
    return res;
}
vector<int> mul(vector<int> a, int b) {
    vector<int> c;
    int t = 0;
    for (int i = 0; i < a.size(); i ++ ) {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }
    while (t) c.push_back(t % 10), t /= 10;
    return c;
}
int main() {
    ios::sync_with_stdio(false), cin.tie(0);
    int a, b; cin >> a >> b;
    get_primes(a);
    for (int i = 0; i < cnt; i ++ ) {
        int p = primes[i];
        sum[i] = get(a, p) - get(b, p) - get(a - b, p);
    }
    vector<int> res;
    res.push_back(1);
    for (int i = 0; i < cnt; i ++ )
        for (int j = 0; j < sum[i]; j ++ )
            res = mul(res, primes[i]);
    for (int i = res.size() - 1; i >= 0; i --) cout << res[i];
    cout << endl;
    return 0;
}

卡特兰数

给定 $n$ 个 $0$ 和 $n$ 个 $1$，它们将按照某种顺序排成长度为 $2n$ 的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中 $0$ 的个数都不少于 $1$ 的个数的序列有多少个

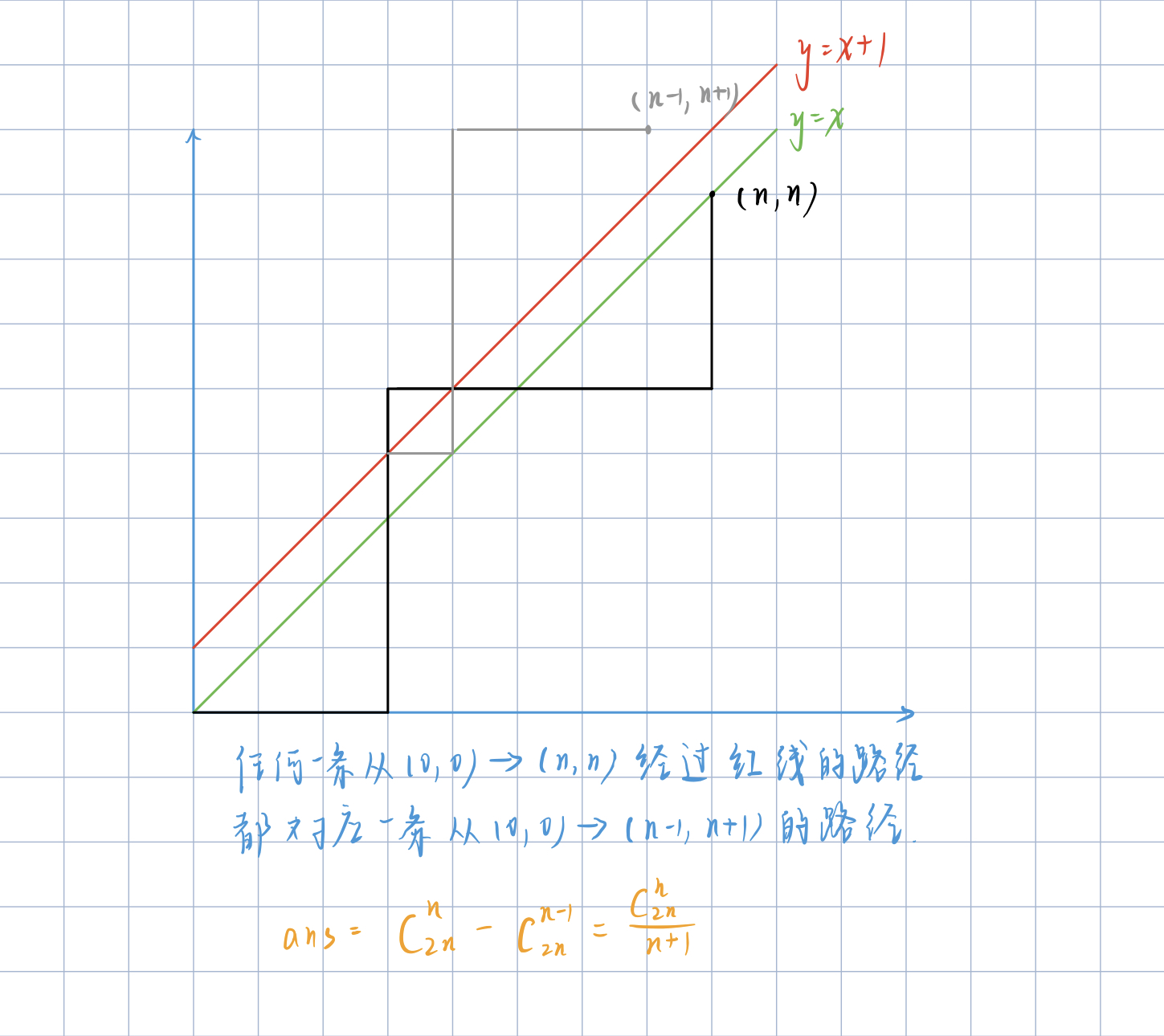
设为0为向右走1为向上走，问题转化为从$(0,0)$走到$(n,n)$的合法路径，利用容斥原理总的减去不合法的就是答案。

任意一条不合法的路径，我们取第一次和红线相交的位置对称过去，发现都会走到$(n-1,n+1)$这个点，因此走到$(n-1,n+1)$的方案数于不合法的方案数一一对应。

任意一个点$(n,m)$对应的答案为$C_{n+m}^n-C_{n+m}$

$(n,m)$对称过去$(m-1,n+1)$

如何挖掘是卡特兰数

1. 满足递推式(代表问题：求二叉树个数) $f(n)=f(1)f(n-1)+f(2)f(n-2)$

2. 挖掘性质：任意前缀中某种东西的个数$\ge$另一种东西的个数