UCB-CS170 笔记

图论

pre 和 post

记录一下一个OI中没怎么学会的知识点

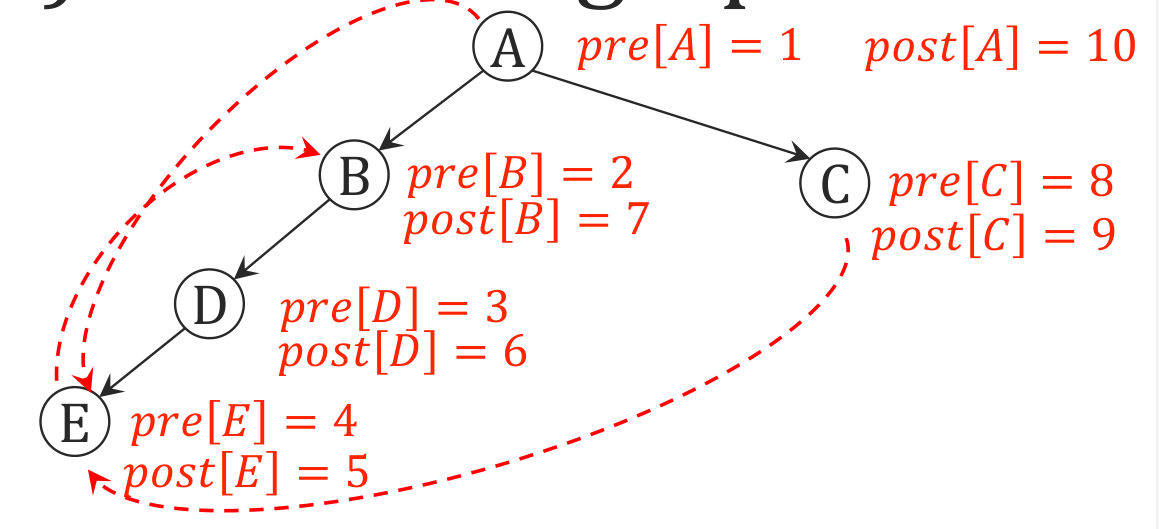
上图是一个DFS遍历，pre数组记录了每个节点最初被访问的时间，post数组记录了每个节点最后被访问的时间(进出栈的时间)

根据两个数组，可以将所有边分为四类

• 树边(Tree Edge): DFS 树中的边
• 后向边(Back Edge): 从一个节点到其祖先的边
• 前向边(Forward Edge): 从一个节点到其子孙(非直接)的边
• 横叉边(Cross Edge): 除了上述三种边之外的边(在 DFS 树中要先往上再往下)
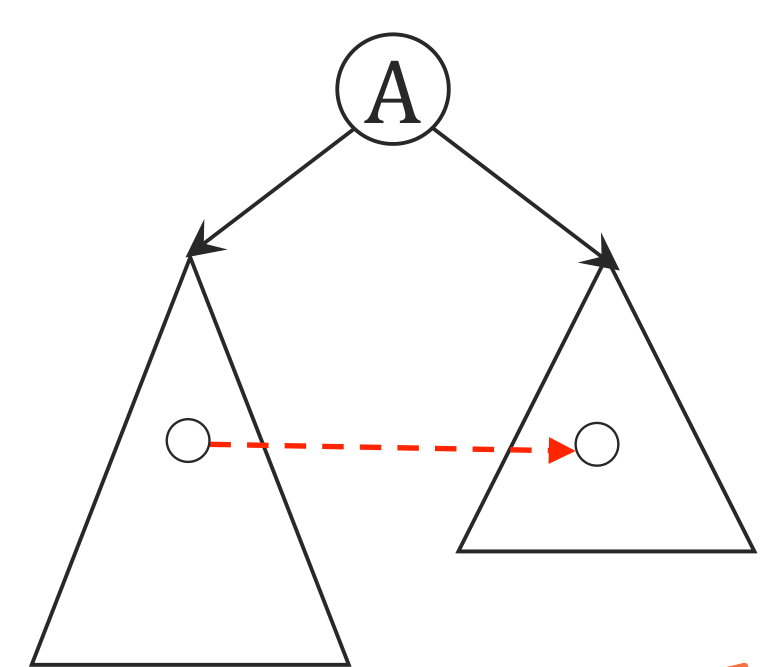
  • 注意横叉边肯定是从右往左的，否则如下图，虚线边会先被访问，就不是横叉边而是树边了
  • 这也意味着无向图不会有横叉边
  • 

它们的性质如下

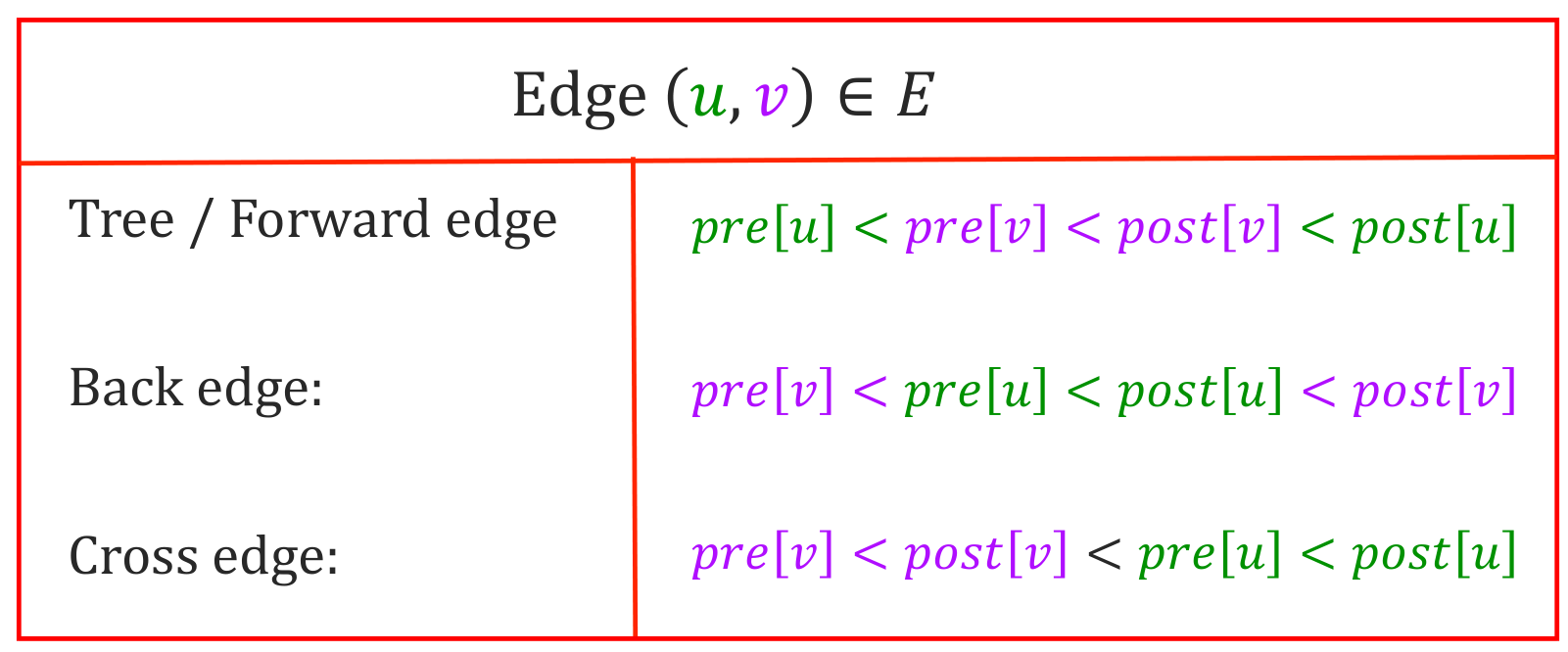
边分类的代码：

def categorize_edges(adj_list):
    """
    args:
        adj_list:List[List[int]] = the adjacency list that represents our input graph
    return:
        Dictionary({
            'tree': set(),
            'forward': set(),
            'cross': set(),
            'back': set()  
        }) where each set() contains the edges that belong to the corresponding edge type
    """
    edges_lookup = {
        'tree': set(),
        'forward': set(),
        'cross': set(),
        'back': set()
    }
    
    prev = dfs(adj_list)
    pre_order, post_order = get_pre_post(adj_list)

    pre, post = {}, {}
    for node, pre_time in pre_order:
        pre[node] = pre_time
    for node, post_time in post_order:
        post[node] = post_time

    n = len(adj_list)
    for u in range(n):
        for v in adj_list[u]:
            if pre[u] < pre[v] and post[v] < post[u]:
                if prev[v] == u:
                    edges_lookup['tree'].add((u, v))
                else:
                    edges_lookup['forward'].add((u, v))
            elif pre[v] < pre[u] and post[u] < post[v]:
                edges_lookup['back'].add((u, v))
            else:
                edges_lookup['cross'].add((u, v))

    
    return edges_lookup

Kosaraju 算法

给定一个图 \(G = (V, E)\)，考虑如何求出它的强连通分量(SCC)

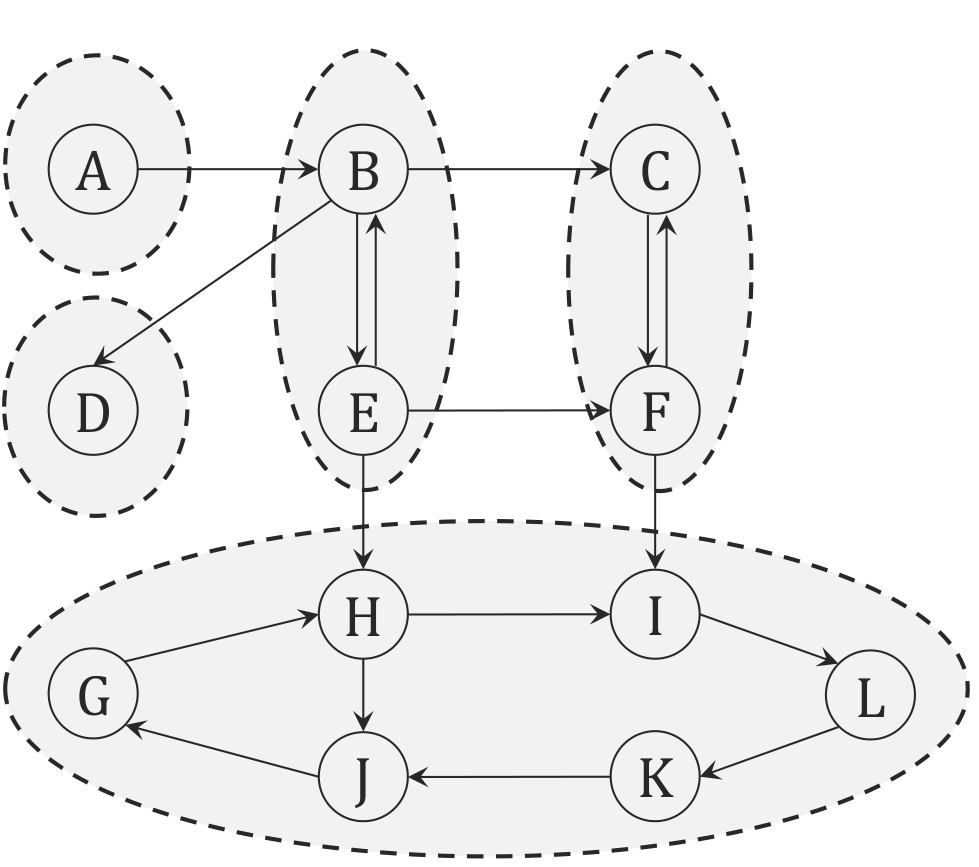
如上图，如果我们将其看成一个由 SCC 构成的 DAG，在叶节点进行一次 DFS 找到所有能访问到的节点，就是一个 SCC(因为叶节点只进不出)，然后删去这个叶节点，依次类推。

所以我们只需要设计一个算法，使得他能够“倒序”访问这些节点即可

我们考虑使用之前定义的 post 数组，如果在 \(G\) 中有从强连通分量 \(C\) 到 \(C'\) 的边，那么 \(C\) 中的最大 post 数一定大于 \(C'\) 中的最大 post 数，所以最大的 post 数对应的节点一定是源(source)

我们定义图的转置 \(G^T = (V, E^T)\), 其中 \(E^T = \{(u, v) | (v, u) \in E\}\)，通俗的说就是将所有边的方向反过来，那么在 \(G^T\) 中，最大的 post 数对应的节点一定是 \(G\) 中的汇(sink)，从大到小依次是原图中汇到源的拓扑序

1. 在 $ G^T $ 上运行 DFS, 得到每个节点的 post
2. 在 $ G $ 上运行 DFS, 按照 post 从大到小的顺序访问节点，每次访问到的节点都是一个 SCC

代码如下

def find_SCCs(adj_list):
    """
    args:
        adj_list:List[List[int]] = the adjacency list that represents our input graph
    return:
        List(Set(int, ...), ...) a list of sets where each set contains all the nodes 
            that belong to the corresponding SCC
    """
    scc_list = []
    n = len(adj_list)
    reverse_adj_list = reverse_graph(adj_list)
    _, post_order = get_pre_post(reverse_adj_list)
    visited = [False] * n
    post_order.sort(key=lambda x: x[1], reverse=True)
    for u, _ in post_order:
        if not visited[u]:
            scc = set()
            stack = [u]
            while stack:
                u = stack.pop()
                if not visited[u]:
                    visited[u] = True
                    scc.add(u)
                    for v in adj_list[u]:
                        stack.append(v)
            scc_list.append(scc)
    return scc_list

HW4Q4 半联通

对于一个有向无环图，定义半联通性(semiconnectivity)为：对于任意两个节点 \(u, v\)，存在一条从 \(u\) 到 \(v\) 的路径或者从 \(v\) 到 \(u\) 的路径。求证：对于一个有向无环图，它是半联通的充要条件是存在一条可以访问到所有节点的路径

充分性显然，下证必要性
对于这个有向无环图，可以进行拓扑排序，得到一个拓扑序列 \(v_1, v_2, \cdots, v_n\)，因为有向无环，所以没有后向边，考虑拓扑序列中的任意点对 \(v_i, v_{i+1}\)，只能存在 \(v_i \rightarrow v_{i+1}\) 的边，否则 \(v_{i+1}\) 就会有 \(v_i\) 的后向边，所以 \(v_i\) 到 \(v_{i+1}\) 有一条路径，那么我们就找到了一条从 \(v_1\) 到 \(v_n\) 的路径

HW4Q5 2-SAT问题

一个2-SAT问题是指，给定一个布尔表达式，其中每个子句都是两个文字的析取，求是否存在一种赋值方式使得表达式为真。例如，\((x_1 \vee x_2) \wedge (\neg x_1 \vee x_3) \wedge (\neg x_2 \vee \neg x_3)\)。

建图

把合取转化为蕴含，然后把蕴含转化为边，最后把每个文字转化为两个点，分别表示自身和否定(如 \(x_1\) 和 \(\neg x_1\))，然后把蕴含转化为边，如 \((x_1 \vee x_2)\) 转化为 \((\neg x_1 \rightarrow x_2) \wedge (\neg x_2 \rightarrow x_1)\)，然后把蕴含转化为边

获得答案

2-SAT 问题有解等价于图中不存在 \(x\) 和 \(\neg x\) 在同一个强连通分量中，因为如果存在这样的强连通分量，那么就有 \(x \rightarrow \neg x\) 和 \(\neg x \rightarrow x\)，所以 \(x\) 和 \(\neg x\) 不能同时为真，所以没有解
反之如果不存在这样的强连通分量，那么就可以按拓扑序列从后往前赋值即可(注意，赋值一个文字的否定为真意味着将其赋值为假)，对一个 SCC 赋值完之后考虑它的父 SCC

HW6Q3 最小 \(\infty\)-范数割集

给定一个无向连通图，求一个割集，使得割集中的边的 \(\infty\)-范数最小，即 \(\max_{e \in E'} w(e)\) 最小，其中 \(E'\) 是割集中的边，\(w(e)\) 是边 \(e\) 的权重。要求复杂度为 \(O(|E| \log |V|)\)

翻译一下就是最大边权最小。一个简单的方法是对边权二分。但是在这里详细分析一下另外一种利用 MST 的 Cut Property 的方法，就是先求出一个 MST，然后对于 MST 中最小的那条边，输出这条边对应的 MST 中的割集即可。

正确性证明

先复习一下 Cut Property: 对于一个无向连通图 \(G = (V, E)\)，对于任意一个割集 \(E'\)，如果 \(e\) 是 \(E'\) 中的最小边，那么 \(e\) 一定属于 \(G\) 的某个最小生成树

此外我们需要一个性质: 一个图的两棵最小生成树，边的权值序列排序后结果相同

• 证明: 设最小生成树有n条边，任意两棵最小生成树分别称为A, B，其中A 的边权递增排序为 \(a_1, a_2, \cdots, a_n\)，B 的边权递增排序为 \(b_1, b_2, \cdots, b_n\)
  假设在第 \(i\) 个位置 \(a_i \neq b_i\)，不妨设 \(w(a_i) \geq w(b_i)\)
  • 如果 A 中包含 \(b_i\)，则必存在 \(j\) 使得 \(w(a_j) = w(b_i)\)，那么 \(w(a_i) \geq w(b_i) = w(a_j) \geq w(a_i)\)，它们边权都相等，调换一下顺序也不影响
  • 如果 A 中不包含 \(b_i\)，那么把 \(b_i\) 加入 A 中，必然会形成一个环，环中的边权都不大于 \(w(b_i)\)。另一方面，B 不可能覆盖整个环，必有某条边是仅仅属于 A 而不属于 B 的(这意味着不是前面的公共部分)，设为 \(a_j\)，那么 \(w(a_j) \leq w(a_i) \leq w(b_i) = w(a_j)\)，它们边权都相等，调换一下顺序也不影响

有了这两个性质，原算法的正确性几乎是显然的

贪心算法

Horn-SAT

定义: 一个 Horn-SAT 公式是一个由 Horn 子句构成的公式, 其中 Horn 子句是至多有一个正文字(positive literal)的合取范式

一共只有两种: \(\neg x_1 \vee \neg x_2 \vee \cdots \vee \neg x_i\) 和 \(\neg x_1 \vee \neg x_2 \vee \cdots \vee \neg x_j \vee x_{j+1}\)
其中后者可以写成蕴含形式: $ (x_1 \wedge x_2 \wedge \cdots \wedge x_j) \rightarrow x_{j+1}$

算法很简单，一开始所有变量都为假，然后每次都看哪个蕴含式的前提都为真，就把它的结论设为真。一开始只有单个变量的"蕴含式"(没有前提)会被考虑，后面就是看哪些前提一定满足，就把结论设为真

近似算法

近似算法中一个重要的定义是近似比(approximation ratio): 一个算法的解与最优解的比值

一般贪心算法都是比较优秀的近似算法, 如

集合覆盖问题

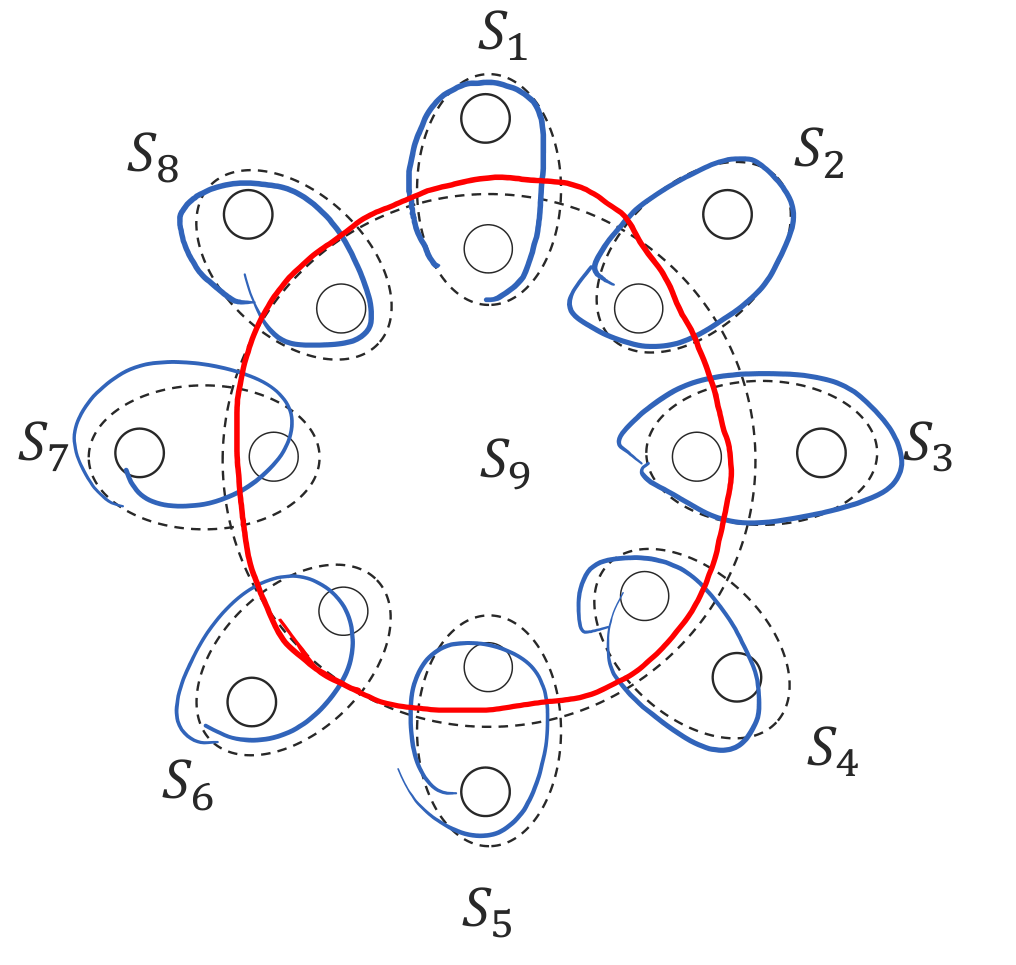
一个最直观的想法就是每次选能覆盖最多的集合，这显然不是最优(如上图)，但是可以证明它的近似比为 \(ln n\)

• 事实上如果最优解的集合数为 \(k\), 那么根据平均数原理, 至少有一个集合覆盖了 \(\dfrac{n}{k}\) 个元素, 每次选覆盖最多的集合可以使得原集合的大小缩减到之前的 \(\dfrac{k-1}{k}\), 经过 \(k \ln n\) 次迭代后, 剩下的集合数为 \(1\)

HW6Q4 Firefighters

有一颗 \(N\) 个节点的树，可以建造 \(K\) 个消防站，定义，某个消防站的响应时间为其到树上任意一个节点的最大距离，所有消防站的响应时间是他们个别的响应时间的最大值。考虑一个贪心算法，每次在距离当前消防站最远的节点建造消防站，证明这个算法的近似比为 \(2\)

证明

设最优解的响应时间为 \(R_{opt}\)，贪心算法的响应时间为 \(R_{greedy}\)，那么我们可以得出一个重要性质就是对贪心算法给出的 \(K\) 个消防站，他们之间的距离都会不小于 \(R_{greedy}\)，因为每次都是在距离当前消防站最远的节点建造。在全部建完之后最远距离为 \(R_{greedy}\)，在此之前都不会小于它

• 如果任何两个消防站之间的距离小于 \(2R_{opt}\)，那说明现在已经可以了
• 如果 \(R_{greedy} > 2R_{opt}\)，那么任选两个贪心解法中的消防站 \(a,b\) 和一个最优解中的消防站 \(s_{opt}\) 有 $ dis[a][b] \leq dis[a][s_{opt}] + dis[s_{opt}][b] \leq 2R_{opt} < R_{greedy}$，矛盾

动态规划

HW8Q2 高楼丢鸡蛋

经典 Google 面试题，给定 \(n\) 层楼和 \(m\) 个鸡蛋，定义 \(f(n, m)\) 为最坏情况下确定鸡蛋摔不碎的最少尝试次数，求 \(f(n, m)\)

在 HW7 中将状态直接设置为 \(f(n,m)\)，但是可以考虑间接地做这个题，将状态设置为 \(M(x,m)\) 表示 \(m\) 个鸡蛋在 \(x\) 次尝试下能确定的最高楼层数，则转移方程为

\[M(x, m) = M(x-1, m-1) + M(x-1, m) + 1 \]

这样考虑: 对于 $ M(x, m)$，在 \(M(x-1, m-1)+1\) 层丢一次鸡蛋

• 如果碎了，那么剩下的 \(m-1\) 个鸡蛋可以确定 \(M(x-1, m-1)\) 层，还要加上这一次(因为如果下面的层全部没碎，那么肯定是更高层，而这一层碎了那就对应测试的这一层)
• 如果没碎，那么剩下的 \(m\) 个鸡蛋可以确定 \(M(x-1, m)\) 层

HW8Q5 树上带权最大独立集

树形 DP，算法没什么好说的，主要是看 Python 写算法的代码示例

def max_independent_set(adjacency_list, weights):
    """
    Return a list containing the vertices in the maximum weighted independent set.

    args:
        adjacency_list:ListList[[int]] = the adjacency list of the tree. 
        weights:List[int] = a list of vertex weights. weights[i] is the weight of vertex i.

    return:
        List[int] Containing the labels of the vertices in the maximum weighted independent set.
    """
    n = len(adjacency_list)
    if n == 0:
        return []
    
    # helper function 
    def get_post(adj_list):
        time, post, visited = 1, [0] * n, [False] * n
        unvisited = lambda i: not visited[i]

        def explore(u):
            nonlocal time
            visited[u] = True
            time += 1
            for v in adj_list[u]:
                if unvisited(v):
                    explore(v)
            post[u] = time
            time += 1

        for u in range(n):
            if unvisited(u):
                explore(u)
        return post
    
    post = get_post(adjacency_list)

    def get_children(u):
        yield from filter(lambda v: post[v] < post[u], adjacency_list[u])

    def get_grandchildren(u):
        for v in get_children(u):
            yield from get_children(v)

    dp = [None] * n

    def independent_set_helper(u):
        if dp[u] is not None:
            return dp[u]
        # the first element of the tuple is the weight of the set, the second element is whether the set includes u
        include_self = (weights[u] + sum(independent_set_helper(v)[0] for v in get_grandchildren(u)), True)
        exclude_self = (sum(independent_set_helper(v)[0] for v in get_children(u)), False)
        dp[u] = max(include_self, exclude_self)
        return dp[u]
    
    root = 0
    independent_set_helper(root)

    # get the set of vertices in the maximum weighted independent set
    independent_set = []
    to_check = [root]
    while to_check:
        u = to_check.pop()
        if dp[u][1]:
            independent_set.append(u)
            to_check.extend(get_grandchildren(u))
        else:
            to_check.extend(get_children(u))
    return independent_set

HW8Q5 旅行商问题 TSP

同样是一个看 Python 的题，注意要用 frozenset 作为 key，因为 set 是可变的，不能作为 key

不得不说 Python 还是方便，甚至可以直接写集合差集

def tsp_dp(dist_arr):
    """Compute the exact solution to the TSP using dynamic programming and returns the optimal path.

    Args:
        dist_arr (ndarray[int]]): An n x n matrix of distances between cities. dist_arr[i][j] is the distance from city i to city j.

    Returns:
        List[int]: A list of city indices representing the optimal path.
    """
    n = len(dist_arr)
    if n == 0:
        return []
    dp = {}
    prev = {}
    root = 0

    def tsp_helper(S, i):
        """
        Args:
            S (frozenset[int]): A frozenset of cities that have not been visited.
            i (int): The current city.
        """
        if (S, i) in dp:
            return dp[(S, i)]
        if not S:
            return dist_arr[i][0] # Return to the starting city
        
        min_cost = float('inf')
        prev_city = None
        for city in S:
            cost = dist_arr[i][city] + tsp_helper(S - {city}, city)
            if cost < min_cost:
                min_cost = cost
                prev_city = city
        dp[(S, i)] = min_cost
        prev[(S, i)] = prev_city
        return min_cost
    
    best_cost = tsp_helper(frozenset(range(1, n)), root)
    now_city = root
    tour = [now_city]
    S = frozenset(range(1, n))
    while S:
        now_city = prev[(S, now_city)]
        tour.append(now_city)
        S -= {now_city}
    return tour

线性规划

定义

线性规划是一种优化问题，标准形式如下

maximize \(c^T x\)
subject to \(Ax \leq b\), \(x \geq 0\)

其中 \(A\) 是 \(m \times n\) 的矩阵，\(b\) 是 \(m\) 维向量，\(c\) 是 \(n\) 维向量，\(x\) 是 \(n\) 维向量

对于以下非标准形式，容易将其转化为标准形式:

• 求最小值: 将目标函数取负
• 约束条件为 \(Ax \geq b\): 转化为 \(-Ax \leq -b\)
• 约束条件为 \(Ax = b\): 转化为 \(Ax \leq b\) 和 \(-Ax \leq -b\) (一个大于等于一个小于等于)
• 约束条件为 $ x \leq 0$: 令 \(x = -z\)，转化为 \(z \geq 0\)
• 对 \(x\) 没有约束: 令 \(x = x^+ - x^-\)，转化为 \(x^+, x^- \geq 0\)

对偶形式

canonical LP 的 dual 如下

minimize \(y^T b\)
subject to \(y^T A \geq c^T\), \(y \geq 0\)

• 弱对偶: 对于任意可行解 \(x\) 和 \(y\)，有 \(c^T x \leq y^T b\)
• 强对偶: 最优解 \(x^*\) 和 \(y^*\) 满足 \(c^T x^* = y^{*T} b\)

单纯形法

1. 从任意顶点开始，将其表示为 \(x\)
2. 考虑 \(x\) 的所有邻居 \(y\)
3. 如果 \(y\) 比 \(x\) 更优，那么令 \(x = y\)，重复步骤 2
4. 如果 \(x\) 没有更优的邻居，那么 \(x\) 就是最优解

这里邻居的定义是: \(x\) 和 \(y\) 有且仅有一个限制条件不同(因为顶点都可以表示为 \(m\) 个限制条件的交集)

零和游戏(Zero-Sum Game) (todo)

网络流

定义

• 一个网络可以表示为 \((G, c, s, t)\)，其中 \(G = (V, E)\) 是一个有向图，\(c: E \rightarrow \mathbb{R}^+\) 是容量函数，\(s, t \in V\) 分别是源和汇
• 一个流是一个函数 \(f: V \times V \rightarrow \mathbb{R}\)，满足以下三个性质
  • 容量限制: 对于所有 \(u, v \in V\)，有 \(0 \leq f(u, v) \leq c(u, v)\)
  • 反对称性: 对于所有 \(u, v \in V\)，有 \(f(u, v) = -f(v, u)\)
  • 流守恒: 对于所有 \(u \in V - \{s, t\}\)，有 $ \displaystyle\sum_{v \in V} f(u, v) = 0$
• 残留网络: 给定一个网络 \((G, c, s, t)\) 和一个流 \(f\)，那么残留网络 \(G_f = (V, E_f)\) 定义为 \(E_f = \{(u, v) \in V \times V | c_f(u, v) > 0\}\)，其中 \(c_f(u, v) = c(u, v) - f(u, v)\)，这实际上就是排除那些 \(c_f(u, v) = 0\) 的边

Ford-Fulkerson 算法

不断地在残留网络中找一条增广路径(augmenting path)，然后增广，直到不存在增广路径为止

时间复杂度为 \(O(mF)\)，其中 \(F\) 是最大流的大小，因为每次增广都会增加至少 1，而每次增广的时间复杂度为 \(O(m)\)

不过这个算法定义并不精确，因为找一条增广路的方法可能有多种：通过 DFS、A* 搜索、通过一些需要 几百个 RTX A6000 来训练的 RL 模型，或者通过魔法......

正确性

正确性在于这个算法找到了一个原图的割，而最大流等于最小割，考虑最终的残留网络中源点可以访问到的点和不能访问到的点所构成的割即可

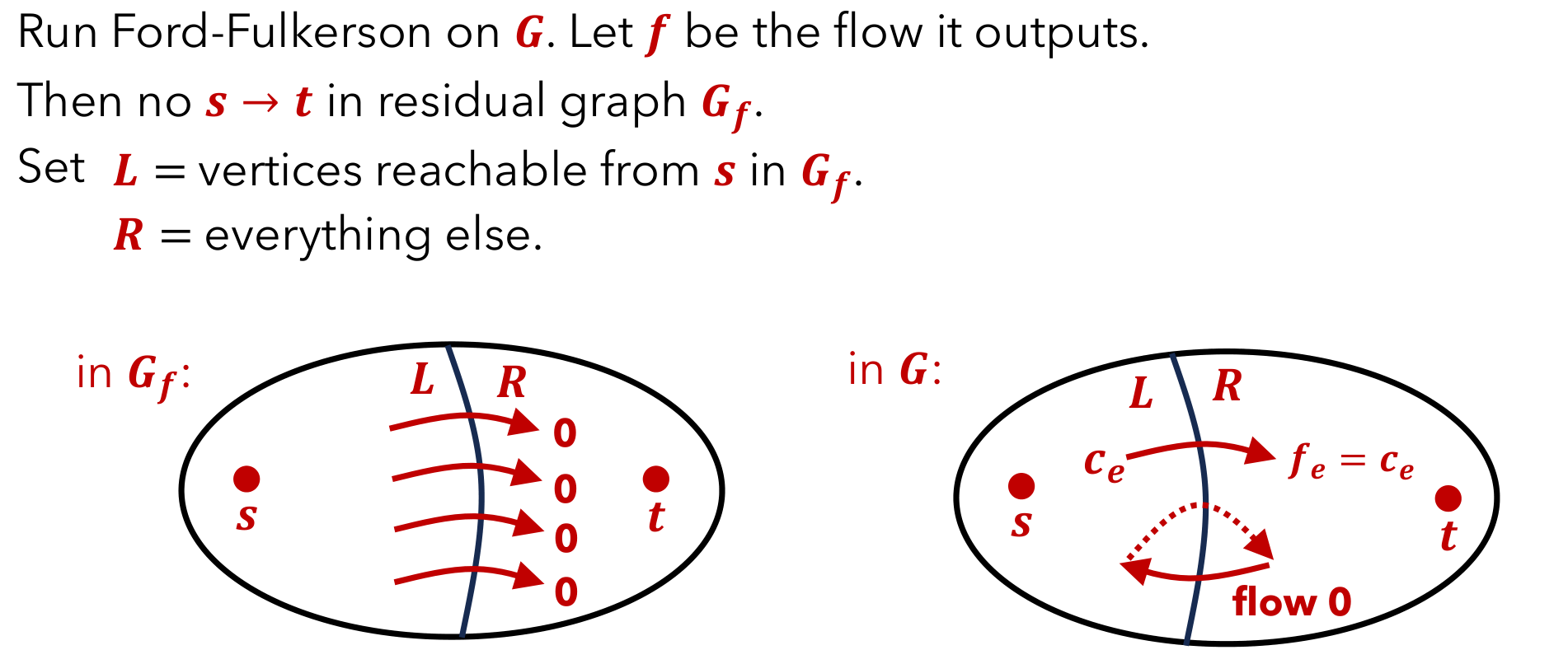
HW9Q5 残量图

问题描述

给定一个网络 \((G, c, s, t)\) 和一个被找到的最大流 \(f\)(均为整数)
现在有一条 \(f_e = c_e\) 的边 \(e=(u,v)\) (就是在最大流中被用满了的边)，将其容量减小 \(1\)，得到一个新的网络 \((G, c', s, t)\)，求新网络的最大流，要求时间复杂度为 \(O(|V| + |E|)\)

解法与正确性证明

首先我们可以根据原网络和最大流构造出原残留网络，然后我们考虑怎么修改

核心思想就是退流

• 先考虑能不能直接退，也就是尝试在原残留网络中找一条从 \(v\) 到 \(u\) 的路径，如果能找到，那么就说明有一个包含 \(u\) 和 \(v\) 的圈，直接都减一即可
• 找不到的话就找从 \(s\) 到 \(u\) 的路径和从 \(v\) 到 \(t\) 的路径，这一定能找到，不然这条边上根本不会有流经过，然后将这两条路径合并，就得到了一条从 \(s\) 到 \(t\) 的路径，这样就可以退流了

退流之后再跑一遍 Ford-Fulkerson 算法就可以了，因为最大流变化不超过 \(1\)，所以时间复杂度为 \(O(|V| + |E|)\)

HW9Q9 Edmonds-Karp 算法

如果用 BFS 找增广路，复杂度降为 \(O(m^2 n)\) 其中 \(n\) 是节点数， \(m\) 是边数，代码如下

def bfs_augmenting_path(g, s, t):
    """
    args:
        g:nx.DiGraph = directed network flow graph
        s:int = source node s
        t:int = sink node t
    return:
        List[int] representing the augmenting path that BFS finds. First 
            and last nodes should be s and t respectively. Return [] if 
            path doesn't exist. Ex: [s, a, b, t] if (s, a), (a, b), (b, t)
            is the shortest length augmenting path.
    """
    queue = deque([(s, [s])])
    visited = set()
    while queue:
        node, path = queue.popleft()
        if node == t:
            return path
        if node in visited:
            continue
        visited.add(node)
        for neighbor in g.neighbors(node):
            if g.edges[node, neighbor]["capacity"] > g.edges[node, neighbor]["flow"]:
                queue.append((neighbor, path + [neighbor]))
    return []


def edmonds_karp(g, s, t):
    """
    args:
        g:nx.DiGraph = directed network flow graph
        s:int = source node s
        t:int = sink node t
    return:
        Tuple(int, nx.DiGraph) where the first value represents the max flow that
            was successfully pushed, and the second value represents the graph
            where the flow values along each edge represents the flow pushed through
            that edge.
    """
    graph = nx.algorithms.flow.build_residual_network(g.copy(), "capacity")
    nx.set_edge_attributes(graph, 0, "flow")
    flow = 0
    
    def augment(g, path):
        flow = float("inf")
        for i in range(len(path) - 1):
            e = g.edges[path[i], path[i + 1]]
            flow = min(flow, e["capacity"] - e["flow"])
        for i in range(len(path) - 1):
            e_forward = g.edges[path[i], path[i + 1]]
            e_backward = g.edges[path[i + 1], path[i]]
            e_forward["flow"] += flow
            e_backward["flow"] -= flow
        return flow
    
    # Use the augment function to compute the max flow
    path = bfs_augmenting_path(graph, s, t)
    while path:
        flow += augment(graph, path)
        path = bfs_augmenting_path(graph, s, t)
    return flow, graph

然后可以直接找到最小割，代码如下

def find_min_cut(g, s, t):
    """
    args:
        g:nx.DiGraph = directed network flow graph
        s:int = source node s
        t:int = sink node t
    return:
        Set(int) that contains all vertices in the min cut of g that includes s.
    """
    vertex_cut_s = set([s])
    flow, graph = edmonds_karp(g, s, t)
    q = deque([s])
    while q:
        u = q.popleft()
        for v in graph.neighbors(u):
            if v not in vertex_cut_s and graph.edges[u, v]["capacity"] > graph.edges[u, v]["flow"]:
                vertex_cut_s.add(v)
                q.append(v)
    return vertex_cut_s

P 与 NP

规约(reduction)

一个例子是 3-SAT 问题到独立集问题的规约，记作 \(3-SAT \leq_p IndependentSet\)

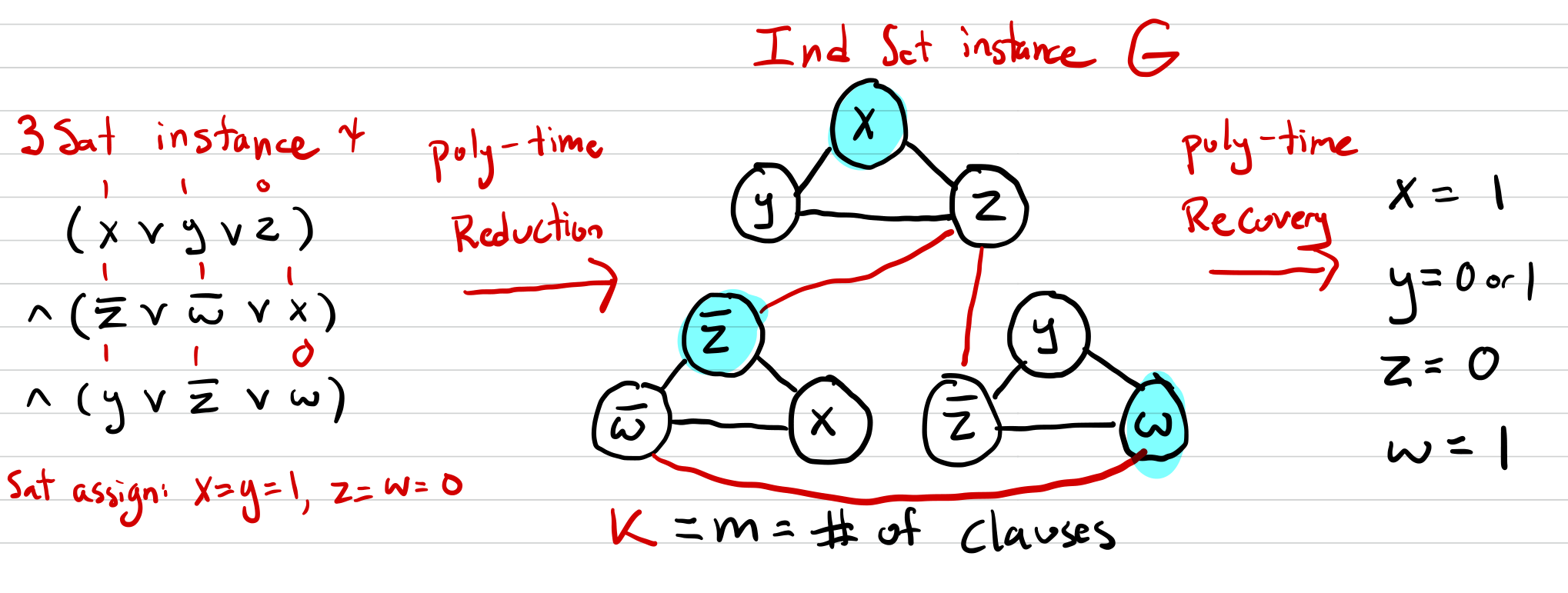
加边如上图所示

• 假设存在一个 3-SAT 的赋值，对于每一个字句，取出某一个令其为真的即可，其他的两个不要
• 假设存在一个独立集，那么对于每一个字句，取出一个在独立集中的点即可

HW10Q6 Decision vs. Search vs. Optimization

考虑点覆盖问题，以下是三个版本:

• Decision(决策): 给定一个图 \(G\) 和一个整数 \(k\)，判断是否存在一个点覆盖大小不超过 \(k\)，如果存在则输出 TRUE，否则输出 FALSE
• Search(搜索): 给定一个图 \(G\)，找到一个大小不超过 \(k\) 的点覆盖
• Optimization(优化): 给定一个图 \(G\)，找到一个大小最小的点覆盖

乍一看好像优化比搜索更难，搜索又比决策更难，但是实际上他们一样难

从搜索到优化只需要加一个二分即可

从决策到搜索，考虑以下过程
假如给定一个图 \(G\) 和一个整数 \(k\)，我们先运行 Decision\((G, k)\)，如果返回 FALSE，否则循环运行以下过程直到边都被删完

1. 任选顶点 \(v \in G\)，删除 \(v\) 和 \(v\) 的所有边
2. 运行 Decision\((G\backslash \{v\}, k-1)\)
   • 如果返回 FALSE，那么撤销上一步操作，把 \(v\) 和 \(v\) 的所有边加回来
   • 如果返回 TRUE，那么 \(k\) 减一，继续循环

Disc12Q3 Cycle Cover

给定一个有向图 \(G\)，判断能否用几个互不重叠的环将其覆盖。要求将其规约到完美二分匹配问题

建模比较简单(虽然没完全做出来)，对每个 \(G\) 中的顶点 \(v\)，建立两个顶点 \(v_L, v_R\)，然后对于每条边 \((u, v)\)，建立一条从 \(u_L\) 到 \(v_R\) 的边，然后求完美二分匹配即可。如果有完美匹配，这里就会形成若干个类似循环群的东西，然后每个循环群就是一个环

HW12Q3 3-SAT to 3-Coloring

给定一个 3-SAT 公式，判断是否存在一个赋值使得公式为真，要求将其规约到 3-Coloring 问题

1. 从三个特殊顶点开始，标记为 \(v_{BASE}, v_{TRUE}, v_{FALSE}\)，然后有边 \((v_{BASE}, v_{TRUE})\) 和 \((v_{BASE}, v_{FALSE})\) 还有 \((v_{TRUE}, v_{FALSE})\)

2. 然后对于每个文字 \(x_i\)，建立两个顶点 \(x_i, \neg x_i\)，连边 \((x_i, \neg x_i)\) 和 \((x_i, v_{BASE})\) 和 \((\neg x_i, v_{BASE})\)，这样就保证 \(x_i\) 和 \(\neg x_i\) 分别和 \(v_{TRUE}\) 和 \(v_{FALSE}\) 同色

3. 利用下图的小工具

   

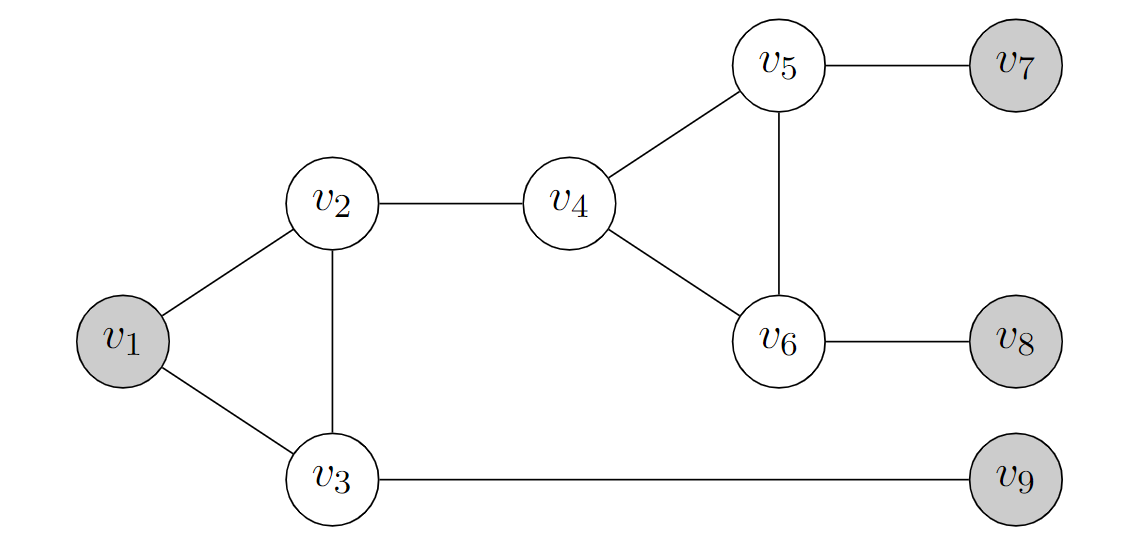
   注意如果灰色节点都只能分配某两种颜色(其实就是 \(v_{TRUE}\) 和 \(v_{FALSE}\) 对应的颜色，假定为蓝色和绿色)的话，那么如果 \(v_1\) 是绿色，那么剩下的右边三个灰色节点必然至少有一个是绿色(可以暴力证明)

   这直接对应了 3-SAT 中的子句

4. 对于每个字句，设置一个对应的 \(v_1\)(设为 \(C_j\) )使其为真。具体地说，连接 \((C_j， v_{FALSE})\) 和 \((C_j, v_{BASE})\)，然后对涉及的三个变量构建小工具即可

HW12Q6 正交向量

正交向量问题: 给定两个向量集合 \(A,B\)，所有向量都属于 \(\{0, 1\}^m\)，且 \(|A| = |B| = n\)，要求从 \(A\) 中选一个向量 \(a\)，从 \(B\) 中选一个向量 \(b\)，使得 \(a \cdot b = 0\)，求是否存在这样的 \(a, b\)。这个问题显然有一个暴力的 \(O(n^2 m)\) 的算法

我们试图证明这个问题不太可能有一个 \(O(n^{2-\epsilon} m)\) 的算法，其中 \(\epsilon > 0\)，利用强指数时间假说(Strong Exponential Time Hypothesis, SETH)，即 3-SAT 问题不存在一个 \(O(2^{n-\epsilon} m)\) 的算法，其中 \(\epsilon > 0\)

为了方便，假设 3-SAT 问题中的变量为偶数个

将其分为两部分 \(V_1, V_2\)，每个部分有 \(n/2\) 个变量。对于 \(V_1\)，枚举 \(V_1\) 中变量所有的赋值情况，共有 \(2^{n/2}\) 种，对于每种赋值情况，将其转化为一个向量，具体规则是如果这种赋值规则在不考虑 \(V_2\) 中变量的情况下(因为是或的关系) 就可以令第 \(i\) 个子句为真，那么就将这个向量的第 \(i\) 位设为 \(0\)，否则设为 \(1\)，这样就得到了 \(2^{n/2}\) 个向量，记为 \(A\)，同理得到 \(B\)，然后就可以用上面的算法了