基于拓扑结构检测的LDPC稀疏校验矩阵高阶环检测算法matlab仿真

1.引言

LDPC（低密度奇偶校验）码作为一种性能卓越的信道编码技术，其校验矩阵的结构对解码性能有着至关重要的影响。其中，矩阵中存在的环（Cycle），尤其是短环，会使解码过程中的消息传递产生相关性，进而降低码的纠错能力。

2.算法仿真效果演示

3.数据集格式或算法参数简介

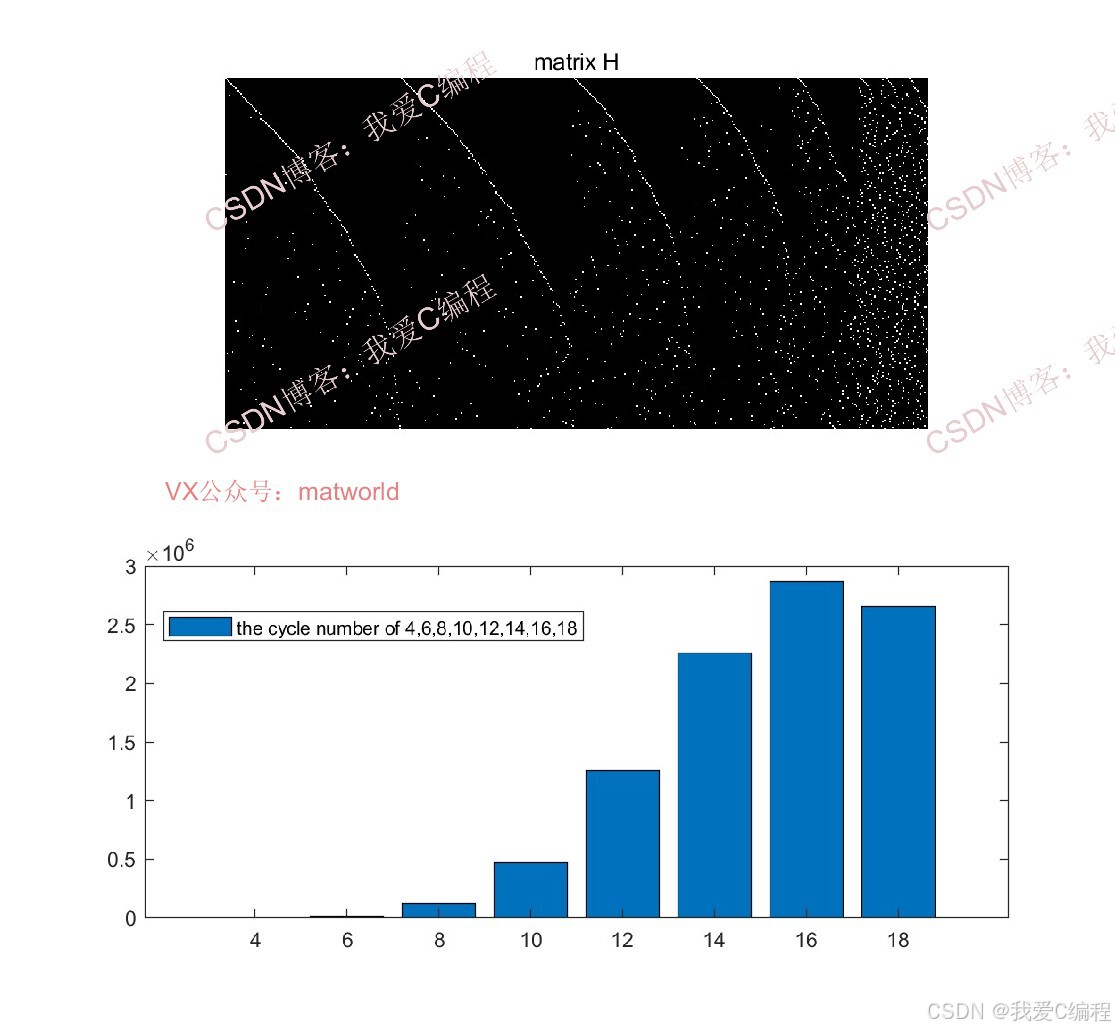
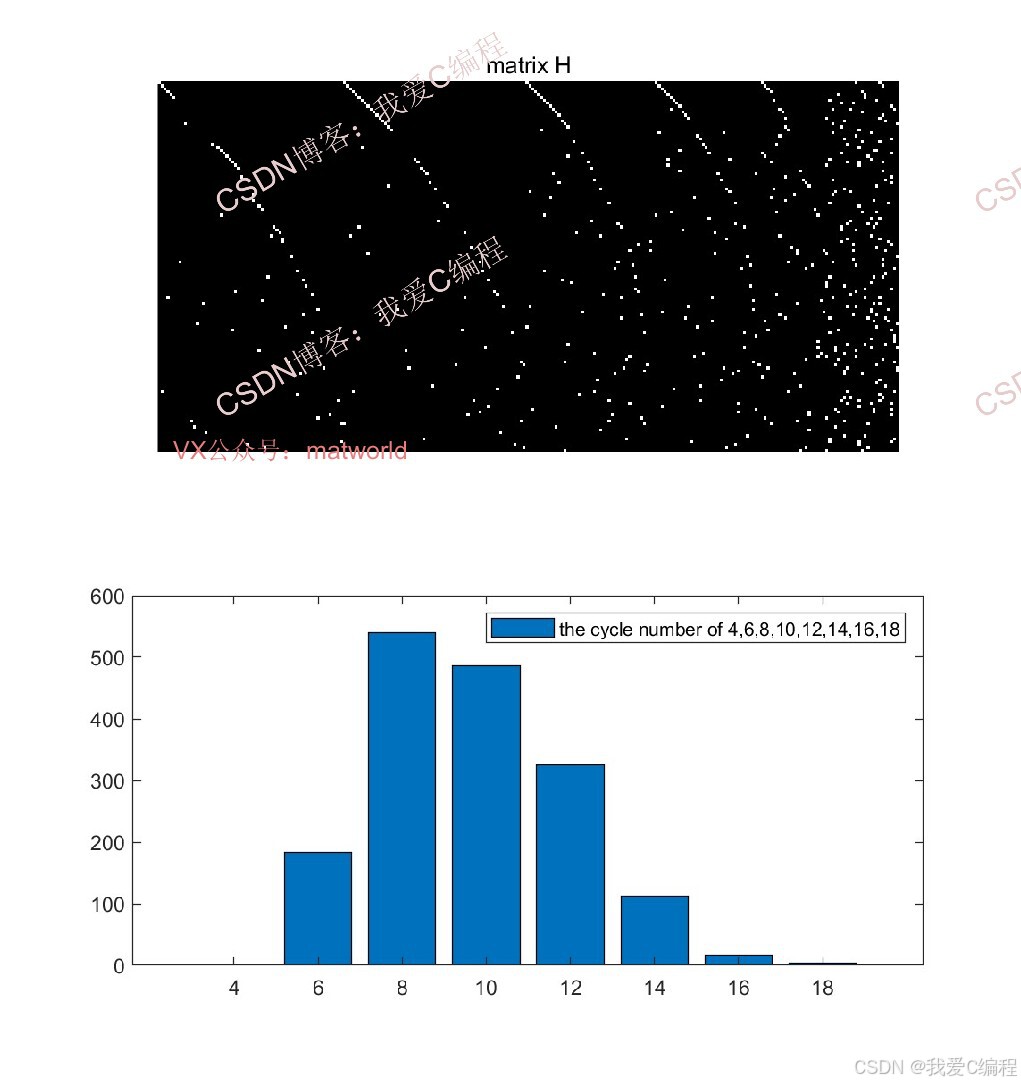
H矩阵分别采用252*504和126*252两种大小的校验矩阵

4.算法涉及理论知识概要

LDPC 码的校验矩阵H可以用二分图表示，该图由两类节点构成：

变量节点（Variable Nodes）：对应信息位和校验位，用圆形表示。

校验节点（Check Nodes）：对应校验方程，用方形表示。

当且仅当Hi,j​=1时，变量节点j与校验节点i之间存在一条边。

随着环长度k的增加，计算复杂度呈指数级增长。实际应用中，通常只检测到8环或10环。在本课程中，我们增加到18环，但仿真时间会大于15小时。如果电脑配置低，可以降低到10环。

LDPC码校验矩阵的环结构分析是码设计中的关键环节。高阶环检测算法通过图论和矩阵理论，帮助工程师评估和优化码的结构。虽然计算复杂度较高，但通过算法优化和并行计算，可在实际应用中实现高效检测。