m基于ACO蚁群优化的FCM模糊聚类算法matlab仿真

1.算法概述

       蚁群算法是通过对自然界中真实蚂蚁的集体行为的观察,模拟而得到一种仿生优化算法,它具有很好的并行性,分布性.根据蚂蚁群体不同的集体行为特征,蚁群算法可分为受蚂蚁觅食行为启发的模型和受孵化分类启发的模型,受劳动分工和协作运输启发的模型.本文重点研究了前两种蚁群算法模型. 受蚂蚁觅食行为启发的模型又称为蚁群优化算法(ACO),是继模拟退火算法,遗传算法,禁忌搜索等之后又一启发式智能优化算法.目前它已成功应用于求解TSP问题,地图着色,路径车辆调度等优化问题.本文针对蚁群算法收敛时间长,易陷入局部最优的缺点,通过对路径上信息素的更新方式作出动态调整,建立信息素平滑机制,进而使得不同路径上的信息素的更新速度有所不同,从而使改进后算法能够有效地缩短搜索的时间,并能对最终解进行优化,避免过早的陷入局部最优. 聚类是数据挖掘的重要技术之一,它可按照某种规则将数据对象划分为多个类或簇,使同一类的数据对象有较高的相似度,而不同类的数据对象差异较大.       

 

       用FCM算法实现基于目标函数的模糊聚类又称交替的迭代优化法。迭代优化本质上属于局部搜索的爬山法，很容易陷入局部极值点，因此对初始化很敏感。通常是根据一定的经验准则选取初始参数，这样计算结果与初始参数设置是否恰当密切相关。特别是在数据量较大和高维情况下，设置合理的参数非常困难，只能通过多次实验比较选定。由于初始聚类中心和样本的输入次序对最终的结果有重大影响，往往是用若干不同的初始中心和聚类数目分别聚类，然后选择最满意的聚类作为最终的结果。 通过蚁群算法，我们可以得到最佳的初始聚类中心，然后进行快速的聚类。

 

2.仿真效果预览

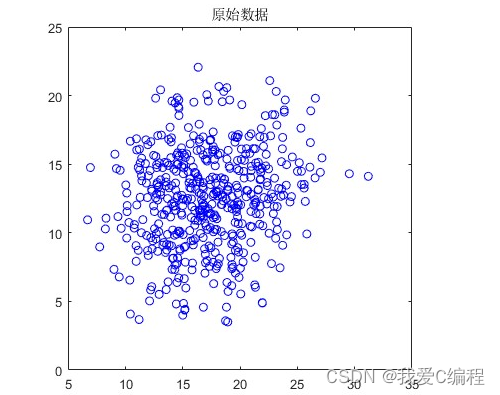
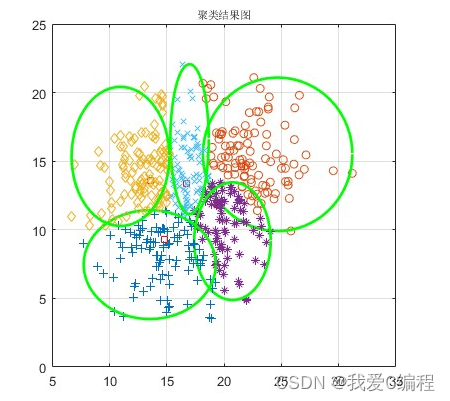
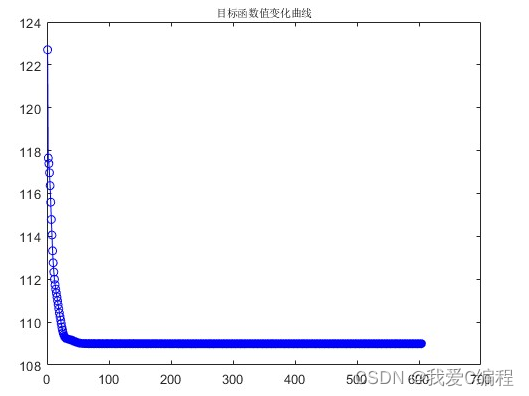
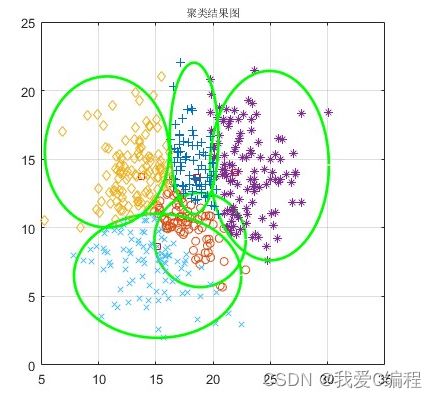
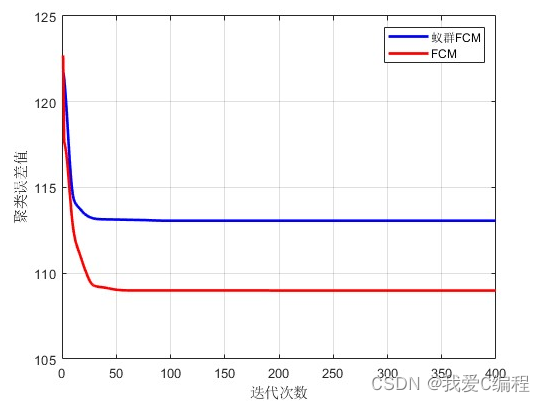
matlab2022a仿真结果如下：

 

 

 

 

 

3.核心MATLAB程序

 

function cluster_center = func_ant_opt(data,Class_Num);
 
X     = data;
%N =测试样本数;n =测试样本的属性数;
[N,n] = size(X); 
%K = 组数; 
K     = Class_Num; 
%R = 蚂蚁数; 
R     = 200;      
%t_max =最大迭代次数;  
t_max = 100;               
% 初始化
c     = 10^-1;
tau   = ones(N,K) * c;    %信息素矩阵，初始值为0.001的N*K矩阵（样本数*聚类数）
q     = 0.90;                % 阈值q
rho   = 0.1;              % 蒸发率
best_solution_function_value = inf; % 最佳路径度量值（初值为无穷大，该值越小聚类效果越好）
tic                     %计算程序运行时间
t = 1; 
 
%=======程序终止条件（下列两个终止条件任选其一）======
 while ((t<=t_max))                             %达到最大迭代次数而终止
%========================= 
    %路径标识字符：标识每只蚂蚁的路径
    solution_string = zeros(R,N+1);     
    for i = 1 : R                       %以信息素为依据确定蚂蚁的路径
        r = rand(1,N);    %随机产生值为0-1随机数的1*51的数组
        for g = 1 : N
            if r(g) < q     %如果r(g)小于阈值
                tau_max = max(tau(g,:));
                Cluster_number = find(tau(g,:)==tau_max);   %聚类标识数，选择信息素最多的路径
                solution_string(i,g) = Cluster_number(1);   %确定第i只蚂蚁对第g个样本的路径标识
            else            %如果r(g)大于阈值,求出各路径信息素占在总信息素的比例，按概率选择路径
                sum_p = sum(tau(g,:)); 
                p = tau(g,:) / sum_p; 
                for u = 2 : K 
                    p(u) = p(u) + p(u-1); 
                end
               rr = rand;          
                for s = 1 : K 
                    if (rr <= p(s)) 
                       Cluster_number = s;
                       solution_string(i,g) = Cluster_number;  
                    break; 
                end 
            end
        end
    end
 
    % 计算聚类中心
    weight = zeros(N,K);
       for h = 1:N              %给路径做计算标识
           Cluster_index = solution_string(i,h); %类的索引编号          
           weight(h,Cluster_index) = 1;          %对样本选择的类在weight数组的相应位置标1
       end
 
       cluster_center = zeros(K,n);  %聚类中心（聚类数K个中心）
       for j = 1:K
           for v = 1:n
               sum_wx = sum(weight(:,j).*X(:,v));   %各类样本各属性值之和
               sum_w = sum(weight(:,j));            %各类样本个数
               if sum_w==0                          %该类样本数为0，则该类的聚类中心为0
                 cluster_center(j,v) =0
                  continue;
               else                                 %该类样本数不为0，则聚类中心的值取样本属性值的平均值
               cluster_center(j,v) = sum_wx/sum_w;
               end
            end
       end
 
    % 计算各样本点各属性到其对应的聚类中心的均方差之和，该值存入solution_string的最后一位
      F = 0;
      for j= 1:K
          for ii = 1:N
              Temp=0;
              if solution_string(i,ii)==j;                
                  for v = 1:n
                      Temp = ((abs(X(ii,v)-cluster_center(j,v))).^2)+Temp;
                  end
                  Temp = sqrt(Temp);
              end
            F = (Temp)+F;
          end        
      end
 
       solution_string(i,end) = F;                      
 
    end 
    %根据F值，把solution_string矩阵升序排序
    [fitness_ascend,solution_index] = sort(solution_string(:,end),1);
    solution_ascend = [solution_string(solution_index,1:end-1) fitness_ascend];
 
    pls = 0.1;        %局部寻优阈值pls（相当于变异率）
    L = 2;              % 在L条路径内局部寻优
    % 局部寻优程序
    solution_temp = zeros(L,N+1);
    k = 1;
    while(k <= L)
           solution_temp(k,:) = solution_ascend(k,:);
           rp = rand(1,N);     %产生一个1*N(51)维的随机数组，某值小于pls则随机改变其对应的路径标识
           for i = 1:N
               if rp(i) <= pls
                   current_cluster_number = setdiff([1:K],solution_temp(k,i));
                   rrr=1+floor((K-2)*rand(1,1));
                   change_cluster = current_cluster_number(rrr);
                   solution_temp(k,i) = change_cluster;
               end
           end
 
        % 计算临时聚类中心   
           solution_temp_weight = zeros(N,K);
           for h = 1:N
               solution_temp_cluster_index = solution_temp(k,h);           
               solution_temp_weight(h,solution_temp_cluster_index) = 1;
           end
 
           solution_temp_cluster_center = zeros(K,n);
           for j = 1:K
               for v = 1:n
                   solution_temp_sum_wx = sum(solution_temp_weight(:,j).*X(:,v));
                   solution_temp_sum_w = sum(solution_temp_weight(:,j));
                   if solution_temp_sum_w==0
                   solution_temp_cluster_center(j,v) =0;
                   continue;
                   else
                       solution_temp_cluster_center(j,v) = solution_temp_sum_wx/solution_temp_sum_w;
                   end
               end
          end
          % 计算各样本点各属性到其对应的临时聚类中心的均方差之和Ft；
          solution_temp_F = 0;
          for j= 1:K
              for ii = 1:N
                  st_Temp=0;
                  if solution_temp(k,ii)==j;                               
                      for v = 1:n
                          st_Temp = ((abs(X(ii,v)-solution_temp_cluster_center(j,v))).^2)+st_Temp;
                      end
                      st_Temp = sqrt(st_Temp);
                  end
                  solution_temp_F = (st_Temp)+solution_temp_F;
              end
          end
        solution_temp(k,end) = solution_temp_F;   
        %根据临时聚类度量调整路径
        % 如果 Ft<Fl 则 Fl=Ft ， Sl=St
          if solution_temp(k,end) <= solution_ascend(k,end)              
              solution_ascend(k,:) = solution_temp(k,:);               
          end
 
          if solution_ascend(k,end)<=best_solution_function_value
              best_solution = solution_ascend(k,:);
          end
      k = k+1;
      end   
 
    % 用最好的L条路径更新信息数矩阵
    tau_F = 0;
    for j = 1:L    
       tau_F = tau_F + solution_ascend(j,end);
    end
    for i = 1 : N        
       tau(i,best_solution(1,i)) = (1 - rho) * tau(i,best_solution(1,i)) + 1/ tau_F; 
    %1/tau_F和rho/tau_F效果都很好
    end 
    t=t+1
    best_solution_function_value =  solution_ascend(1,end);
end
02-011M