m基于ACO蚁群算法的考虑装载率的循环送货的最短线路规划MATLAB仿真
1.算法概述
根据这些装载率再结合路径最短来设计几个循环送货的线路。最理想状态是一条循环路径出去把所有的货都能遍历,并且装载率也很高。但是显然理想状态不可能,所以我们要做的就是尽量往理想状态靠,通过这些数据,用最少的循环路径条数(或者说最经济的)和最高的装载率以及最少的每条路径遍历次数(这些加起来基本就能看做是最低成本),来把那些货运完。
根据你所提供的参数资料,目前,我们所需要考虑的影响成本的几个因素为:
·每辆卡车的装货量;
·每个地点的坐标值;
·每个地点的频数,货物种类以及数量,体积;
·卡车的耗油量;
这里由于原先考虑出现点问题,这里考虑每辆卡车的优化方案分别进行仿真分析。
这里所设计的环路方案,必须满足如下的几个条件:
第一:每个点通过次数必须满足规定的频次;
第二:从原点出发,在装载率最大化的情况下尽可能多的历遍点,然后返回节点;
第三:在完成所有节点的频次需求和货物需求所需要的路线最短即油耗最小。
通过上面的分析,整个问题即,卡车每次装多少种类的多少数目的货物出发送货(装载量),且完成送货任务总路径最短,中间可能回来取货(油耗),每个点通过次数在规定次数之内,此时的成本最低。并且,每次送货的装载量又决定了最终的路线长度即油耗,这里省略掉时间成本。这里单独考虑每辆卡车的优化任务。
通过上面的分析可知,这里的优化问题,本质上是一个VRP和VFP的联合问题,即车辆调度循环发送和装载的联合问题。
这里,我们的优化目标函数为:
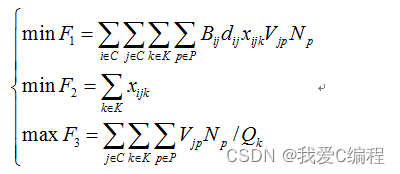
这里的函数含义是:
成本最低;
路径综合最短;
每条线路的装载率最大;


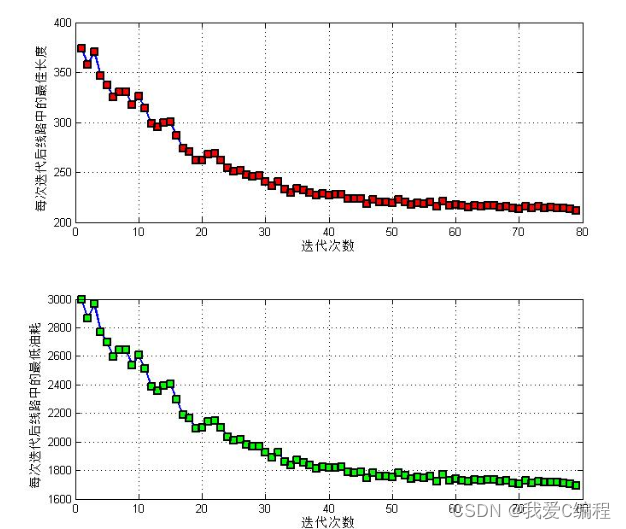
2.仿真效果预览
matlab2022a仿真结果如下:
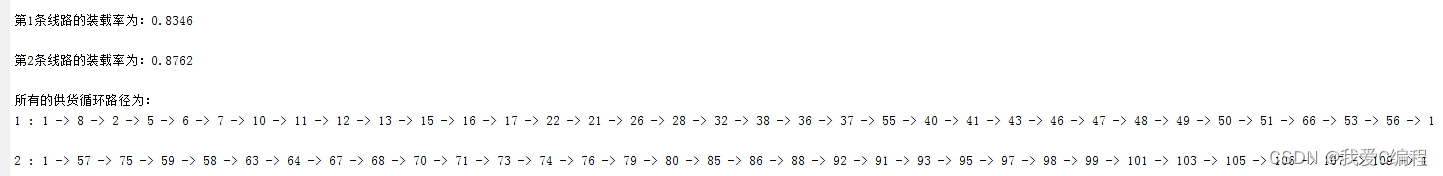
3.核心MATLAB程序
.................................................................
%映射表
B = func_maps(C_f);
%计算规模和权值的初始值
[SCALEs,Wsd]=func_w(C);
%中心和每个供货点之间连接能节省的距离
Save_d = func_save_d(SCALEs,Wsd);
LOADs = 0;
Eer = 1./Wsd; %启发常系数
Tau = ones(SCALEs,SCALEs);
Save_roads = zeros(Num_ann,SCALEs+20);%生成路的径
Iteration = 1;
Best_roads = [Iter,SCALEs+20]; %各代最佳路线
Best_roads_Lens = inf.*ones(Iter,1); %各代最佳路线的长度
Best_roads_Lens_avgs = zeros(Iter,1); %各代路线的平均长度
flag = 0;
%进行蚁群+PSO算法
while (Iteration <= Iter)
disp('当前迭代次数')
Iteration
%产生随机变量作为初始化粒子
Save_roads(:,1) = randint(Num_ann,1,[1,1]);
flag = zeros(SCALEs,1);
%按如下的规则进行循环历遍
pp = 0;
for i=1:Num_ann
pp = 0;
%指定随机性
% RandStream.setDefaultStream(RandStream('mt19937ar','seed',Iteration*i));
Will_walks = Save_roads(i,:);
Will_walks = Will_walks(Will_walks>0);
Will_walks2 = setdiff(1:SCALEs,Will_walks);
c_temp = length(Will_walks2);
Jer=1;
while Jer <= SCALEs
pp = pp +1;
if isempty(Will_walks2) == 0
%按照规则选下一个供货点或者是回到中心
for k=1:length(Will_walks2)
x(k) = (Tau(Will_walks(end),Will_walks2(k))) *...
(Eer(Will_walks(end),Will_walks2(k))) *...
(Save_d(Will_walks(end),Will_walks2(k))^2);
end
Pers = rand(1,1);
if Pers < 0.1
choices = find(max(x));
else
x = x/(sum(x));
xcum = cumsum(x);
choices = find(xcum>=rand(1,1));
end
%以下是对每个供货点进行供货的装载情况的计算
if isempty(choices) == 1
choices = 1;
%计算当前供货点的物件数量和体积
INDs = choices;
INDs2 = INDs;
LOADs = LOADs + V1{INDs2}(choices);
else
INDs = Will_walks2(choices(1));
%对当前点下的情况进行装货
INDs2 = B(INDs,2);
%计算当前点种的货物的种类
ZL = length(V1{INDs2});
%%产生一组概率进行选择货物,如果装载满足需求,则继续装,否则不装
%NNS = floor(ZL*rand(1,1)) + 1;
NNS = 1;
for NNS = 1:ZL
CC = Nums{INDs2}(NNS);
while CC > 0 & LOADs <= lemda*Qv
Vtmp = V1{INDs2}(NNS);%选择的货物的体积大小
%然后进行装载
LOADs = LOADs + Vtmp;
%存货数量减1
CC = CC-1;
Nums{INDs2}(NNS) = CC;
end
end
end
%计算装载率
if LOADs <= lemda*Qv
WW(i,pp) = LOADs/(lemda*Qv);
end
if LOADs > lemda*Qv%装满则返回
choices = 1;
Jer = Jer-1;
LOADs = 0;
Save_roads(i,length(Will_walks)+1) = choices(1);
else
Save_roads(i,length(Will_walks)+1) = Will_walks2(choices(1));
end
end
Will_walks = Save_roads(i,:);
Will_walks = Will_walks(Will_walks>0);
Will_walks2 = setdiff(1:SCALEs,Will_walks);
x = [];
if Will_walks(end) > 1 | Will_walks(end) < 1
Save_roads(i,1:(length(Will_walks)+1))=[Will_walks,1];
end
if sum(Nums{INDs2}) == 0
flag(Jer) = INDs;
else
flag(Jer) = 0;
end
Jer=Jer+1;
end
LOADs=0;
end
L = zeros(Num_ann,1);
for i=1:Num_ann
tmpsss = Save_roads(i,:);
R = tmpsss(tmpsss>0);
for j=1:(length(R)-1)
L(i) = L(i) + Wsd(R(j),R(j+1));
end
end
Best_roads_Lens(Iteration) = min(L);
pos = find(L==Best_roads_Lens(Iteration));
Best_roads(Iteration,1:length(Save_roads(pos(1),:))) = Save_roads(pos(1),:);
SELS = find(Best_roads(Iteration,:)==1);
Best_save = [];
Best_save2 = 0;
for Si=1:(length(SELS)-1)
YBEST = Best_roads(Iteration,SELS(Si):SELS(Si+1));
al = length(YBEST);
T = zeros((length(SELS)-1),1);
for Sj=1:(al-1)
T(Si)=T(Si)+Wsd(YBEST(Sj),YBEST(Sj+1));
end
for Sp=2:(al-1)
for Sq=(Sp+1):(al-1)
DD = YBEST;
temp1 = DD(Sp);
temp2 = DD(Sq);
DD(Sp) = temp2;
DD(Sq) = temp1;
TT = zeros(1);
for Sj=1:(al-1)
TT = TT + Wsd(DD(Sj),DD(Sj+1));
end
if TT<T(Si)
T(Si) = TT;
YBEST = DD;
end
end
end
if Si>=2
YBEST = YBEST(2:al);
end
Best_save = [Best_save,YBEST];
Best_save2= Best_save2+T(Si);
end
Best_roads_Lens(Iteration) = Best_save2;
Best_roads(Iteration,1:length(Best_save)) = Best_save;
Best_save = [];
Best_save2 = 0;
Best_roads_Lens_avgs(Iteration) = mean(L);
LOADs = 0;
Iteration = Iteration+1;
Delta_Tau=zeros(SCALEs,SCALEs);
for i=1:Num_ann
MM = Save_roads(i,:);
R = MM(MM>0);
for j=1:(length(R)-1)
Delta_Tau(R(j),R(j+1))=Delta_Tau(R(j),R(j+1))+Importance/L(i);
end
end
Tau = (1-Rr).*Tau+Delta_Tau;
%清零
Save_roads = zeros(Num_ann,SCALEs);
end
%优化结果
Pos = find(Best_roads_Lens==min(Best_roads_Lens));
best_route = Best_roads(Pos(1),:);
best_route = best_route(best_route>0);
for i = 1:SCALEs
Load_rate(i) = mean(WW(:,i));
end
%装载率的变化
%装载率的变化
disp('装载率:');
max(Load_rate)
.................................
02-008m


 浙公网安备 33010602011771号
浙公网安备 33010602011771号