最少步数(广搜,剪枝)
最少步数(广搜,剪枝)
描述
在各种棋中,棋子的走法总是一定的,如中国象棋中马走“日”。有一位小学生就想如果马能有两种走法将增加其趣味性,因此,他规定马既能按“日”走,也能如象一样走“田”字。
他的同桌平时喜欢下围棋,知道这件事后觉得很有趣,就想试一试,在一个(100×100)的围棋盘上任选两点A、B,A点放上黑子,B点放上白子,代表两匹马。棋子可以按“日”字走,也可以按“田”字走,俩人一个走黑马,一个走白马。谁用最少的步数走到左上角坐标为(1,1)的点时,谁获胜。现在他请你帮忙,给你A、B两点的坐标,想知道两个位置到(1,1)点可能的最少步数。
格式
输入格式
A、B两点的坐标。
输出格式
最少步数。
样例
输入样例
12 16
18 10
输出样例
8
9
代码:
#include <iostream>
#include <stdio.h>
#include <string>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
int num[][2]={{-2,-2},{-2,-1},{-1,-2},{-2,1},{-2,2},{-1,2},{1,-2},{2,-2},{2,-1},{1,2},{2,1},{2,2}};
bool visit[128][128];
void init()
{
for(int i=0;i<128;++i)
{
for(int j=0;j<128;++j)
{
visit[i][j]=false;
}
}
}
struct ver
{
int row;//行
int col;//列
int step;//步数
};
void BFS(struct ver v)
{
v.step=0;
queue<ver> Myqueue;
visit[v.row][v.col]=true;
Myqueue.push(v);
if(v.row==1&&v.col==1)
{
printf("%d\n", v.step);
return ;
}
if(v.row<0||v.col<0||v.row>100||v.col>100)
{
return ;
}
while(!Myqueue.empty())
{
struct ver now=Myqueue.front();
struct ver temp=now;
Myqueue.pop();
for(int i=0;i<12;++i)
{
int time=now.step;
temp.row=now.row+num[i][0];
temp.col=now.col+num[i][1];
if(temp.row<0||temp.col<0||temp.row>100||temp.col>100) continue;//防止产生非法数据
if(visit[temp.row][temp.col]) continue;
temp.step=time+1;
visit[temp.row][temp.col]=true;
if(temp.row==1&&temp.col==1)
{
printf("%d\n",temp.step);
return ;
}
Myqueue.push(temp);
}
}
}
int main()
{
struct ver v[2];
for(int i=0;i<2;++i)
{
scanf("%d %d",&(v[i].row),&(v[i].col));
}
BFS(v[0]);
init();
BFS(v[1]);
return 0;
}
分析
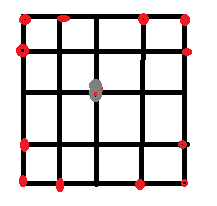
从左图可以看出,灰色的点是原点,然后周边红色的点是可以到达的点,设原点为(x,y),那么其他点就可以根据原点坐标推算出来,比如左下那个点的坐标为(x-2,y-2),一次推算下来我们可以得到一个n数组int num[][2]={{-2,-2},{-2,-1},{-1,-2},{-2,1},{-2,2},{-1,2},{1,-2},{2,-2},{2,-1},{1,2},{2,1},{2,2}};
然后进一步分析:我们可以发现有如下走法:
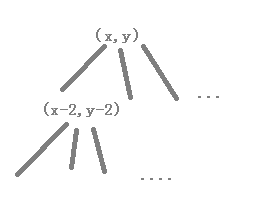
现在的问题是我们是一层一层的走呢,还是一次走到底再回来走另一条路,显然如果我们一条路走到底的方式更耗时,并且极有可能因为这条路走不通而陷入死循环,所以我们选择一层层。于是就有了以上代码。
代码中,我们首先要做的是判断数据是否已经符合,如果是,那就直接输出结果并返回,然后加上违规数据判断,判断不违规然后将该数据入队,层次遍历与队数据结构相同,故课采用队列的方式做广度优先搜索。当队列不为空的情况下循环遍历,每次取出一个数据,循环把这个数据接下来的12中走法一次入队,中间加上判断防止产生非法数据,和给已经到过的坐标打上标记,防止下次走老路(这里也是一个很重要的剪枝过程)。在后面我们直接判断本次要压入的情况是不是满足要求,是则输出数据直接返回,不是就入队,这里也减少了很多不必要的操作
总结模板:
1.判断边界条件,现在的数据是否已经符合要求
2.判断是否为非法数据
3.入队,并循环不为空
4.判断是否违法
5.判断是否标记,如果没有则标记
6.判断是否所求结果,是则返回,否则入队




 浙公网安备 33010602011771号
浙公网安备 33010602011771号