0.PTA得分截图

学习内容总结
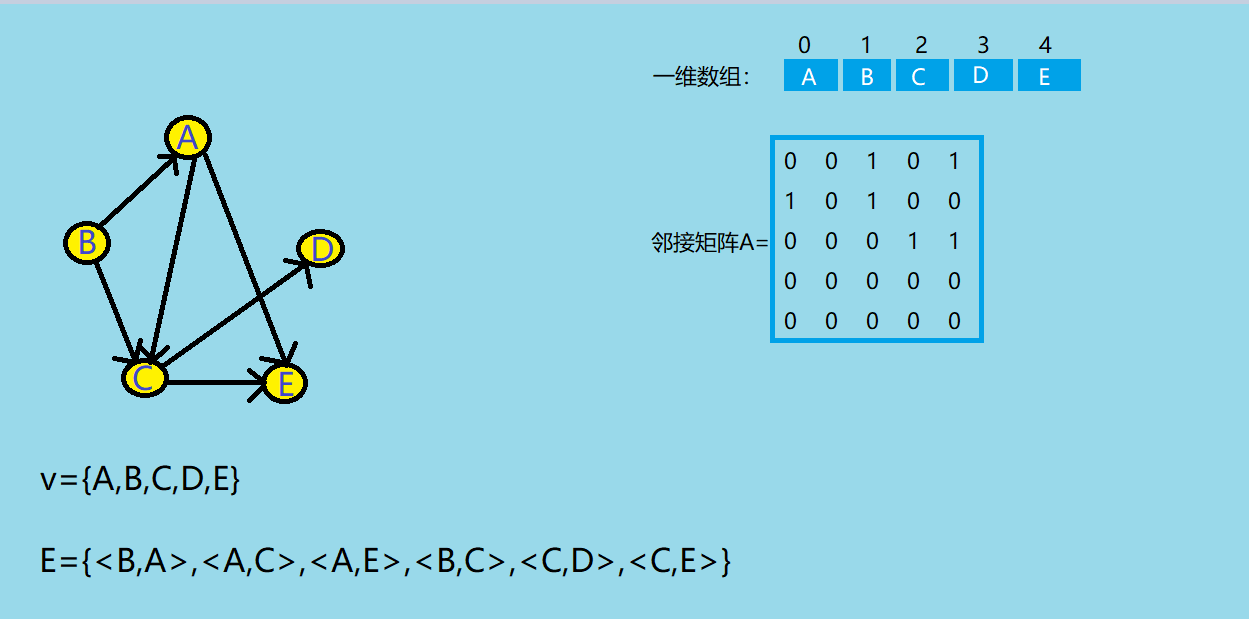
邻接矩阵法
- 节点数为n的图G = (V,E)的邻接矩阵A是n*n
- 将G的顶点编号为v1,v2...Vn(数组下标)
- 若<Vi,Vj>是E(G)z中的边时,则A[i][j]=1,否则A[i][j]=0
![]()
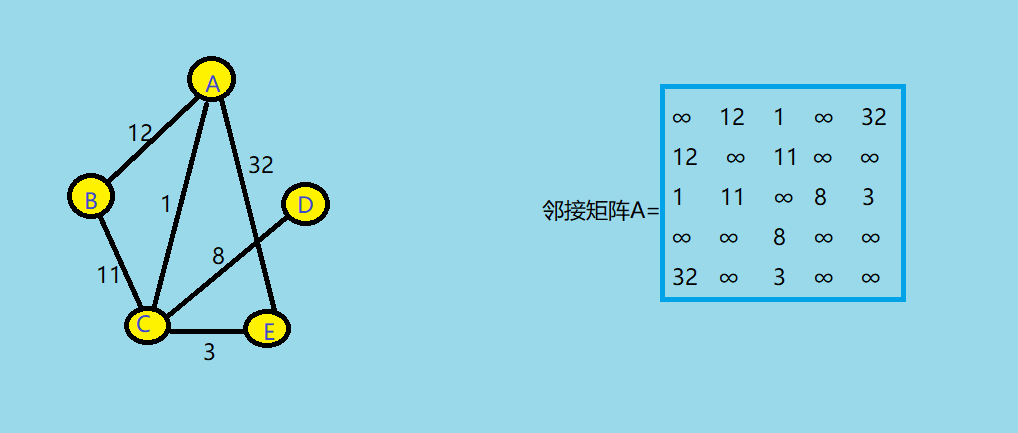
- 若图带有权重,则有<Vi,Vj>是E(G)z中的边时,A[i][j]=权重的值,否则A[i][j]=∞
![]()
图的完整邻接矩阵类型的声明如下:

总结
- 邻接矩阵法的空间复杂度为O(n^2),适合用于稠密图。
- 无向图的邻接矩阵为对称矩阵。
- 无向图中第i行(或第i列)非0元素的个数为第i个顶点的度。
- 有向图中第i行(第i列)非0元素的个数为第i个顶点的出度(入度)。
邻接表法
- 顶点表:采用顺序存储,每个数组元素存放顶点的数据和边表的头指针
- 边表:采用链式存储,单链表中存放与一个顶点相邻的所有边,一个链表结点表示一条从该顶点到链表结点顶点的边
![]()
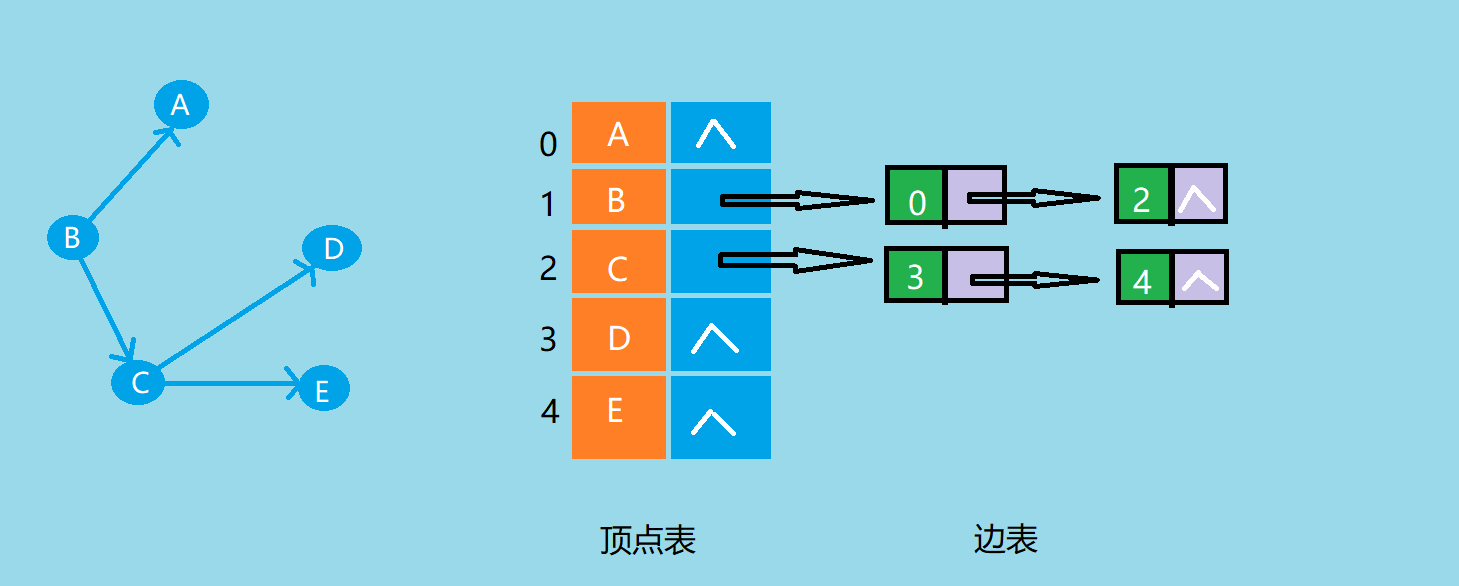
- 有向图的邻接表
![]()
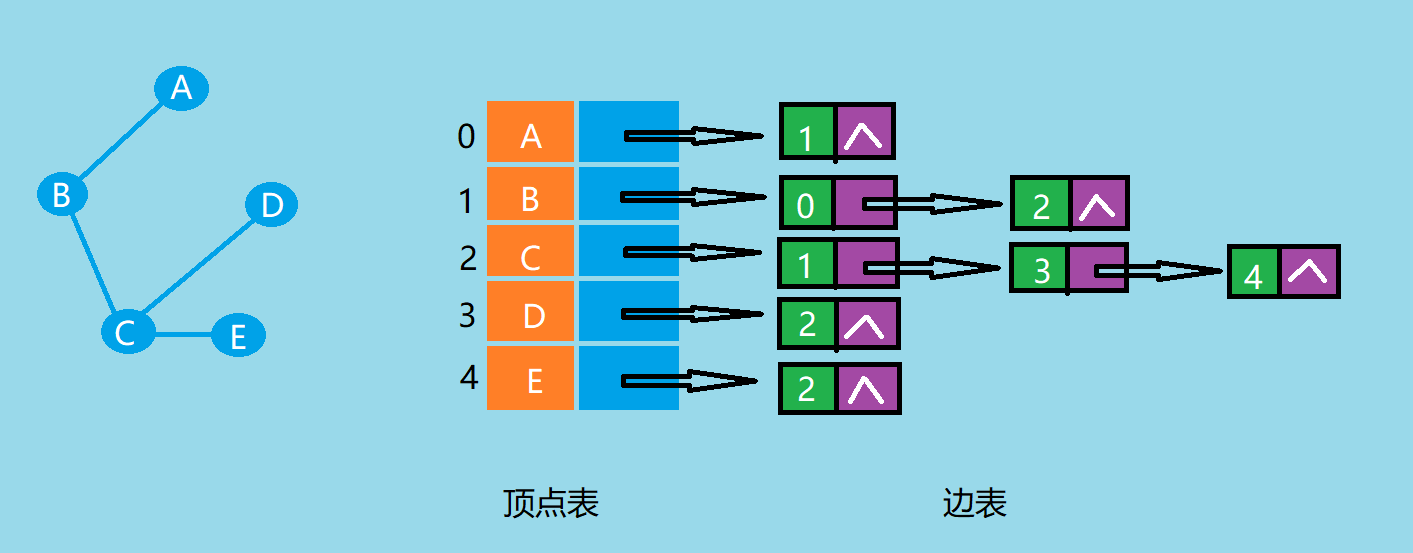
- 无向图的邻接表
![]()
- 无向带权图的邻接表
![]()
![]()
图的完整邻接表法存储类型声明:
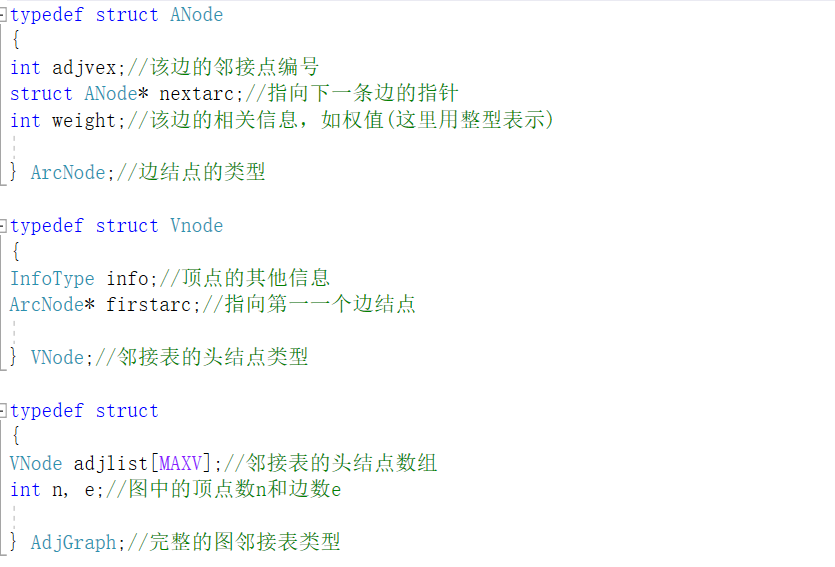
创建无向图的邻接矩阵

创建无向图的邻接表
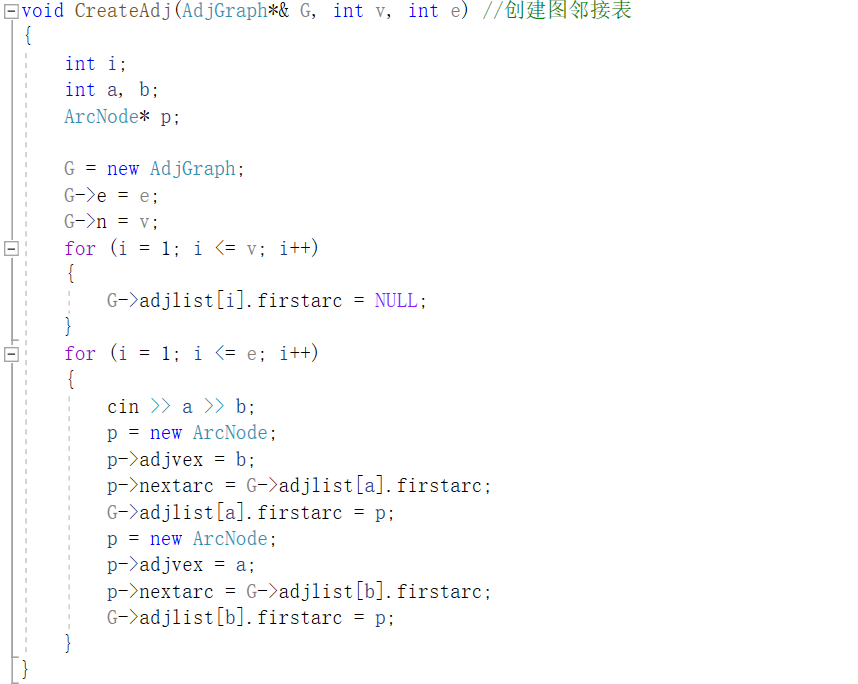
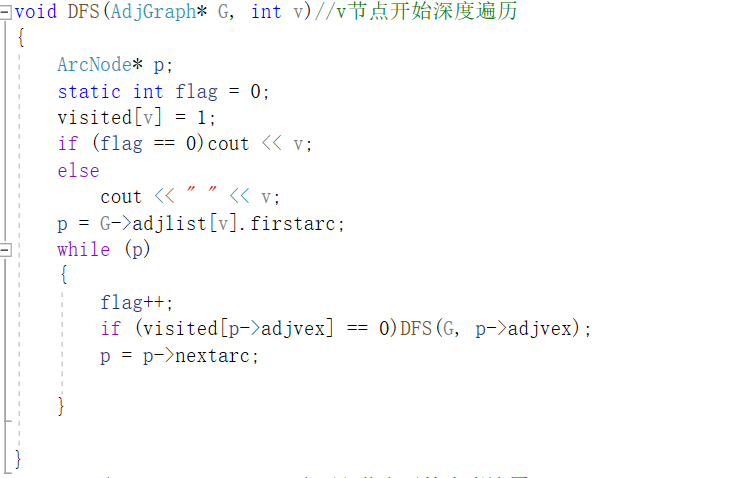
深度优先搜索
以邻接表存储结构实现无向图的深度遍历
以邻接矩阵存储结构实现无向图的深度遍历

广度优先搜索
以邻接表存储结构实现无向图的广度遍历

以邻接矩阵存储结构实现无向图的广度遍历

最小生成树
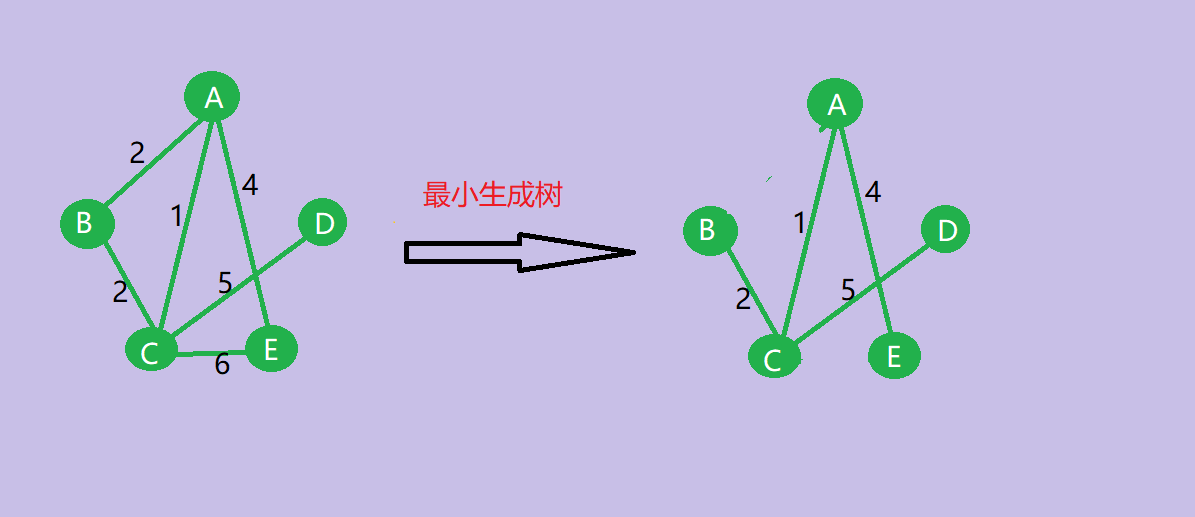
- 1.最小生成树的树形不一定唯一,当带权无向连通图G的各边权值不等时或G只有结点数减1条边时,最小生成树唯一。
- 2.最小生成树的权是唯一也是最小的。
- 3.最小生成树的边数为顶点数减1
Prim算法
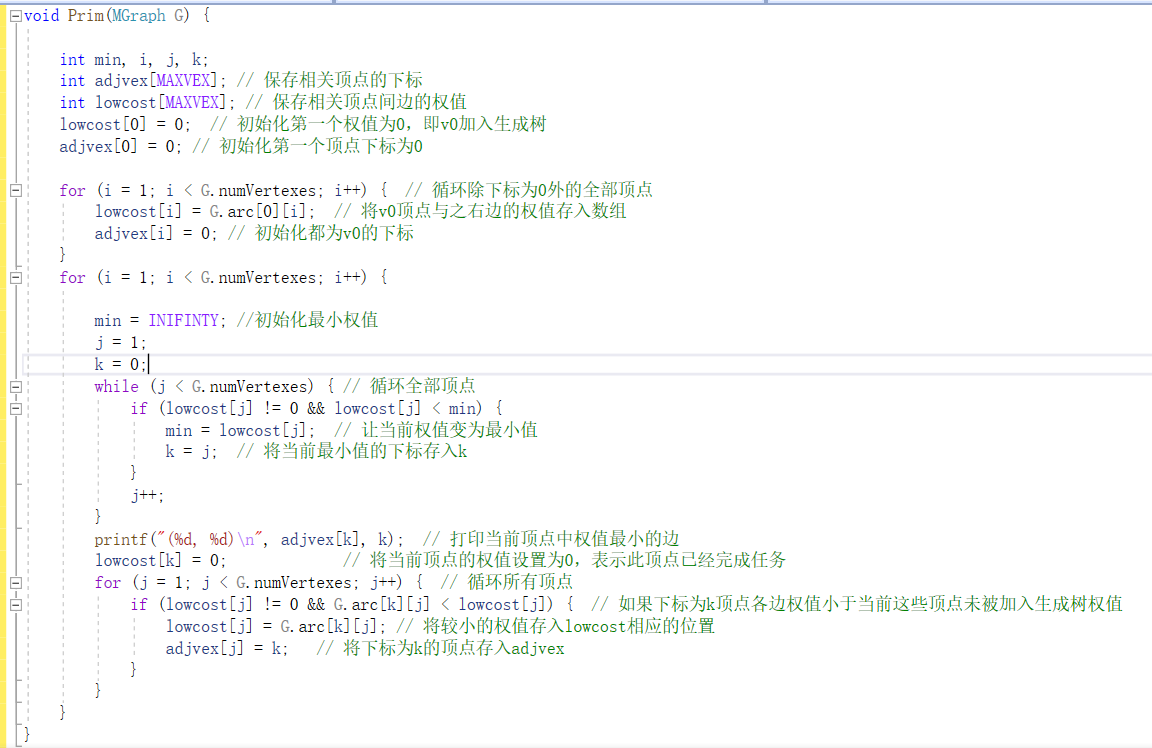
Kruskal算法
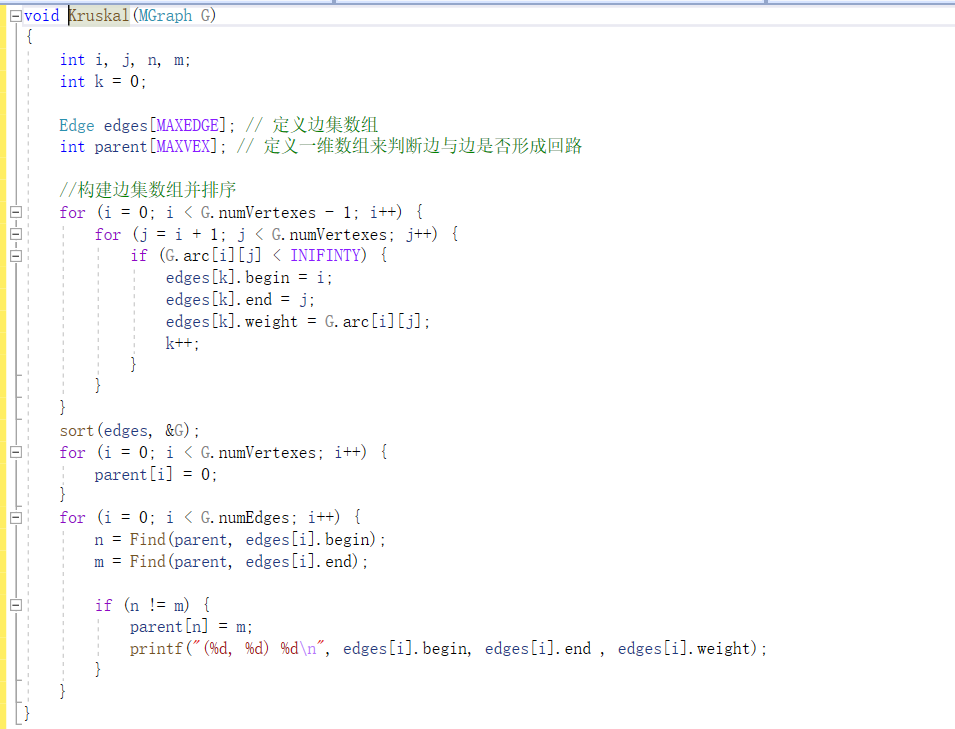
最短路径
Dijkstra算法
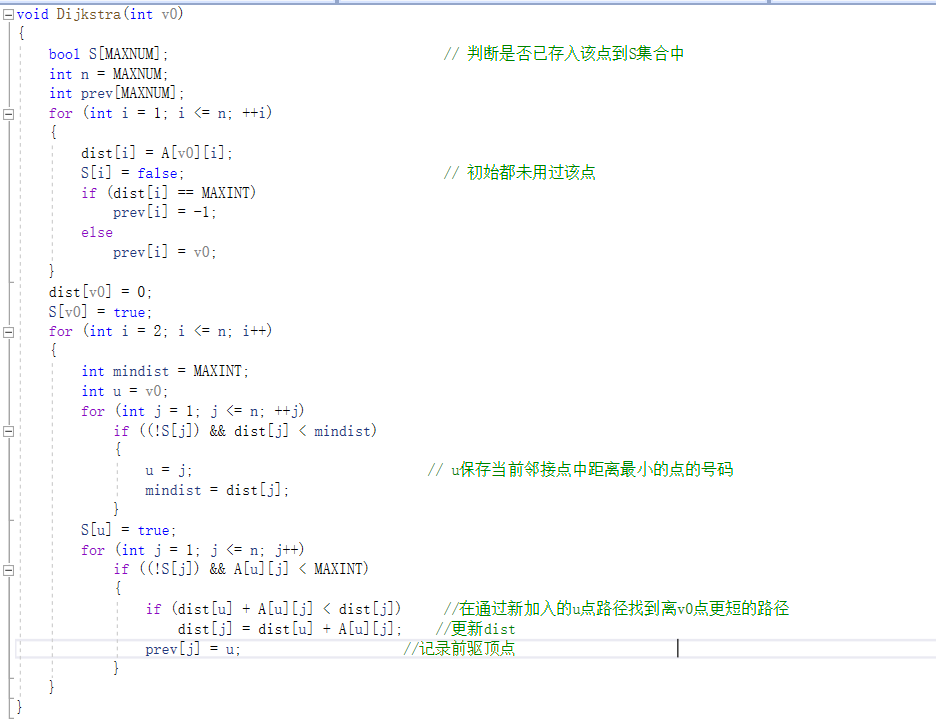
Floyd算法

拓扑排序
- 其算法思想是从图中选择一个没有前驱的顶点并输出,然后再从图中删除该顶点和所有以它为起点的有向边。重复以上步骤直到图为空或当前图中不存在无前驱的节点为为止,若执行拓扑排序算法结束后存在未访问过的节点,则说明图中有环。
![]()
拓扑排序算法
- 用队列来实现此算法,首先记录下每个节点的入度,然后将入度为0的节点入队。依次将入度为0的节点进行删边操作,再将新的入度为0的节点入队,重复以上步骤直到队空。
![]()
关键路径
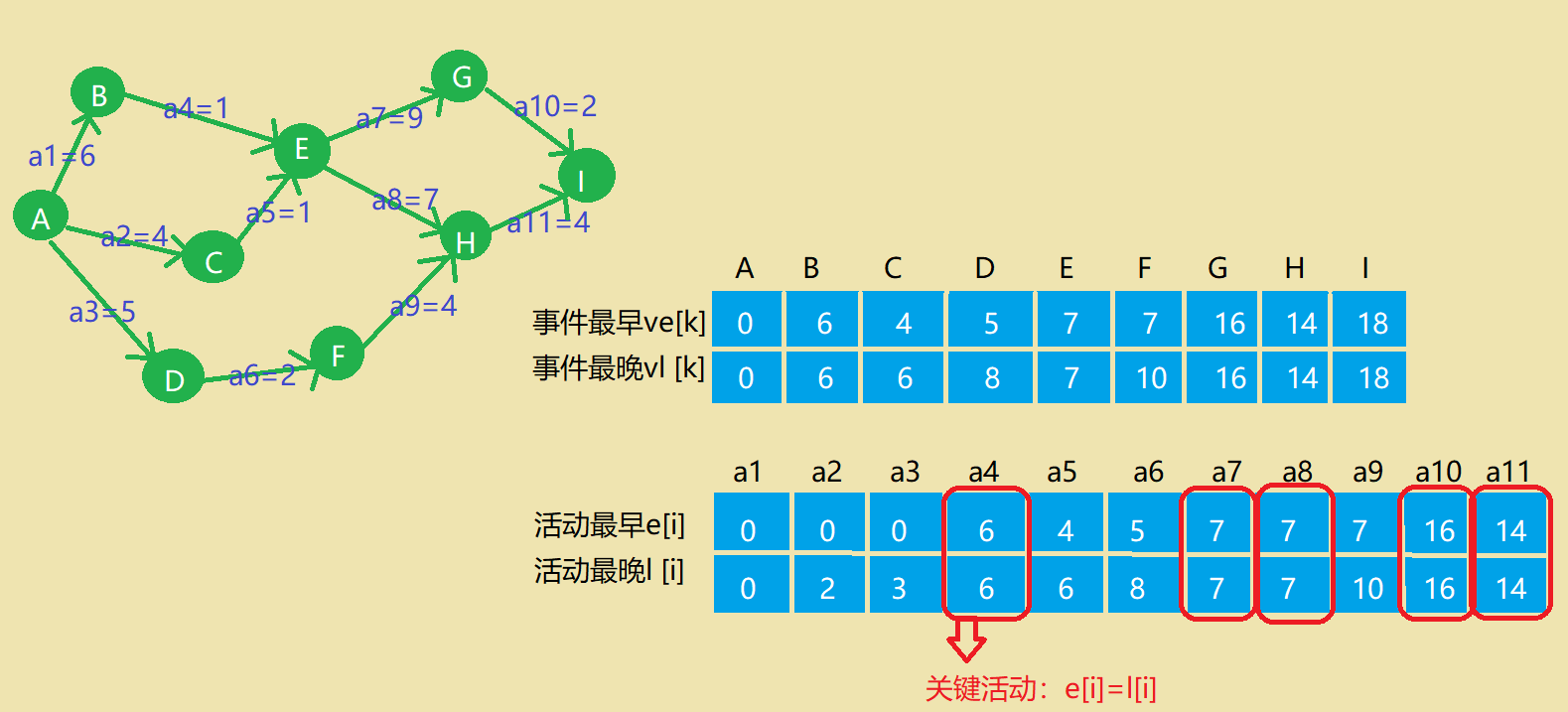
1.2.谈谈你对图的认识及学习体会。
- 本章学习了一些经典的算法,其中深度优先遍历是类似于树的层次遍历,通常使用递归实现,而广度优先遍历则类似于树的先序遍历,需要借助队列来实现。深度优先遍历和广度优先遍历都可以用邻接表和邻接矩阵为存储结构。构建最小生成树的算法主要是Prim算法和Kruscal算法,Prim算法需要多次取临边的权重的最小值,而Kruscal算法需要对权重进行排序后查找,其时间复杂度更小。
2.阅读代码
2.1 题目:Leetcode210.课程表2
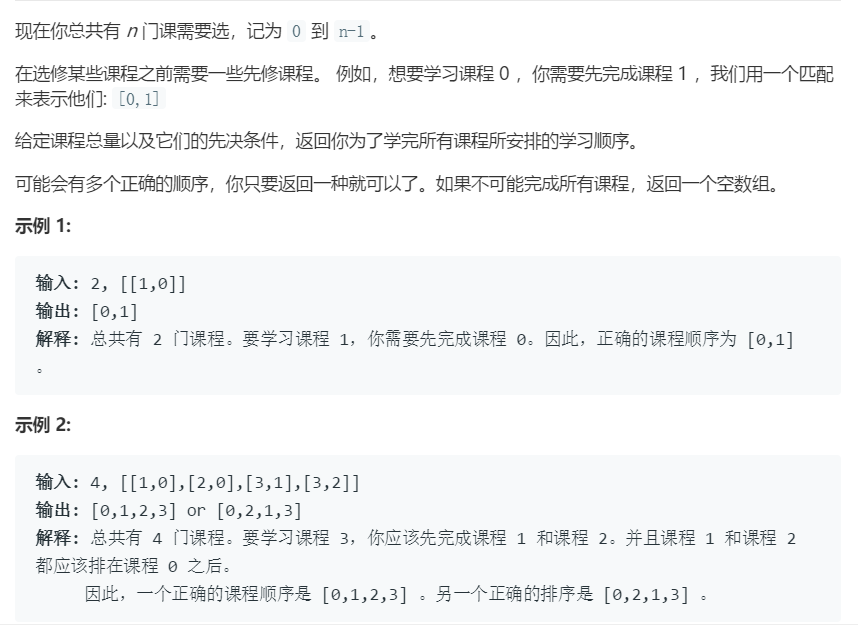
解题代码:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites)
{
vector<int> inDegree(numCourses, 0);
vector<vector<int>> lst(numCourses, vector<int>());
for (auto v : prerequisites)
{
inDegree[v[0]]++;
lst[v[1]].push_back(v[0]);
}
queue<int> que;
for (auto i = 0; i < inDegree.size(); i++)
{
if (inDegree[i] == 0)
{
que.push(i);
}
}
vector<int> ans;
while (!que.empty())
{
auto q = que.front();
que.pop();
ans.push_back(q);
for (auto l : lst[q])
{
if (--inDegree[l] == 0)
{
que.push(l);
}
}
}
return (ans.size() == numCourses) ? ans : vector<int>();
}
2.1.1 该题的设计思路
- 用拓扑排序算法实现,从图中找出所有入度为0的顶点,放入队列。每次从队列取出一个结点,从图中删除该顶点以及所有以它为起点的有向边。每删除一条有边,该边的终结点的入度-1,如果入度为0,将终结点加入队列。重复以上步骤,直到队列为空。如果拓扑排序算法执行完毕,但是和总结点数不符,说明有些结点形成环。
2.1.2 该题的伪代码
vector<int> inDegree(numCourses, 0);//用于保存课程矩阵
for i=0 to prerequisites
{
将所有课程先决条件保存进矩阵并转换为矩阵中的弧
}
vector<int> ans;//保存即将要学习的课程序号
for i=0 to inDegree.size()
{
if(此课程不需要先决条件)
将可以学习的课程放入队列
}
while(队不空)
{
取队头元素进行学习并将其出队,然后放入已学顺序容器中
}
2.1.3 运行结果
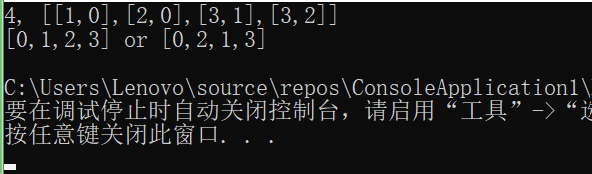
2.1.4分析该题目解题优势及难点。
- 优势是运用容器和队列辅助进行解题,效率比较高。难点在于其输入的课程先决条件是由边缘列表示的图形,并非邻接矩阵,还需要考虑输入的先决条件有没有重复的边。
2.2 题目:Leetcode332.重新安排行程

具体代码:

2.2.1 该题的设计思路
- 用Hierholzer 算法来实现,从度数为奇数的点开始遍历,逐个找回路,并通过回溯,将回路末端到下一个回溯的入口,加入最后确定的路线中。
2.2.3 运行结果

2.2.4分析该题目解题优势及难点。
- 本题运用到深度优先遍历和图的邻接表存储结构,整体代码精简了许多。难点是Hierholzer 算法的理解与实现,特别注意的是本题有重复的边,所以边的标记不能用0或1标记。
2.3 题目:Leetcode684.冗余连接

具体代码:

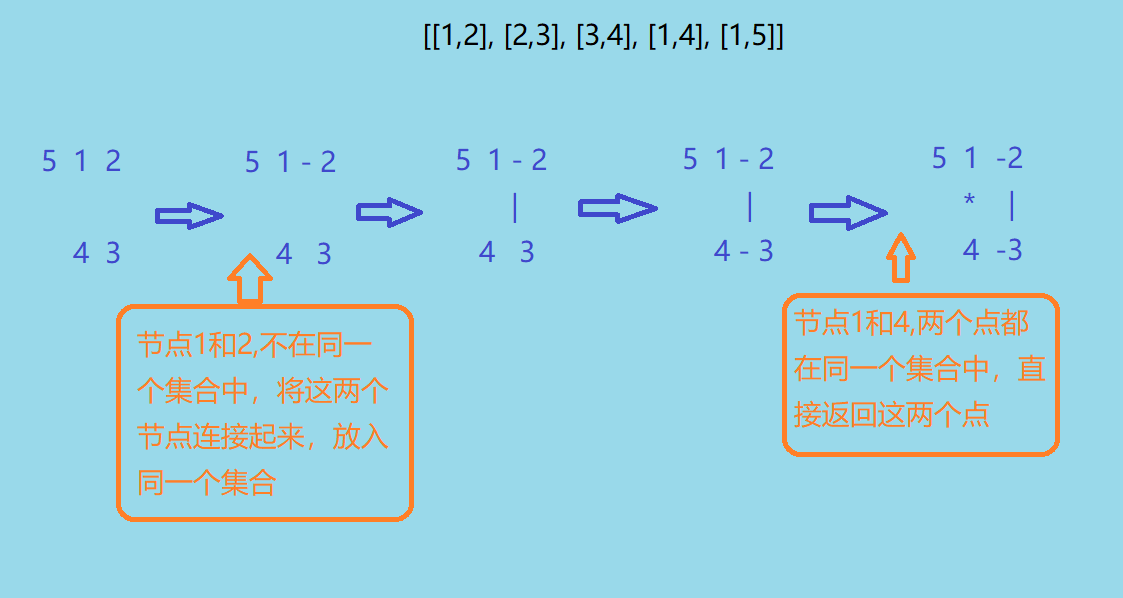
2.3.1 该题的设计思路
- 先初始化,然后遍历每一条边,如果这条边的两个节点在同一个集合中,说明它们连接后将成环,因此是那条附加的边
否则,将这两个节点连接起来,即放入同一个集合。
![]()
2.3.2 该题的伪代码
将输入的元素初始化,作为一个单独的集合
for(j=0 to sz)
{
分别寻找一条边的俩节点所在集合
if(俩节点相同)
直接返回这俩个点
else
将这两个节点连接起来,即放入同一个集合
}
2.3.3 运行结果
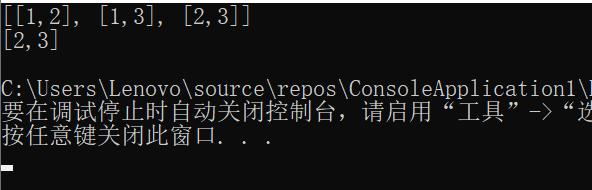
2.3.4分析该题目解题优势及难点。
- 本题运用并查集解题,思路比较好理解。难点是我们怎么把有N个节点带环的无向图通过去掉一个边使它变成N个节点的树,需要考虑去的那条边的俩个节点都被其他节点连接。







 浙公网安备 33010602011771号
浙公网安备 33010602011771号