优化深度神经网络(三)Batch Normalization
Coursera吴恩达《优化深度神经网络》课程笔记(3)-- 超参数调试、Batch正则化和编程框架
1. Tuning Process
深度神经网络需要调试的超参数(Hyperparameters)较多,包括:
:学习因子
:动量梯度下降因子
:Adam算法参数
- #layers:神经网络层数
- #hidden units:各隐藏层神经元个数
- learning rate decay:学习因子下降参数
- mini-batch size:批量训练样本包含的样本个数
超参数之间也有重要性差异。
1.通常来说,学习因子 是最重要的超参数,也是需要重点调试的超参数。
2.动量梯度下降因子 、各隐藏层神经元个数#hidden units和mini-batch size的重要性仅次于
。
3.神经网络层数#layers和学习因子下降参数learning rate decay。
4.Adam算法的三个参数 一般常设置为0.9,0.999和
,不需要反复调试。
当然,这里超参数重要性的排名并不是绝对的,具体情况,具体分析。
4. Batch Normalization
在训练神经网络时,标准化输入可以提高训练的速度。方法是对训练数据集进行归一化的操作,即将原始数据减去其均值 后,再除以其方差
。
但是标准化输入只是对输入进行了处理,那么对于神经网络,又该如何对各隐藏层的输入进行标准化处理呢?
其实在神经网络中,第 层隐藏层的输入就是第
层隐藏层的输出
。对
进行标准化处理,从原理上来说可以提高
和
的训练速度和准确度。这种对各隐藏层的标准化处理就是Batch Normalization。值得注意的是,实际应用中,一般是对
进行标准化处理而不是
,其实差别不是很大。
Batch Normalization对第 层隐藏层的输入
做如下标准化处理,忽略上标
:单层
其中,m是单个mini-batch包含样本个数, 是为了防止分母为零,可取值
。这样,使得该隐藏层的所有输入
均值为0,方差为1。
但是,大部分情况下并不希望所有的 均值都为0,方差都为1,也不太合理。通常需要对
进行进一步处理:
上式中, 和
是可学习参数,类似于W和b一样,可以通过梯度下降等算法求得。这里,
和
的作用是让
的均值和方差为任意值,只需调整其值就可以了。
例如,令:
, 则
,即他们两恒等。
可见,设置 和
为不同的值,可以得到任意的均值和方差。
这样,通过Batch Normalization,对隐藏层的各个 进行标准化处理,得到
,替代
。
输入的标准化处理Normalizing inputs和隐藏层的标准化处理Batch Normalization是有区别的:
Normalizing inputs使所有输入的均值为0,方差为1。而Batch Normalization可使各隐藏层输入的均值和方差为任意值。实际上,从激活函数的角度来说,如果各隐藏层的输入均值在靠近0的区域即处于激活函数的线性区域,这样不利于训练好的非线性神经网络,得到的模型效果也不会太好。这也解释了为什么需要用 和
来对
作进一步处理。
Batch Norm经常使用在mini-batch上,这也是其名称的由来。
值得注意的是,因为Batch Norm对各隐藏层 有去均值的操作,所以这里的常数项
可以消去,其数值效果完全可以由
中的
来实现。因此,我们在使用Batch Norm的时候,可以忽略各隐藏层的常数项
。在使用梯度下降算法时,分别对
,
和
进行迭代更新。
除了传统的梯度下降算法之外,还可以使用我们之前介绍过的动量梯度下降、RMSprop或者Adam等优化算法。
BN算法 在训练中对于一个mini-batch

Algorithm 1: Batch Normalizing Transform, applied to activation x over a mini-batch.
在训练过程中,我们还需要计算反向传播损失函数l的梯度,并且计算每个参数(注意: 和
)。 我们使用链式法则,如下所示:
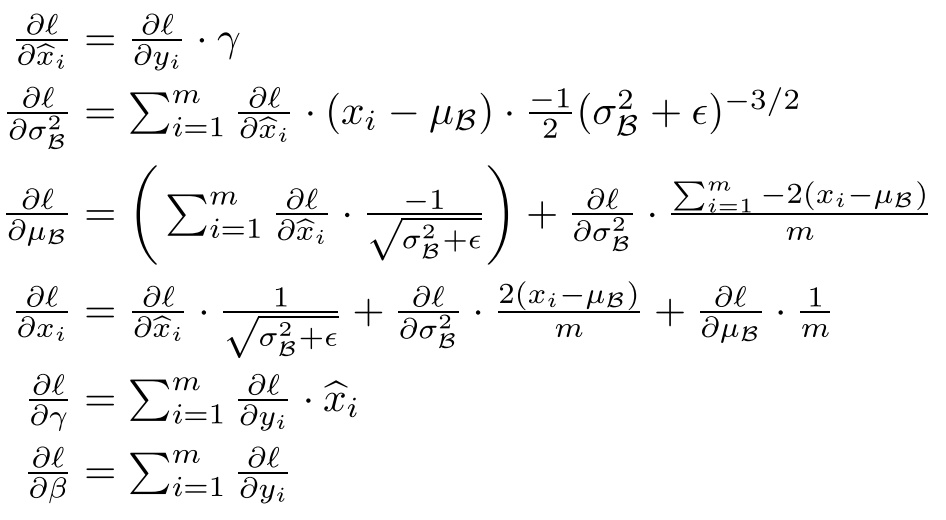
推导过程:
Batch Normalization学习笔记及其实现
BN算法在训练和测试时的应用
BN算法在训练时的操作就如我们上面所说,首先提取每次迭代时的每个mini-batch的平均值和方差进行归一化,再通过两个可学习的变量恢复要学习的特征。
但是在实际应用时就没有mini-batch了,那么BN算法怎样进行归一化呢?实际上在测试的过程中,BN算法的参数就已经固定好了,首先进行归一化时的平均值和方差分别为:
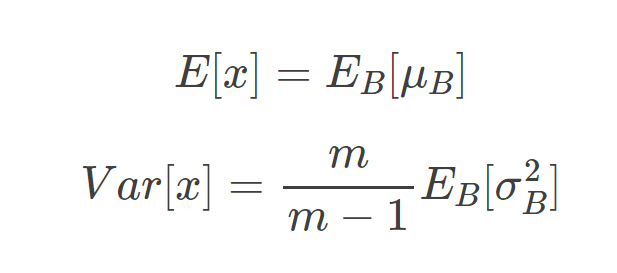
方法1:即平均值为所有mini-batch的平均值的平均值,而方差为每个batch的方差的无偏估计
方法2:估计的方法有很多,理论上我们可以将所有训练集放入最终的神经网络模型中,然后将每个隐藏层计算得到的 和
直接作为测试过程的
和
来使用。但是,实际应用中一般不使用这种方法,而是使用我们之前介绍过的指数加权平均(exponentially weighted average)的方法来预测测试过程单个样本的
和
。
指数加权平均的做法很简单,对于第 层隐藏层,考虑所有mini-batch在该隐藏层下的
和
,然后用指数加权平均的方式来预测得到当前单个样本的
和
。这样就实现了对测试过程单个样本的均值和方差估计。最后,再利用训练过程得到的
和
值计算出各层的
值。
最终BN算法的训练和测试的流程如下图所示:

第11步就是将 代入
代入![]() μ和σ要换成算法中的Ex和Varx
μ和σ要换成算法中的Ex和Varx
Batch Norm让模型更加健壮
如果实际应用的样本与训练样本分布不同,即发生了covariate shift,则一般是要对模型重新进行训练的。在神经网络,尤其是深度神经网络中,covariate shift会导致模型预测效果变差,重新训练的模型各隐藏层的 和
均产生偏移、变化。
而Batch Norm的作用恰恰是减小covariate shift的影响,让模型变得更加健壮,鲁棒性更强。
Batch Norm减少了各层 、
之间的耦合性,让各层更加独立,实现自我训练学习的效果。
也就是说,如果输入发生covariate shift,那么因为Batch Norm的作用,对个隐藏层输出 进行均值和方差的归一化处理,
和
更加稳定,使得原来的模型也有不错的表现。
论文笔记-Batch Normalization
BN优点
(1)神经网络本质是学习数据分布,如果寻来你数据与测试数据分布不同,网络的泛化能力将降低,batchnorm就是通过对每一层的计算做scale和shift的方法,通过规范化手段,把每层神经网络任意神经元这个输入值的分布强行拉回到正太分布,减小其影响,让模型更加健壮。
(2)使用BN就可以使得不同层不同scale的权重变化整体步调更一致,可以使用更高的学习率,加快训练速度。
(3) 防止过拟合。此时可以移除或使用较低的dropout,降低L2权重衰减系数等防止过拟合的手段。论文中最后的模型分别使用10%、5%和0%的dropout训练模型,与之前的40%-50%相比,可以大大提高训练速度。
(4) 取消Local Response Normalization层。 对局部神经元的活动创建竞争机制,使其中响应比较大对值变得相对更大,并抑制其他反馈较小的神经元,增强了模型的泛化能力。有了dropout,bn等手段没必要用了,而且2012一篇文章说这个lrn没有用处。
专栏 | 深度学习中的Normalization模型
CNN 网络中的 BN
我们知道,常规的 CNN 一般由卷积层、下采样层及全连接层构成。全连接层形式上与前向神经网络是一样的,所以可以采取前向神经网络中的 BatchNorm 方式,而下采样层本身不带参数所以可以忽略,所以 CNN 中主要关注卷积层如何计算 BatchNorm。
CNN 中的某个卷积层由 m 个卷积核构成,每个卷积核对三维的输入(通道数*长*宽)进行计算,激活及输出值是个二维平面(长*宽),对应一个输出通道(参考图 7),由于存在 m 个卷积核,所以输出仍然是三维的,由 m 个通道及每个通道的二维平面构成。
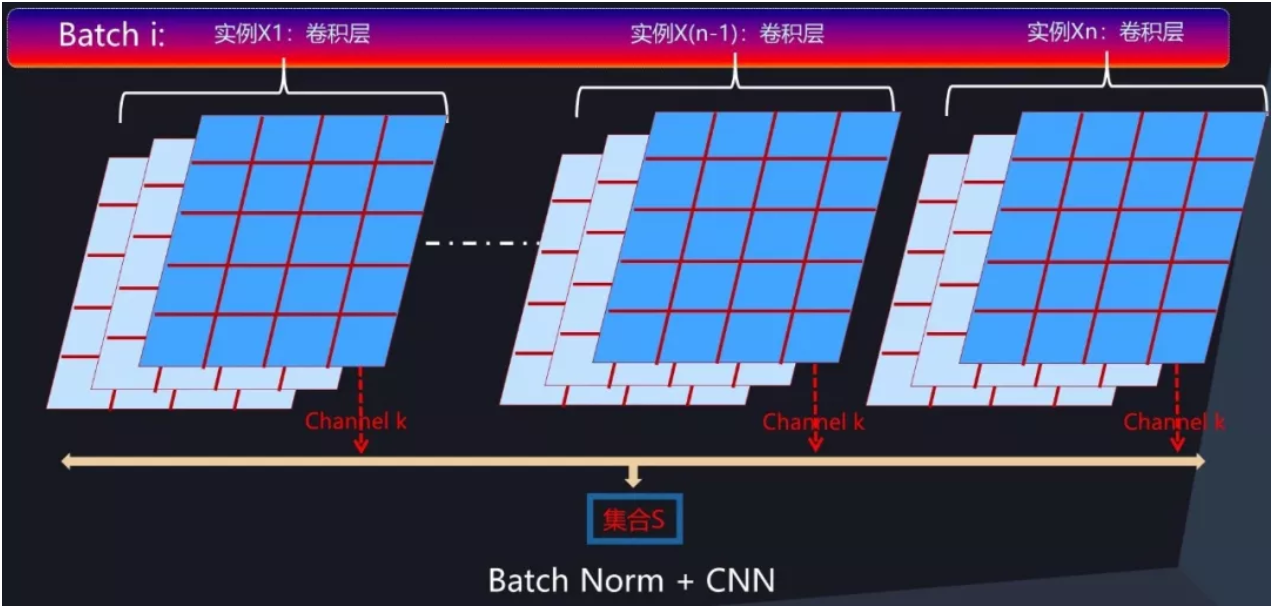
那么在卷积层中,如果要对通道激活二维平面中某个激活值进行 Normalization 操作,怎么确定集合 S(BN的E和Var是通过神经元集合S中包含的 m 个神经元各自的激活值求出的,集合S指求均值方差使用的激活值的范围) 的范围呢?图 8 给出了示意图。
类似于前向神经网络中的 BatchNorm 计算过程,对于 Mini-Batch 训练方法来说,反向传播更新梯度使用 Batch 中所有实例的梯度方向来进行,所以对于 CNN 某个卷积层对应的输出通道 k 来说,假设某个 Batch 包含 n 个训练实例,那么每个训练实例在这个通道 k 都会产生一个二维激活平面,也就是说 Batch 中 n 个训练实例分别通过同一个卷积核的输出通道 k 的时候产生了 n 个激活平面。假设激活平面长为 5,宽为 4,则激活平面包含 20 个激活值,n 个不同实例的激活平面共包含 20*n 个激活值。那么 BatchNorm 的集合 S 的范围就是由这 20*n 个同一个通道被 Batch 不同训练实例激发的激活平面中包含的所有激活值构成(对应图 8 中所有标为蓝色的激活值)。
(对于训练集的一个batch,batch的所有训练实例(一个实例是一张图片)经过同一个卷积核的输出 求均值和方差 就是BN的E和Var)
划定集合 S 的范围后,激活平面中任意一个激活值都需进行 Normalization 操作,其 Normalization 的具体计算过程与前文所述计算过程一样,采用公式 3 即可完成规范化操作。这样即完成 CNN 卷积层的 BatchNorm 转换过程。
公式3:
////////////////////////////////////////////////////////////////////////////////////////////////////
The first is that instead of whitening the features in layer inputs and outputs jointly, we will normalize each scalar feature independently, by making it have the mean of zero and the variance of 1.
 每一维
每一维
we make the second simplification: since we use mini-batches in stochastic gradient training, each mini-batch produces estimates of the mean and variance of each activation.
 minibatch中每一维有多个xk 简写x
minibatch中每一维有多个xk 简写x
 γ and β are to be learned
γ and β are to be learned
![]() 测试时是固定的参数
测试时是固定的参数
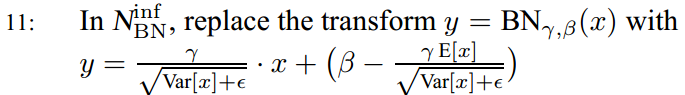 在测试时,对每一维 E和Var哪里来?
在测试时,对每一维 E和Var哪里来?



 浙公网安备 33010602011771号
浙公网安备 33010602011771号