带修改莫队浅谈

二逼平衡树写得我兹娃乱叫之时，学习了清流的算法——莫队。这次是莫队的进阶版本，资瓷单点修改操作。

原来需要的是两个关键字，而现在多了一维时间。

第一个关键字L表示查询左端点l所在的块的编号，第二个关键字R表示查询右端点r所在块的编号(并不是右端点的值了,因为还有第三维)，第三个关键字为时间t。

在这里我们是对修改操作维护的时间轴，之后在查询操作中查找离此次查询操作最近的一次修改操作的时间(请仔细思考)

如果现在的时间比需要的时间大，那么我们让时间倒流，改回原值，剩下的就交给普通莫队了。

我们来对时间复杂度进行证明。

对于一块到底是多少使得时间复杂度最优的问题，我们来分析一下。

以下是luogu题解中的内容对于t轴的移动可以保存每次修改，如果修改在(l,r)间则更新

 

分块方法可以参照原版莫队，先将l分块，再讲r分块，同一块的按t排序

 

块大小为 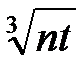可以达到最快的理论复杂度 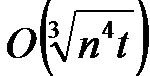，证明如下

 

设分块大小为a，莫队算法时间复杂度主要为t轴移动，同r块l,r移动，l块间的r移动三部分

 

t轴移动的复杂度为 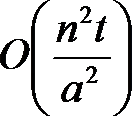，同r块l,r移动复杂度为 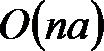，l块间的r移动复杂度为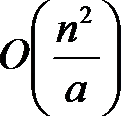

 

三个函数max的最小值当a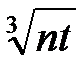为 取得，为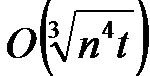

综上所述，一块大小为√n³。

我们直接用STL解决

size=pow(n,0.67);

 HH的项链的进阶版，多了个单点修改

P1903 [国家集训队]数颜色 / 维护队列

// luogu-judger-enable-o2
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
#define N 50010
int size;
int n,Q;
struct Query
{
    int blobx,bloby,x,y,daan,id,pre;
}query[N];
struct Change
{
    int pos,color;
}change[N];
int a[N];
int col[N];
int sum[1000100];
int ans;
char q[3];
int idx,idx2;
int x,y;
bool cmp(const Query &a,const Query &b)
{
    if(a.blobx!=b.blobx)
        return a.blobx<b.blobx;
    if(a.bloby!=b.bloby)
        return a.bloby<b.bloby;
    return a.id<b.id;
}
bool cmp2(const Query &a,const Query &b)
{
    return a.id<b.id;
}
int calc(int x)
{
    if(x%size==0)
        return x/size;
    else
        return x/size+1;
}
void del(int x)
{
    if(--sum[a[x]]==0)
        ans--;
}
void add(int x)
{
    if(++sum[a[x]]==1)
        ans++;
}
void go(int now,int i)
{
    if(change[now].pos>=query[i].x&&change[now].pos<=query[i].y)
    {
        if(--sum[a[change[now].pos]]==0)
            ans--;
        if(++sum[change[now].color]==1)
            ans++;
    }
    swap(a[change[now].pos],change[now].color);
}
int main()
{
    scanf("%d%d",&n,&Q);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    size=pow(n,0.67);
    for(int i=1;i<=Q;i++)
    {
        scanf("%s",q);
        if(q[0]=='Q')
        {
            scanf("%d%d",&x,&y);
            query[++idx].x=x;
            query[idx].y=y;
            query[idx].blobx=calc(query[idx].x);
            query[idx].bloby=calc(query[idx].y);
            query[idx].id=idx;
            query[idx].pre=idx2;
        }
        else
        {
            scanf("%d%d",&x,&y);
            change[++idx2].pos=x;
            change[idx2].color=y;
        }
    }
    sort(query+1,query+idx+1,cmp);
    int l=1,r=0,tim=0;
    for(int i=1;i<=idx;i++)
    {
        while(l<query[i].x)
            del(l++);
        while(l>query[i].x)
            add(--l);
        while(r<query[i].y)
            add(++r);
        while(r>query[i].y)
            del(r--);
        while(tim<query[i].pre)
            go(++tim,i);
        while(tim>query[i].pre)
            go(tim--,i);
        query[i].daan=ans;
    }
    sort(query+1,query+idx+1,cmp2);
    for(int i=1;i<=idx;i++)
        printf("%d\n",query[i].daan);
}