树，二叉树及算法总结

 一、思维导图

 

 

 

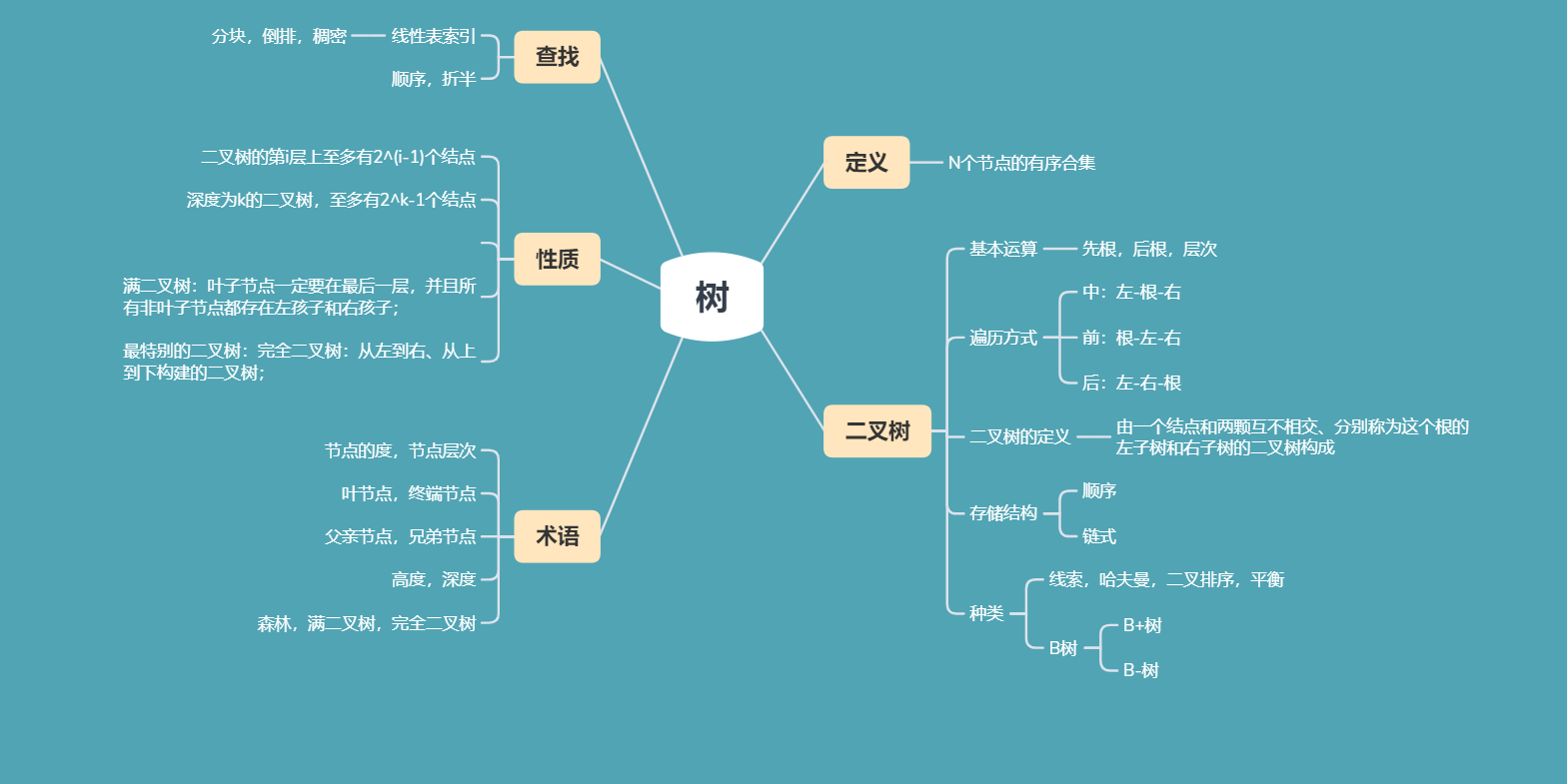
 二、概念笔记：

一、满二叉树

  1.叶子只能出现在最下一层；
  2.只有度为0和度为2的结点。
　  注意　：满二叉树在同样深度的二叉树中结点个数最多

　　　　　  满二叉树在同样深度的二叉树中叶子结点个数最多

 二、完全二叉树 

    1. 叶子结点只能出现在最下两层，且最下层的叶子结点都集中在二叉树的左部；

     2. 完全二叉树中如果有度为1的结点，只可能有一个，且该结点只有左孩子。

      3. 深度为k的完全二叉树在k-1层上一定是满二叉树。

 

三、完全二叉树的基本性质

      1、有n个节点的完全二叉树的深度为 k=log2n。

      2、 i层的节点数目为：2^i

　  3、最后一层的节点数为：n−(2k−1)=n+1−2kn−(2k−1)=n+1−2k

四、二叉树的基本性质

    1、二叉树的第i层上最多有2的i-1次方个结点（i≥1）。 

     2、一棵深度为k的二叉树中，最多有2的k次方-1个结点，最少有k个结点。

     3、深度为k且具有2k-1个结点的二叉树一定是满二叉树，

     4、在一棵二叉树中，如果叶子结点数为n0，度为2的结点数为n2，则有: n0＝n2＋1。

五、树的遍历：

​ 　 1、先根遍历：先访问根结点，再从左往右遍历根结点的子树。

​      2、后根遍历：先从左往右遍历根结点的子树，再访问根结点。

​     3、层次遍历：从根结点开始，从上到下，从左到右，访问每个结点

六、树的存储结构

　　1、双亲表示法：除了根结点没有父结点外，其余每个结点都有一个唯一的父结点。将所有结点存到一个数组中。每个结点都有一个数据域data和一个                数值parent指示其双亲在数组中存放的位置。

　　2、链式存储结构：就是用链表来表示一棵二叉树，即用链表来指示元素之间的逻辑关系。

　　　　通常有两种存储形式：

           链表中每个结点由三个域组成，除了数据域之外，还有两个指针域，分别用来给出该结点的左孩子和右孩子所在的存储地址。

　　　链表中每个结点由四个域组成，除了数据域之外，还有三个指针域，分别用来给出该结点的左孩子、右孩子和双亲结点所在的存储地址。

七、线索二叉树：

　　1、使每个结点都有了唯一前驱和后继（第一个结点无前驱，最后一个结点无）

　　2、节约空间，但是插入和删除慢

八、哈夫曼树：

 

　　带权路径长度WPL最小的二叉树称为哈夫曼树WPL=所有（叶子结点的权值*路径长度）之和。

九、二叉排序树

　　1、若左子树不空，则左子树上所有结点的值均小于它的根结点的值

　　2、若右子树不空，则右子树上所有结点的值均大于它的根结点的值；

　　3、n个节点的该树平均查找长度为O（log2n）

十、平衡树：

   每个结点的左、右子树的高度最多相差1的二叉树叫做平衡树。

三、疑难问题及解决方案

平衡二叉树问题

解决方法：通过网上查看类似问题详解解决

将 2，1，0，3，4，5，6，9，8，7依次构造平衡二叉树。

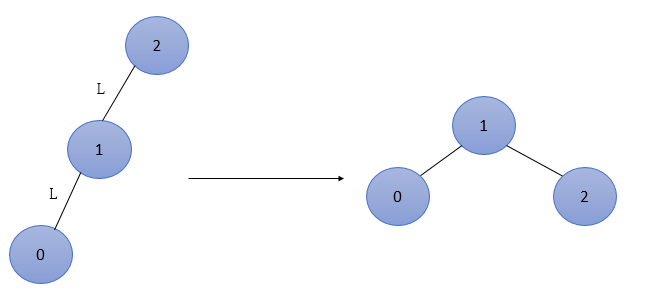
首先数据为2的结点作为根结点插入，接着插入1，仍是平衡的，再插入0是，2的平衡因子变为2，此时出现了不平衡，因此需要进行调整，最低不平衡结点为2，属于LL型，调整过程如图1所示。

图1

 

 

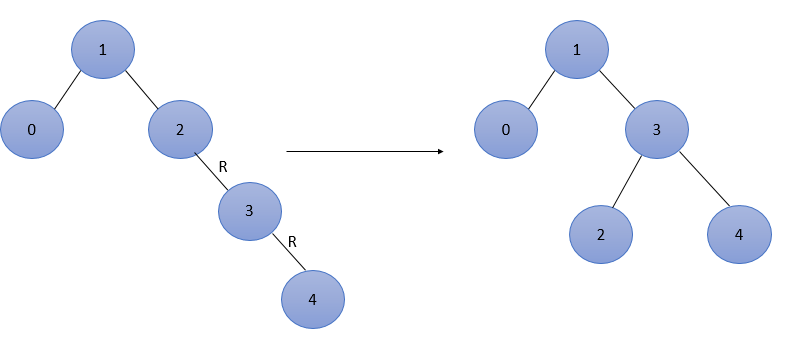
接着插入3，是平衡的，再插入4，此时出现了不平衡，结点 1 和 2 的平衡因子都为 -2，结点2为最低不平衡结点，属于RR型，调整过程如图2所示

图2

 

 

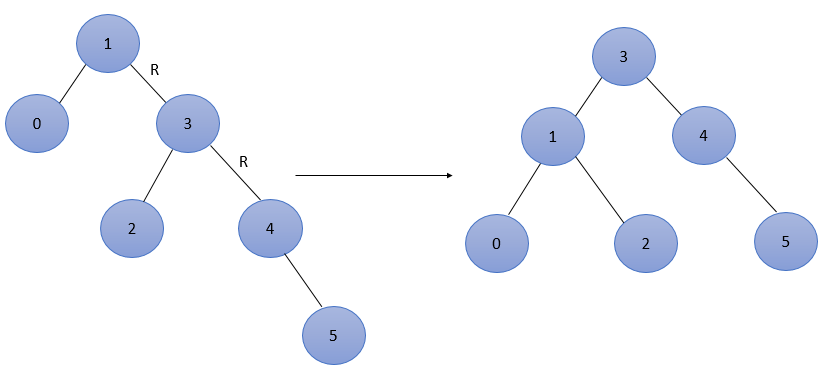
接着插入5，此时结点 1 的平衡因子为 -2，导致不平衡，结点1为最低不平衡结点，属于RR型，调整如图3所示。

图3

 

 

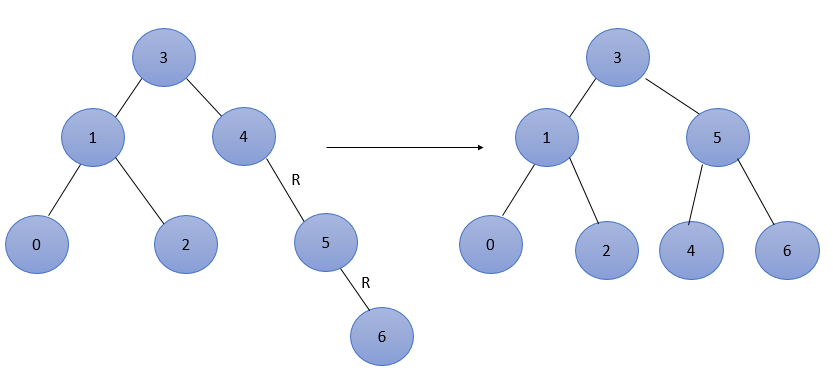
接着插入6，此时结点4的平衡因子为 -2，导致不平衡，结点4为最低不平衡结点，属于RR型，调整如图4所示。

图4

 

 

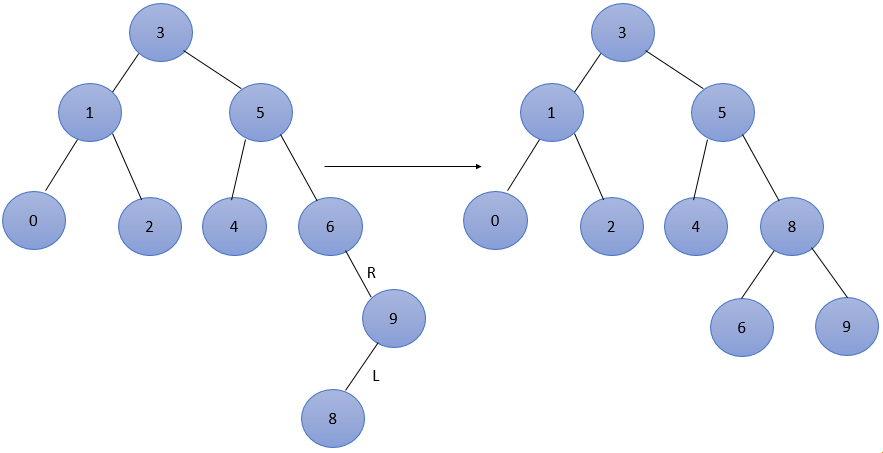
接着插入9，是平衡的，再插入8，此时结点 3、5、6 的平衡因子都为 -2，导致不平衡，结点6为最低不平衡结点，属于RL型，调整如图5所示。

图五

 

 

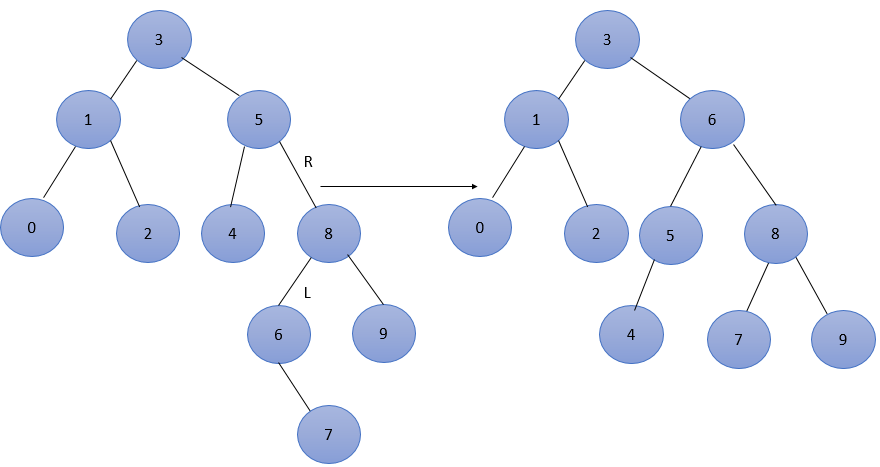
插入7，此时结点3、5的平衡因子为 -2，导致不平衡，最低不平衡结点为5，属于RL型，调整如图6所示。