汉诺塔

递归的理解：

函数的调用 ， 也是进栈出栈的过程 ， 所以有栈的特性 ：  保留所有的实在参数，返回地址等信息（ 保留这一层的所有的信息），每一层递归所需的信息构成一个“工作区域”，每进一层递归，就产生一个新的工作区域  。  return或者函数结束，标志着 递归函数“归” 到上一层的过程 ， 同时变量也更新为上一层的变量值 。 在递归嵌套时 ， 往往难考虑递归内部 具体的 进程 ， 所以我们只需要用经验知道这个 问题更够 利用 递归解决 ， 并且 写好 基线情况 ， 和最简单的情况 ， 就能够将 较大的规模的问题解决 。 

下面结合汉诺塔问题加深一下理解 ：  汉诺塔问题解决的套路就是 里面的 双重递归 （快排 ， 二叉树遍历）也都涉及 ， 所以通过递归搜索树更能直观的看出  。

 

1 void hanio( int  n ,  char x , char y , char z )  
 2 {
 3 if( n ==1  )  
 4 { move( x , 1 , z ) ;   // 其实move 在这里 并没有什么用 ， 只是 打印一下，把注意力 放在 双重递归

 5 else

 6 {
 7 hanio(n-1 ,  x, z, y ) ;

    move( x , n , z )  ;
 8 hanio( n - 1  , y , x ,z )  ;
 9 
10 }
11 return ; 
12 }

 

 

 

1. 确定基线情况 ： 也就是 只有一个的情况 ,  x--> z 即可 。 
2. 确定最简单的情况 ， 如何形成一个 最简单的二叉树  如图 ： 
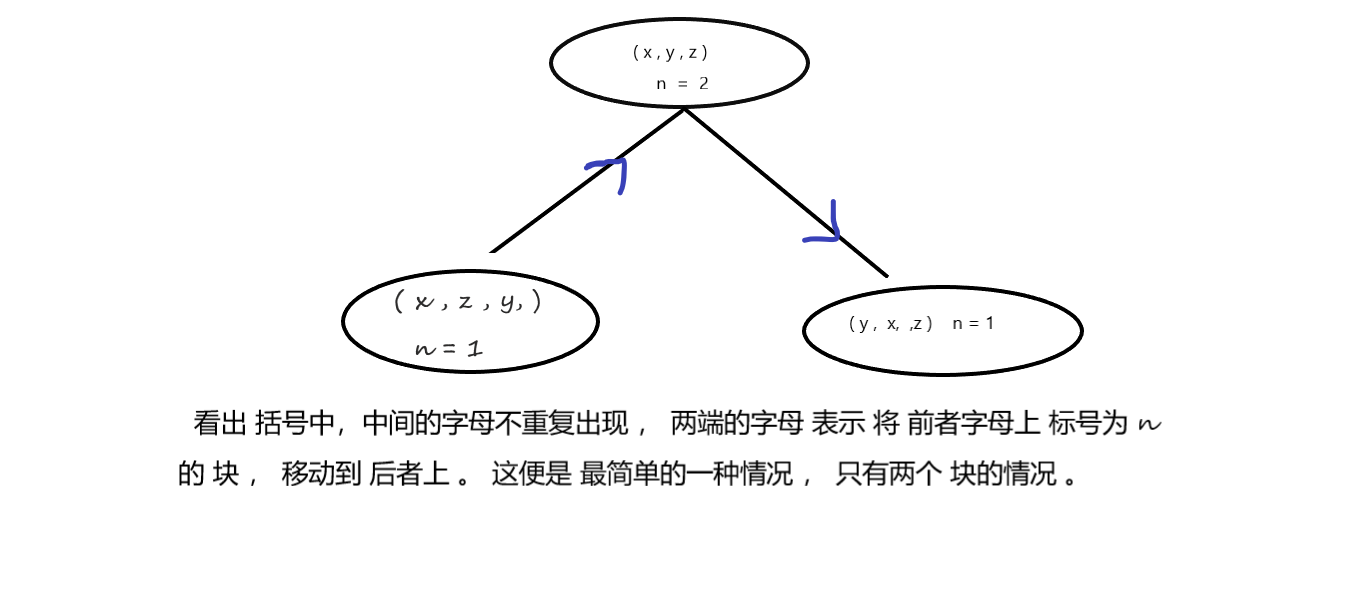
3. 下面：模拟一下 n ==3 的 情况 ：
4. 

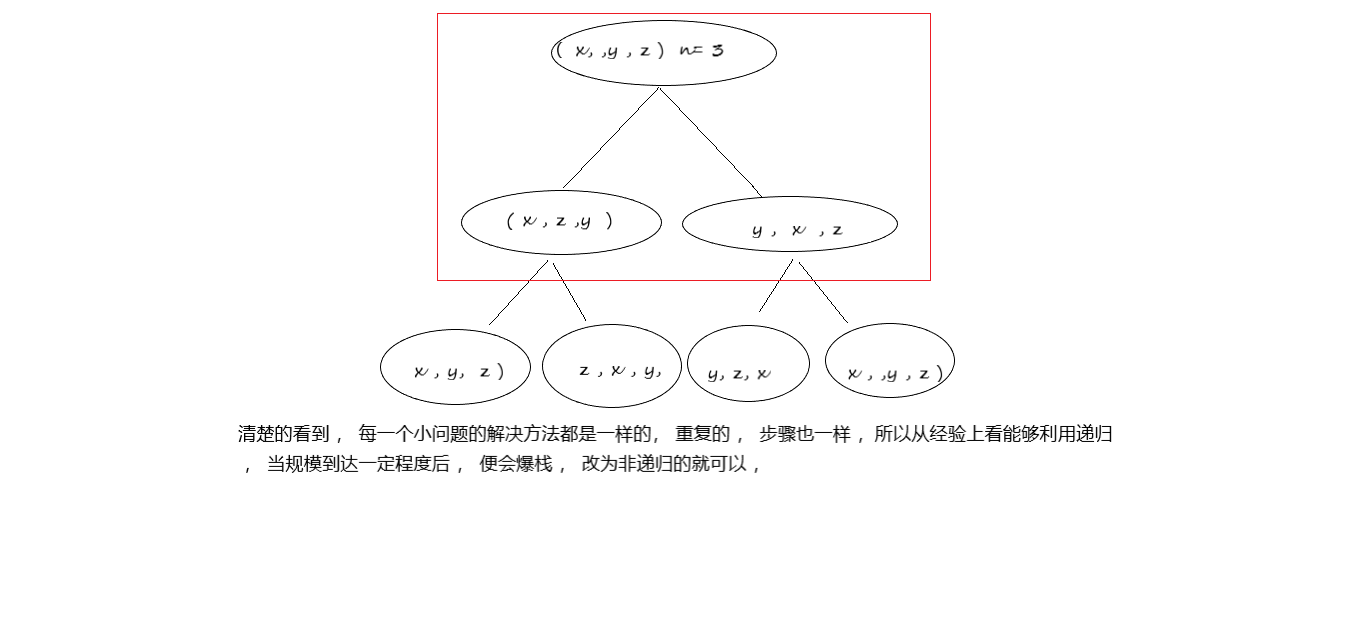
      此时我们似乎也可以发现 ， 双重递归，可以对二叉树经行遍历  。