ABC 042 D - Iroha and a Grid

基本题意

给定一个矩阵，H行W列，左下角的A行B列不可抵达，问从(1, 1)到(H, W)共有多少种路线可以走。

预备知识

乘法原理和加法原理

以本题为例介绍乘法原理。
一件事，分N步完成，每步有ai种走法，那么整件事共有\(a1*a2*...*an\)种完成的方式。
一件事，有N种完成方式，每种完成方式有bi种可能，那么整件事共有\(b1+b2+...+bn\)种完成方式。

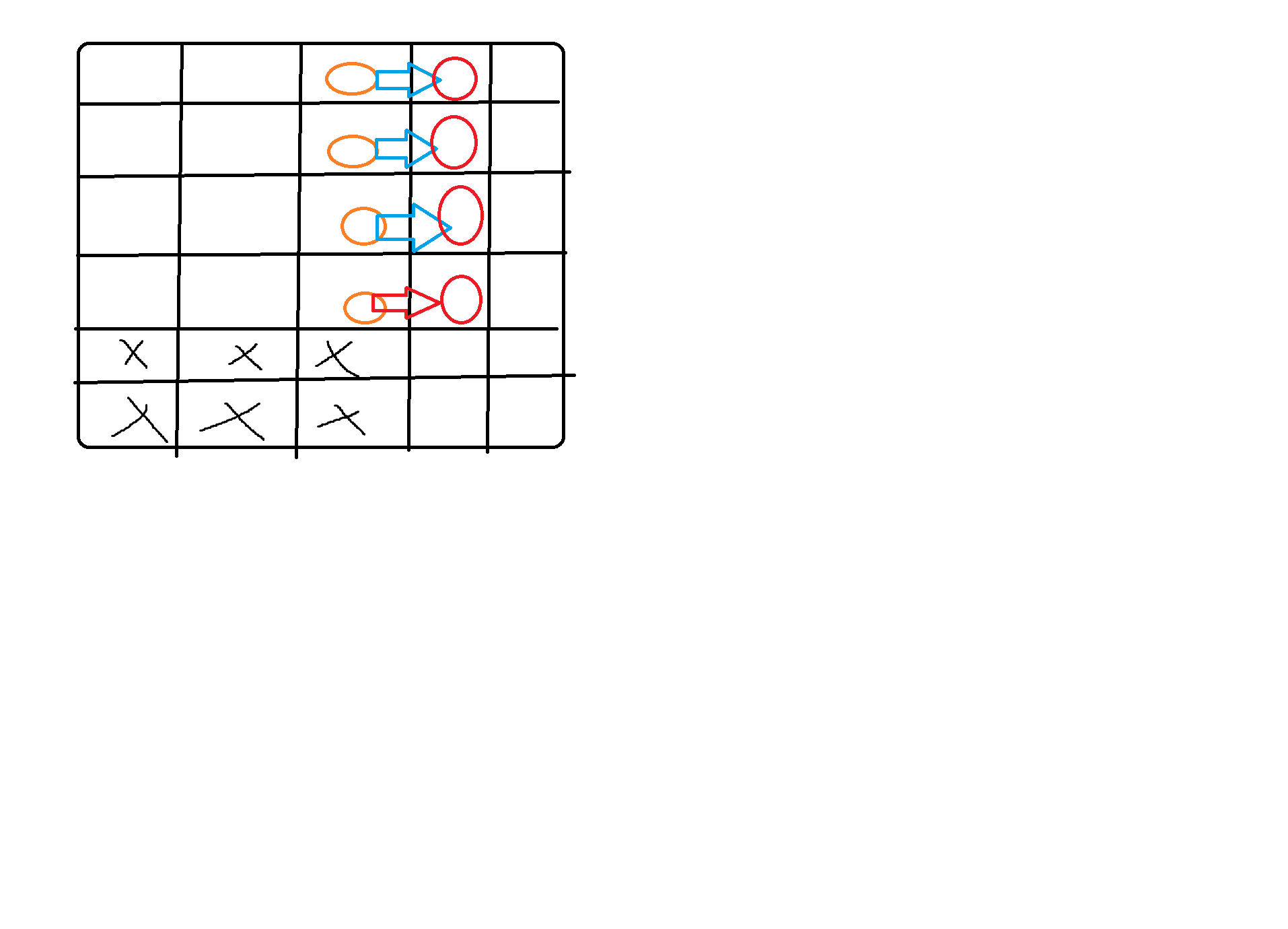
如图，本题中的完成方式可以看作是先走到橙色的方格再走到临接的红色方格。

q1. 每个橙色方格之间冲突吗？
答：不冲突。抵达不同方格是不同的事件。
q2. 为什么只走到临接的红色方格，不走到其他的方格？
答：
从两个方面考虑，第一，已经抵达红色方格后目标不会再向上和向左移动，这是不合法的；
第二，如果向下移动，这种情况再抵达下面的方格的情况中已经被计算过了。

于是我们计算出抵达每个橙色方格，以及从橙色方格邻接的红色方格出发抵达终点的方案数，相乘就得到了结果。

方案数可以用dp求出，但本题数据量过大空间开不下，可以考虑将问题转化如下：
例如从(1, 1)走到(n, m)，可以看作是总共要走n-1+m-1步，在里面挑选了n-1步走纵向，或是挑选了m-1步走横向，得到的结果就是最终答案了。

模意义下的乘法逆元

首先证明模运算对于加法、减法、乘法是可分配的。

1. 加法
   以下论证假设在模k意义下。容易知道任意自然数可以表达成pk+t的形式。
   于是设a = pk+t, b = qk+r。
   (a+b) % k = (p+q)k + (t + r) % k;
   而(a%k) + (b%k) % k = (t + r) % k。
2. 减法
   减法的论证与加法完全类似。
3. 乘法
   (a*b%k) = (pk+t)(qk+r)%k = (pqk^2 + prk + qtk + rt) % k = rt%k;
   (a%k * b%k) % k = rt % k. 得证。
4. 除法
   容易举出反例，如12/3 % 7.

逆元的两种求法

什么是逆元

容易知道模意义下的除法构成了一个独异点，即封闭、可结合、有幺元，但不是每一个元素都有逆元。容易发现，零元是没有逆元的。
模意义下的某一元素\(a\)，如果可以找到另一个\(a^{-1}\)，使得\(a \times a^{-1} \equiv 1 \mod c\)，我们说这个元素\(a\)存在逆元。
这里与正常的除法有些类似，比如我们知道\(3 = (1/3)^{-1}\)，那么18 / 3 就可以用18*((1/3))代换，而逆元利用的是\(x \times x^{-1} = e\)

乘法逆元的唯一性

进行简略的证明。这里的乘号是运算符。
\(设元素a具有逆元b与c， b \neq c。\)
\(容易得到，a = a (恒等式)\)
\(由于a \times b = e, a \times c = e, 有 a \times b = a \times c。\)
\(两侧同乘一个b，有 b \times a \times b = b \times a \times c。\)
\(由b是a的逆元，即得 b = c。\)
\(这与b \neq c 矛盾。\)
\(于是对于一个独异点中的元素，如果它存在逆元，逆元必唯一。\)

任意非零元元素都有逆元

\(设模p意义下的运算。\)
\(运算的二元组每一元必定取自(0, 1, 2, 3, ..., p-1)。\)
\(首先当x = 0时，0是不存在逆元的。\)
\(对于x \neq 0时，设取的元素是a。\)
\(设m, r属于(1, 2, ..., a-1, a+1, ... p-1)，我们假设m, r, m \neq r, 使得m \times a \equiv r \times a \mod p。\)
\(即得\)
\(m \times a = k_1 * p + r_1 , r \times a = k_2 * p + r_2\)
\(由于r_1 = r_2，容易得到(m-r)\times a = (k_1 - k_2) \times p\)
\(k_1 - k_2一定是一个整数，于是就有p | (m - r)。\)
\(但由于m, r均属于1到p-1, 由线性规划易得 |m-r| <= p-2.\)
\(无论m, r, a是怎么样的取值，|m-r|都小于p，不可能整除p；而m-r等于0时与假设不符，得证，即\)
\(在取模意义下的乘法中，任意非零元元素是具有逆元的。\)

乘的逆元等于逆元的乘

\(由于a \times b \times b^{-1} \times a^{-1} = e\)
\(得到(a \times b)^{-1} = b^{-1} \times a^{-1}\)

费马小定理与欧拉函数

\(对于任意互质的a, p，必有a^{p-1} \equiv 1 \mod p\)

证明:

\(设集合(1, 2, 3, 4, 5, 6, ..., p-1)。\)
\(容易发现集合中的数字对p取模会取满集合(1, 2, 3, ..., p-1)。\)
\(再设集合P: (a, 2a, 3a, 4a, ... , (p-1)a)\)
\(证明这样一个性质，P中任取两个元素模p不同余。\)
\(设m \times a \equiv r \times a \mod p, m \neq r\)
\(于是得到m \times a = k_1 * p + r_1 , r \times a = k_2 * p + r_2\)
\(由于r_1 = r_2，容易得到(m-r)\times a = (k_1 - k_2) \times p\)
\(k_1 - k_2一定是一个整数，于是就有p | (m - r)。\)
\(但由于m, r均属于1到p-1, 由线性规划易得 |m-r| <= p-2.\)
\(由于p是质数，那么除了m-r = 0 以外不会有其他情况 p | (m-r)。\)
\(这样证明了P中任取两个元素模p不同余。\)
\(由于任取两个元素模p不同余，并且共有p-1个元素并且任意x属于P不会整除p\)
\(可以得到P中的元素对p取余也是会取满集合(1, 2, 3, ..., p-1)的。\)
\(于是得到等式\)
\(1 \times 2 \times ... \times (p-1) \equiv a \times 2a \times ... \times (p-1)a \mod p\)
\(整理，得到\)
\((p-1)! \equiv a^{p-1} \times (p-1)! \mod p\)
\(由上面论证的性质，任意非零元元素都有逆元，得到\)
\(当p=1时等式显然成立\)
\(当p \neq 1时两侧右乘一个(p-1)!的逆元，得到\)
\(1 \equiv a^{p-1} \mod p\)
\(将右侧拆分，得\)
\(a \times a^{p-2} \equiv 1 \mod p\)
\(即，当a与p互质时，a的乘法逆元是a^{p-2}。\)
\(再由逆元的唯一性，在模p意义下a的乘法逆元唯一。\)

\(费马小定理是欧拉函数在p为质数时的特殊形式。\)

快速幂求逆元

时间复杂度为\(O(lgn)\)。
注意，有，对于mod k意义下，任意的x >= k，x的逆元等于x%k的逆元。

阶乘递推求逆元

\(显然，由于乘法对于模运算的分配性得到\)
\(x! \equiv (x-1)! * x \mod k\)
\(两个非零元相等，那么它们的逆也一定相等（证明略）。结合上面证明的乘的逆元是逆元的乘，得到\)
\((x!)^{-1} \equiv ((x-1)!)^{-1} \times x^{-1}\)
\(容易写出递推式 rev[n] = rev[n-1] * n^{-1}\)

代码

#include <bits/stdc++.h>
// 
#define ios ios::sync_with_stdio(false), cin.tie(0);
#define et cout<<endl;
using namespace std;
typedef pair<int, int> PII;
typedef long long ll;
typedef unsigned long long ull;
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
	while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return x*f;
}
const int N = 2e5+5;
const int M = 2e5+5;
const int mod = 1e9+7;
//
int t, n, k;
ll f[N], rev[N];
ll qmi(ll a, ll k, ll p)
{
	int res = 1;
	while(k)
	{
		if(k&1) res = res * a % p;
		a = (ll) a * a % p;
		k >>= 1;
	}
	return res;
}
void init()
{
	f[0] = 1;
	rev[0] = 1;
	for(int i = 1; i < N; i++)
	{
		f[i] = (ll)f[i-1] * i % mod;
		rev[i] = (ll)rev[i-1] * qmi(i, mod-2, mod) % mod;
	}

}
ll C(int a, int b)
{
	// cout << a << ' ' << b << endl;
	return f[a] * rev[b] % mod * rev[a-b] % mod;
}
int solve()
{
	int H, W, A, B; cin >> H >> W >> A >> B;
	ll res = 0;
	for(int i = 1 ; i <= H - A; i++)
	{
		res = (res + (ll)C(B+i-2, B-1) * C(H-i+W-B-1, W-B-1)) % mod;
		// cout << res << endl;
	}
	cout << res << endl;
	return 0;
}
int main()
{
	ios
	// cin>>t;
	init();
	t = 1;
	while(t--)
	{
		solve();
	}
}