9.30 模拟赛

复盘

T1 不会。

T2 秒了。8:30 写完。

T3 有点感觉。10 点左右会的。12 点写完。卡常了 20 分钟。

T4 不会。

\(10+100+100+20 = 230\)。T1, T4 都是骗分。

总结

好的：

• 切两题。

不足：

• T4 不会。

知识点

• T1：贪心。
• T2：二维偏序。
• T3：前缀和，计数。
• T4：贪心。

题解

A. 网瘾少年

很好很好的贪心题。弱化版是 [CSP-J 2023] 公路，这题没有油箱限制。

首先判掉无解：存在 \(d_i > T\)。

用单调栈求 \(nxt_i\) 表示 \(i\) 之后第一个油价比 \(i\) 低的位置，没有为 \(n + 1\)（终点）。

因为 \(nxt_i\) 的油价比 \(i\) 低，所以你肯定希望先在 \(i\) 买一些油，能够恰好到达 \(nxt_i\)，然后再从 \(nxt_i\) 开始。

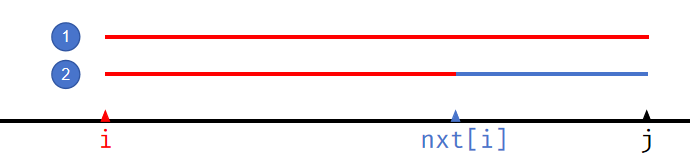
方案一劣于方案二。

反过来说，因为 \(nxt_i\) 是第一个比 \(i\) 便宜的，所以 \([i + 1, nxt_i - 1]\) 内的油价一定比 \(i\) 贵。所以如果我们想到达 \(nxt_i\)，我们会贪心地优先使用 \(i\) 的油，而不是 \([i + 1, nxt_i-1]\) 的题。

但有的时候你只有 \(i\) 的油不能到达 \(nxt_i\)。这时你应该加满，然后到下个加油站贪心。

cin >> n >> T;
for (int i = 1; i <= n; ++ i ) {
	cin >> d[i] >> p[i];
	if (d[i] > T) {
		cout << -1;
		return 0;
	}
	d[i] = d[i - 1] + d[i];
}

stack<int> stk;
stk.push(n + 1);
for (int i = n; i; -- i ) {
	while (stk.size() && p[stk.top()] >= p[i]) stk.pop();
	nxt[i] = stk.top();
	stk.push(i);
}

int e = 0, res = 0;
for (int i = 1; i <= n; ++ i ) {
	int dis = d[nxt[i] - 1] - d[i - 1];
	
	if (e < dis) {
		int t = min(T, dis);
		res += (t - e) * p[i];
		e = t;
	}
	
	e -= d[i] - d[i - 1];
}
cout << res;

B. 宝石之国

设 \(p_i\) 表示 \(i\) 之前第一个和它相同的位置，不存在是 \(0\)。以及权值 \(w_i = i - p_i\)。那么问题变成了求最大的 \(w_i\) 满足：

• \(i \le r\)；
• \(p_i \ge l\)。或者转化成 \(n - p_i \le n - l\)。

这是二维偏序的形式。离线树状数组即可。

C. 网格联通

我场切了，快来膜我。

首先在原图 bfs，给每个点染色。

考虑将 \(k \times k\) 的矩阵炸掉后，哪些连通块会连通。

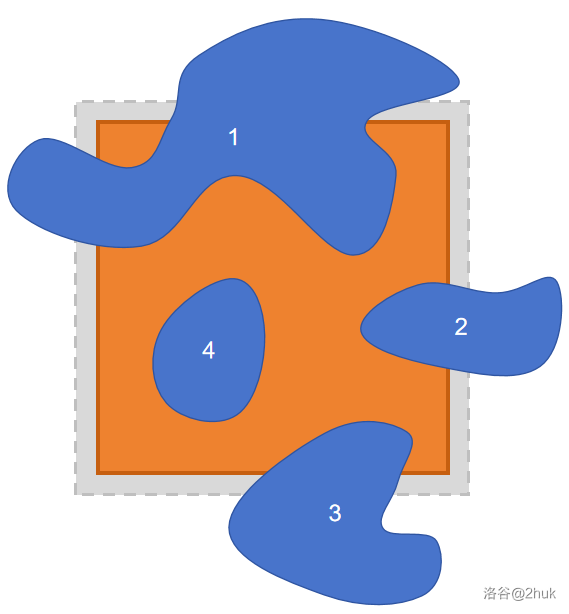
显然这张图中 \(1,2,3,4\) 会联通。而且橙色部分会变成水也连通。

而我们要统计炸掉后，整个连通块的总大小。也就是原来 \(1, 2, 3, 4\) 的大小加上山的数量。

后者可以前缀和简单统计。

对于 \(1, 2, 3\) 的统计是容易。这些连通块与外部接触，我们只需要枚举这个矩阵的外面一圈，也就是灰色一圈。也就是说这种连通块有 \(\mathcal O(k)\) 个。

但是 \(4\) 不好统计，也就是完全不与外界接触（内流水系？）。这种连通块有 \(\mathcal O(k^2)\) 个。

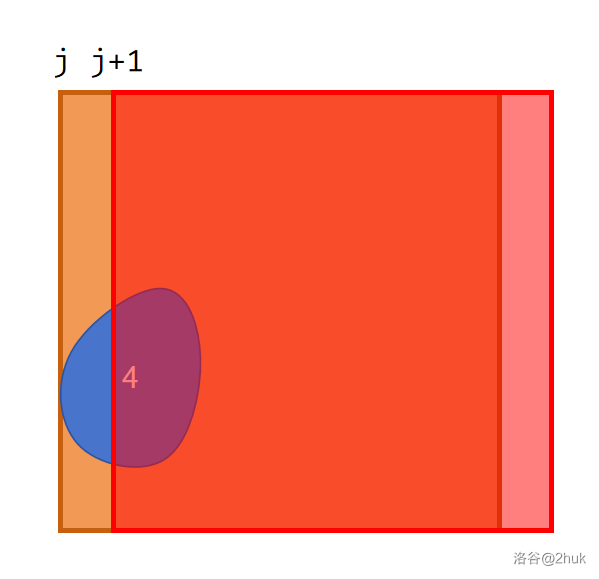
注意到当矩阵的左边界从 \(j\) 移动到 \(j + 1\) 时，至多有 \(\mathcal O(k)\) 个连通块的内流属性发生改变。例如上图 \(4\)。

所以做完了。代码有亿点难写。

D. 星际争霸

先求出 \(a\) 的平均数，然后 \(a \gets a - \bar a\)。现在我们的目标是将所有数变成 \(0\)。

注意到如果我们把隔着 \(k\) 个士兵的一对士兵连边，那么整张图会形成若干个环。我们只需要对于每个环单独考虑。

先考虑链的情况。

• 第一个人想从 \(a_1\) 变成 \(0\)，只能把多的给 \(a_2\)。花费 \(|a_1|\)。

• 第二个人原来 \(a_2\)，但是不得不接受 \(a_1\) 给的 \(a_1\)，也就是 \(a_1 + a_2\)。它只能把多的给 \(a_3\)（给 \(a_1\) 一定不优），花费 \(|a_1+a_2|\)。

• 同理第 \(i\) 个人花费 \(|s_i|\)，其中 \(s_i\) 是 \(a\) 的前缀和。

也就是说总花费是 \(\sum |s_i|\)。

考虑环。可以证明一定存在一对相邻的位置，满足这两个位置没有相互给交换。那么把这个位置剪掉后就是环的问题。

假设断掉了 \([k, k+1]\)。考虑 \(s_i\) 的变化：

• \(k+1\le i \le n\)：\(s_i \gets s_i-s_k\)；
• \(1 \le i \le k\)：\(s_i \gets s_i+s_n-s_k\)。因为 \(s_n = 0\)，所以 \(s_i \gets s_i - s_k\)。

所以总花费是 \(\sum |s_i-s_k|\)。显然这个 \(k\) 取中位数最优。