树做题笔记
\(\color{#3498D8}(1)\) P4281 [AHOI2008] 紧急集合 / 聚会
- 给定一棵 \(n\) 个节点的树。\(m\) 次询问,每次给定 \(a, b, c\),求一个节点 \(u\) 并使得三个点到 \(u\) 的距离和最小。求 \(u\) 和最小距离和。
- \(n, m \le 5 \times 10^5\)。
三个点 \(a, b, c\) 在树上的位置关系一定是这样的(\(a, b, c\) 可以调换):
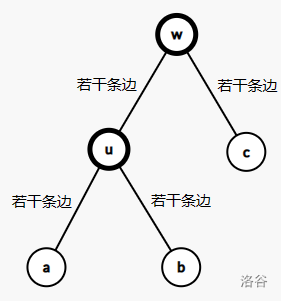
其中”若干条边”可以有 \(0\) 条边。所以这样就包括了所有类似于 \(c\) 是 \(a, b\) 的公共祖先的情况。
可以发现选择 \(u\) 作为中转点一定最优。证明极易,见不会用 printf 打印空格的大佬。
接下来求 \(a, b, c\) 到 \(u\) 的距离和非常简单。一种方法是类似与 LCA 的做法,两个点倍增往上跳。当然也可以利用差分的思想,计算每个点距离根的距离(也就是深度),然后简单容斥计算一下答案为 \(dep_a + dep_b + dep_c - dep_u - 2dep_w\)。
具体的,若令 \(a, b, c\) 任意两点的 LCA 分别为 \(x, y, z\),那么一定会有两个点相同,另一个点不同。那么这个相同的点即 \(w\),不同的点即 \(u\)。
$\color{blue}\text{Code}$
int n, m;
int h[N], e[N], ne[N], idx;
int dep[N];
int fa[N][20];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u, int f) {
dep[u] = dep[f] + 1;
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (f == v) continue;
fa[v][0] = u;
for (int j = 1; j < 20; ++ j )
fa[v][j] = fa[fa[v][j - 1]][j - 1];
dfs(v, u);
}
return;
}
int lca(int a, int b) {
if (dep[a] < dep[b]) swap(a, b);
for (int k = 19; ~k; -- k )
if (dep[fa[a][k]] >= dep[b])
a = fa[a][k];
if (a == b) return a;
for (int k = 19; ~k; -- k )
if (fa[a][k] != fa[b][k])
a = fa[a][k], b = fa[b][k];
return fa[a][0];
}
void Luogu_UID_748509() {
memset(h, -1, sizeof h);
fin >> n >> m;
for (int i = 1; i < n; ++ i ) {
int a, b; fin >> a >> b;
add(a, b), add(b, a);
}
dfs(1, 0);
while (m -- ) {
int a, b, c;
fin >> a >> b >> c;
int pab = lca(a, b);
int pac = lca(a, c);
int pbc = lca(b, c);
int u, w;
if (pab == pac) u = pbc, w = pab;
else if (pab == pbc) u = pac, w = pab;
else u = pab, w = pbc;
fout << u << ' ' << dep[a] + dep[b] + dep[c] - dep[u] - dep[w] * 2 << '\n';
}
}
\(\color{#FFC116}(2)\) P9304 「DTOI-5」3-1
- 给定一棵 \(n\) 个点的树。
你可以花费 \(1\) 个单位时间从某条边的一个端点到达另一个端点。
你总共可以使用一次技能,无论你处于哪个节点,你可以花费 \(0\) 的时间传送到 \(1\) 号节点。
对于所有的 \(k \in [1, n]\),求出从 \(1\) 号点出发并最终返回 \(1\) 号点,经过 \(k\) 个不同的节点,最少需要花费的时间。- \(n \le 10^5\)。
如果没有传送技能,总共要遍历 \(k\) 个点,那么所有的 \(k - 1\) 条边都会被经过两次,则答案为 \(2k - 2\)。
思考传送操作的本质。实际上就是将答案减少了从某个点到 \(1\) 的距离,即某个点的深度减一。我们希望答案尽量小,也就是这个深度尽量大。所以求出所有点的最大深度 \(D\) 即可。
同时,如果 \(k \le D\),那么我们不可能到达深度为 \(D\) 的点,而会到达深度为 \(k + 2\) 的点,所以答案为 \(2k - 2 - (k + 2 - 1) = k - 1\)。
否则答案为 \(2k - 2 - (D - 1)\)。
$\color{blue}\text{Code}$
int n, a, b, c;
vector<int> g[N];
int sz[N], dep[N];
int D;
void dfs(int u, int f) {
sz[u] = 1;
dep[u] = dep[f] + 1;
D = max(D, dep[u]);
for (int v : g[u]) {
if (v != f) {
dfs(v, u);
sz[u] += sz[v];
}
}
return;
}
int res;
void Luogu_UID_748509() {
fin >> n;
for (int i = 1; i <= n; ++ i ) g[i].clear(), sz[i] = dep[i] = 0;
for (int i = 1; i < n; ++ i ) {
fin >> a >> b;
g[a].push_back(b);
g[b].push_back(a);
}
dfs(1, 0);
for (int k = 1; k <= n; ++ k ) {
if (k <= D) fout << k - 1 << '\n';
else fout << 2 * (k - 1) - D + 1 << '\n';
}
return;
}
\(\color{#3498D8}(3)\) CF1806E Tree Master
- 给定一个 \(n\) 个节点的树,每个节点都有权值 \(a_i\)。对于第 \(i(1<i\le n)\) 个节点,有父亲节点 \(p_i\)(规定 \(p_1=0\))。现有两个相同深度的节点 \(x,y\),规定 \(f(x,y)=\begin{cases}0&(x=y=0)\\f(p_x,p_y)+a_x\cdot a_y&(x,y\neq0)\end{cases}\)。\(q\) 次询问求 \(f(x,y)\)。
- \(n, q \le 10^5\)。
记忆化暴力。下面证明为什么复杂度是正确的:
-
转移是 \(\Theta(1)\) 的,所以总复杂度即状态数。若令访问过的深度为 \(i\) 的节点有 \(cnt_i\) 个,那么复杂度即 \(\sum cnt_i^2\)。
-
分类讨论:
- 对于节点数 \(\ge \sqrt n\) 的层,这样的层不会超过 \(\sqrt n\) 个。而每一层最多被访问 \(q\) 次(最坏情况下每次查询都经过这一层),所以复杂度为 \(\Theta(q \sqrt n)\)。
- 对于节点数 $ < \sqrt n$ 的层,假如每层的节点数是 \(x\),那么总共有 \(\frac nx\) 个这样的层。所以状态数为 \(x^2 \times \frac nx = nx\)。因为 \(x < \sqrt n\) 所以复杂度小于 \(\Theta(n \sqrt n)\)。
-
所以复杂度为 \(\Theta((n+q)\sqrt n)\)。
如果用 map/unordered_map 存储记忆化状态会时间/空间会炸。分别考虑两种情况如何解决:
-
对于节点数 \(\ge \sqrt n\) 的层,即使不记忆化复杂度也是 \(\Theta(q \sqrt n)\) 的。所以直接搜索。
-
对于节点数 \(< \sqrt n\) 的层,如果我们令这一层的第 \(idx_y\) 个节点是 \(y\),那么我们可以存储状态 \(f_{x, idx_y}\) 代替 \(f_{x,y }\)。由于 \(idx_y < \sqrt n\),所以用数组存即可。
$\color{blue}\text{Code}$
int n, a[N], p[N], q;
int dep[N], cnt[N];
int f[N][B];
int idx[N];
int sum[N];
int dp(int x, int y) {
if (x == y) return sum[x];
if (cnt[dep[x]] < B) {
if (~f[x][idx[y]]) return f[x][idx[y]];
return f[x][idx[y]] = dp(p[x], p[y]) + a[x] * a[y];
}
return dp(p[x], p[y]) + a[x] * a[y];
}
void Luogu_UID_748509() {
fin >> n >> q;
for (int i = 1; i <= n; ++ i ) fin >> a[i];
for (int i = 2; i <= n; ++ i ) fin >> p[i];
for (int i = 1; i <= n; ++ i ) {
dep[i] = dep[p[i]] + 1;
idx[i] = ++ cnt[dep[i]];
sum[i] = sum[p[i]] + a[i] * a[i];
}
memset(f, -1, sizeof f);
while (q -- ) {
int x, y;
fin >> x >> y;
fout << dp(x, y) << '\n';
}
return;
}
\(\color{#52C41A}(4)\) P8972 『GROI-R1』 一切都已过去
- 给定一颗 \(n\) 个节点的树,边权为实数,点权为整数。\(q\) 给定两个整数 \(x, y\),表示询问树上以 \(x\) 和 \(y\) 为端点的简单路径上边权乘积与点 \(x\) 的点权相乘是否为整数。
- \(n, q \le 2 \times 10^5\),\(a_i \le 10^9\),\(w \le 10^4\),\(w\) 小数位数不超过 \(4\) 位。
若干个数的乘积为整数,可以类似小学乘法。如果这些数的小数位数的和共 \(a\) 位,且将它们的小数点忽略后,乘积末尾有 \(b\) 个 \(0\),那么原数乘积是否为整数等价于是否 \(a \le b\)。
其中求末尾 \(0\) 的个数等价于质因数分解后 \(2, 5\) 中出现次数的较小值。所以我们需要求的是:
- \(x \sim y\) 路径上所有边权小数位数和;
- \(x \sim y\) 路径上所有边权质因数分解后 \(2,5\) 的出现次数;
- \(x\) 质因数分解后 \(2, 5\) 的出现次数。
3rd 极易。如果令 \(f_{0, i}\) 表示根到 \(i\) 节点边权的小数位数的和,\(f_{2,i}\) 表示根到 \(i\) 节点边权的质因数分解后 \(2\) 的出现次数,\(f_{5,i}\) 表示根到 \(i\) 节点边权的质因数分解后 \(5\) 的出现次数。那么 1th 和 2nd 的答案为是 \(f_{0/2/5, x} + f_{0/2/5, y} - 2f_{0/2/5, \operatorname{lca(x, y)}}\)。
注意我们将 \(0\) 看作其中包含 \(\infty\) 个 \(2, 5\)。
$\color{blue}\text{Code}$
int n, q, a[N];
int h[N], e[M], ne[M], idx;
double w[M];
void add(int a, int b, double c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++ ;
}
int f[6][N];
int dep[N];
int fa[N][20];
int zero[N];
int calc(double w, int op = 0) {
int res = 0;
while (w != (int)w) {
++ res;
w *= 10;
}
if (!op) return res;
res = 0; int v = w;
if (!v) return 1e12;
while (v % op == 0) {
++ res;
v /= op;
}
return res;
}
void dfs(int u, int F) {
dep[u] = dep[F] + 1;
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (v == F) continue;
fa[v][0] = u;
for (int j = 1; j < 20; ++ j )
fa[v][j] = fa[fa[v][j - 1]][j - 1];
f[0][v] = f[0][u] + calc(w[i]);
f[2][v] = f[2][u] + calc(w[i], 2);
f[5][v] = f[5][u] + calc(w[i], 5);
zero[v] = zero[u] + (w[i] == 0);
dfs(v, u);
}
return;
}
int lca(int a, int b) {
if (dep[a] < dep[b]) swap(a, b);
for (int i = 19; ~i; -- i )
if (dep[fa[a][i]] >= dep[b])
a = fa[a][i];
if (a == b) return a;
for (int i = 19; ~i; -- i )
if (fa[a][i] != fa[b][i])
a = fa[a][i], b = fa[b][i];
return fa[a][0];
}
void Luogu_UID_748509() {
memset(h, -1, sizeof h);
fin >> n >> q;
for (int i = 1; i <= n; ++ i ) fin >> a[i];
for (int i = 1; i < n; ++ i ) {
int x, y; double z;
scanf("%lld%lld%lf", &x, &y, &z);
add(x, y, z), add(y, x, z);
}
dfs(1, 0);
while (q -- ) {
int x, y; fin >> x >> y;
int p = lca(x, y);
int ten = min(f[2][x] + f[2][y] - 2 * f[2][p] + calc(a[x], 2), f[5][x] + f[5][y] - 2 * f[5][p] + calc(a[x], 5));
int dot = f[0][x] + f[0][y] - 2 * f[0][p];
puts(ten >= dot ? "Yes" : "No");
}
}
\(\color{#3498D8} \text{(5)}\) P5903 【模板】树上 K 级祖先
- 给定一颗 \(n\) 个节点的树,\(q\) 次查询 \(x\) 的 \(k\) 级祖先。
- \(n \le 5 \times 10^5\),\(q \le 5 \times 10^6\)。
如果令 \(x\) 的深度为 \(dep_x\),那么 \(x\) 的 \(k\) 级祖先相当于 \(x\) 的深度为 \(dep_x - k\) 的祖先。令 \(dep_x - k = D\)。
首先重链剖分。
注意一条重链上的 dfs 序是连续的。如果当前节点 \(x\) 和它的深度为 \(D\) 的祖先在同一条重链上,那么我们可以通过 dfs 序计算出这个祖先。否则迭代 \(x \gets \text{father}_{\text{top}_x}\)。
int calc(int x, int k) { // x 的深度为 k 的祖先
if (dep[top[x]] > k) return calc(fa[top[x]], k);
return id[dfn[x] - (dep[x] - k)];
}
$\color{blue}\text{Complete Code}$
#include <bits/stdc++.h>
using namespace std;
const int N = 500010, M = N * 2;
int n, q, s, fa[N];
int dep[N], sz[N], top[N], son[N];
int h[N], e[M], ne[M], idx;
int id[N], dfn[N], ix;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs1(int u) {
dep[u] = dep[fa[u]] + 1, sz[u] = 1;
int res = -1;
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
dfs1(v);
sz[u] += sz[v];
if (sz[v] > res) res = sz[v], son[u] = v;
}
return;
}
void dfs2(int u, int f) {
top[u] = f, dfn[u] = ++ ix, id[ix] = u;
if (son[u]) {
dfs2(son[u], f);
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (v != son[u]) dfs2(v, v);
}
}
return;
}
int calc(int x, int k) { // x 的深度为 k 的祖先
if (dep[top[x]] > k) return calc(fa[top[x]], k);
return id[dfn[x] - (dep[x] - k)];
}
unsigned get(unsigned x) {
x ^= x << 13, x ^= x >> 17, x ^= x << 5;
return s = x;
}
signed main() {
memset(h, -1, sizeof h);
scanf("%d%d%d", &n, &q, &s);
int rt = 0;
for (int i = 1; i <= n; ++ i ) {
scanf("%d", &fa[i]);
add(fa[i], i);
if (!fa[i]) rt = i;
}
dfs1(rt), dfs2(rt, 0);
long long res = 0, ans = 0;
for (int i = 1; i <= q; ++ i ) {
int x = (get(s) ^ res) % n + 1, k = (get(s) ^ res) % dep[x];
ans ^= (long long)i * (res = calc(x, dep[x] - k));
}
printf("%lld\n", ans);
return 0;
}
\(\color{#3498D8}(6)\) P8025 [ONTAK2015] Związek Harcerstwa Bajtockiego
- 给定一棵 \(n\) 个点的无根树,相邻的点之间的距离为 \(1\),一开始你位于 \(m\) 点。之后你将依次收到 \(k\) 个指令,每个指令包含两个整数 \(d\) 和 \(t\),你需要沿着最短路在 \(t\) 步之内(包含 \(t\) 步)走到 \(d\) 点,如果不能走到,则停在最后到达的那个点。请在每个指令之后输出你所在的位置。
- \(n, m, k \le 10^6\),\(t \le 10^9\)。
首先判断如果 \(m \to d\) 的路径长度 \(\ge t\),直接走到 \(d\) 即可。
否则,可以发现 \(m \to d\) 的路径可以分为两步:
- \(m \to \operatorname{lca}(m, d)\),设这段路径长度为 \(x\);
- \(\operatorname{lca}(m, d) \to d\);
我们可以轻易地判断出,如果 \(x \ge t\),那么最终走到的位置属于第一条路径,否则属于第二条路径。
如果最终走到了第一条路径,那么相当于从 \(m\) 往上走 \(t\) 步,即 \(m\) 的 \(t\) 级祖先。同理,如果最终走到了第二条路径,那么相当于先走了 \(\operatorname{dis}(m, d)\) 到达 \(d\) 后,又回退了 \(\operatorname{dis}(m, d) - t\) 步,即 \(d\) 的 \(\operatorname{dis}(m, d) - t\) 级祖先。
求 \(x\) 的 \(k\) 级祖先用上题的模板即可。求 \(\operatorname{dis}(x, y)\) 可以用 \(\operatorname{depth}_a + \operatorname{depth}_b - 2 \cdot \operatorname{depth}_{\operatorname{lca}(x, y)}\) 求出。
$\color{blue}\text{Code}$
int n, m, k, x, y, d, t;
int h[N], e[M], ne[M], idx;
int q, s, fa[N];
int dep[N], sz[N], top[N], son[N];
int id[N], dfn[N], ix;
void dfs1(int u, int f) {
dep[u] = dep[f] + 1, sz[u] = 1;
fa[u] = f;
int res = -1;
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (v == f) continue;
dfs1(v, u);
sz[u] += sz[v];
if (sz[v] > res) res = sz[v], son[u] = v;
}
return;
}
void dfs2(int u, int f) {
top[u] = f, dfn[u] = ++ ix, id[ix] = u;
if (son[u]) {
dfs2(son[u], f);
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (v != fa[u] && v != son[u]) dfs2(v, v);
}
}
return;
}
int calc(int x, int k) { // x 的深度为 k 的祖先
k = dep[x] - k;
while (dep[top[x]] > k) x = fa[top[x]];
return id[dfn[x] - (dep[x] - k)];
}
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
int lca(int a, int b) {
while (top[a] != top[b]) {
if (dep[top[a]] > dep[top[b]]) a = fa[top[a]];
else b = fa[top[b]];
}
return dep[a] < dep[b] ? a : b;
}
void Luogu_UID_748509() {
memset(h, -1, sizeof h);
fin >> n >> m >> k;
for (int i = 1; i < n; ++ i ) {
fin >> x >> y;
add(x, y), add(y, x);
}
dfs1(1, 0), dfs2(1, 0);
while (k -- ) {
fin >> d >> t;
int p = lca(m, d);
if (dep[m] + dep[d] - 2 * dep[p] <= t) m = d;
else if (dep[m] - dep[p] >= t) m = calc(m, t);
else m = calc(d, dep[m] + dep[d] - 2 * dep[p] - t);
fout << m << ' ';
}
return;
}
\(\color{#BFBFBF}(7)\) UOJ387 To Do Tree
有 \(n\) 个任务,做第 \(i\) 个任务需要先做第 \(f_i\) 个任务。依赖关系形成了一棵树,树根为任务 \(1\)。每天你可以完成 \(m\) 个任务,这 \(m\) 个任务之间不能有依赖关系。求最少的完成所有任务的天数。
\(n \le 10^5\)。
贪心策略是每次找子树最大的任务做。
实现上维护一个堆,存储当前哪些任务可以做但还没做,按照子树大小从大到小排序。每次取堆中前 \(m\) 大即可。
$\color{blue}\text{Code}$
struct Tree {
vector<int> g[N];
void add(int a, int b) { g[a].push_back(b); }
vector<int> operator [](const int &u) const { return g[u]; }
}T;
int n, m, fa[N], sz[N];
void Luogu_UID_748509() {
fin >> n >> m;
fill(sz + 1, sz + n + 1, 1);
for (int i = 2; i <= n; ++ i ) {
fin >> fa[i];
T.add(fa[i], i);
}
for (int i = n; i >= 2; -- i ) {
sz[fa[i]] += sz[i];
}
priority_queue<PII> q;
q.emplace(sz[1], 1);
int tmp = 0;
vector<vector<int> > ans;
while (tmp < n) {
vector<int> vec;
for (int i = 1; i <= m && q.size(); ++ i ) {
vec.emplace_back(q.top().second);
q.pop();
++ tmp;
}
ans.emplace_back(vec);
for (int u : vec) {
for (int v : T[u]) {
q.emplace(sz[v], v);
}
}
}
fout << ans.size() << '\n';
for (vector<int> t : ans) {
fout << t.size() << ' ' << t;
}
}
\(\color{#9D3DCF}(8)\) P4211 [LNOI2014] LCA
- 给定一颗 \(n\) 的节点的树。\(m\) 次询问 \(\sum_{i=l}^r \operatorname{depth}_{\operatorname{lca}(i, z)}\)。
- \(n, m \le 5 \times 10^4\)。
考虑几个弱化版本:
- \(m\) 次询问 \(\operatorname{depth}_{\operatorname{lca}(x, y)}\)。
显然可以用朴素做法。这里的做法是这样的:
- 将 \(x\) 到根上每个点加 \(1\),那么 \(y\) 到根的点权和即答案。原因是 \(x, y\) 到根的公共路径长度就是它们最近公共祖先的深度。
- 实现用树剖解决。
$\color{blue}\text{Code}$
while (m -- ) {
int x, y;
scanf("%d%d", &x, &y);
modify(1, x, 1); // 1 到 x 的路径加一
printf("%d\n", query(1, y)); // 1 到 y 的路径和
modify(1, x, -1); // 清空
}
- 单次询问 \(\sum_{i=l}^r \operatorname{depth}_{\operatorname{lca}(i, z)}\)。
显然也可以用朴素做法。这里我们延续上一问的做法:
- 对于所有 \(i \in [l, r]\),将 \(i\) 到根上每个点累加 \(1\),那么 \(z\) 到根的点权和即答案。
$\color{blue}\text{Code}$
int l, r, z;
scanf("%d%d%d", &l, &r, &z);
for (int i = l; i <= r; ++ i ) modify(1, i, 1); // 1 到 i 的路径加一
printf("%d\n", query(1, z)); // 1 到 z 的路径和
- \(m\) 次询问 \(\sum_{i=\color{red}\mathbf1}^r \operatorname{depth}_{\operatorname{lca}(i, z)}\)。
显然不能用朴素做法了。做法是这样的:
- 考虑离线所有询问。vector 以 \(r\) 做下标,存储每个询问的编号和 \(z\)。即
vec[r].push_back(make_pair(i, z))。 - 枚举 \(i = (1, 2, \dots, n)\),并每次将 \(i\) 到根上每个点累加 \(1\)。
- 然后访问 vector 的 \(i\) 中的所有元素 \((j, z)\),我们将 \(z\) 到根的点权和累加到询问 \(j\) 的答案中。
$\color{blue}\text{Code}$
int res[N]; // 第 i 问的答案
vector<pair<int, int> > vec[N];
for (int i = 1; i <= m; ++ i ) {
scanf("%d%d", &a[i].r, &a[i].z);
vec[a[i].r].push_back({i, a[i].z});
}
for (int i = 1; i <= n; ++ i ) {
modify(1, i, 1); // 1 到 i 的路径加一
for (pair<int, int> t : vec[i]) {
int a = t.first, b = t.second;
res[a] += query(1, b); // 1 到 i 的路径和
}
}
for (int i = 1; i <= n; ++ i ) printf("%d\n", res[i]);
- \(m\) 次询问 \(\sum_{i=l}^r \operatorname{depth}_{\operatorname{lca}(i, z)}\),即本题。
上一问差分即可。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 50010, M = N << 1;
int n, m, fa[N];
int h[N], e[M], ne[M], idx;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
vector<pair<int, int> > vec[N];
int res[N];
int dep[N], top[N], son[N], id[N], cnt, sz[N];
void dfs1(int u) {
dep[u] = dep[fa[u]] + 1;
sz[u] = 1;
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
dfs1(v);
sz[u] += sz[v];
if (sz[u] > sz[son[u]]) son[u] = v;
}
}
void dfs2(int u, int t) {
top[u] = t;
id[u] = ++ cnt;
if (son[u]) {
dfs2(son[u], t);
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (v != son[u]) dfs2(v, v);
}
}
}
struct Tree {
int l, r, v, tag;
}tr[N << 2];
void pushup(int u) {
tr[u].v = tr[u << 1].v + tr[u << 1 | 1].v;
}
void calc(int u, int k) {
tr[u].tag += k;
tr[u].v += k * (tr[u].r - tr[u].l + 1);
}
void pushdown(int u) {
calc(u << 1, tr[u].tag), calc(u << 1 | 1, tr[u].tag);
tr[u].tag = 0;
}
void build(int u, int l, int r) {
tr[u] = {l, r, 0, 0};
if (l != r) {
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}
}
void modify(int u, int l, int r) {
if (tr[u].l >= l && tr[u].r <= r) calc(u, 1);
else {
int mid = tr[u].l + tr[u].r >> 1;
pushdown(u);
if (l <= mid) modify(u << 1, l, r);
if (r > mid) modify(u << 1 | 1, l, r);
pushup(u);
}
}
int query(int u, int l, int r) {
if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;
int res = 0, mid = tr[u].l + tr[u].r >> 1;
pushdown(u);
if (l <= mid) res = query(u << 1, l, r);
if (r > mid) res += query(u << 1 | 1, l, r);
return res;
}
void Tree_modify(int a, int b) {
while (top[a] != top[b]) {
if (dep[top[a]] < dep[top[b]]) swap(a, b);
modify(1, id[top[a]], id[a]);
a = fa[top[a]];
}
if (dep[a] > dep[b]) swap(a, b);
modify(1, id[a], id[b]);
}
int Tree_query(int a, int b) {
int res = 0;
while (top[a] != top[b]) {
if (dep[top[a]] < dep[top[b]]) swap(a, b);
res += query(1, id[top[a]], id[a]);
a = fa[top[a]];
}
if (dep[a] > dep[b]) swap(a, b);
return res + query(1, id[a], id[b]);
}
signed main() {
memset(h, -1, sizeof h);
scanf("%lld%lld", &n, &m);
for (int i = 2; i <= n; ++ i ) {
scanf("%lld", fa + i);
fa[i] ++ ;
add(fa[i], i);
}
for (int i = 1; i <= m; ++ i ) {
int l, r, z;
scanf("%lld%lld%lld", &l, &r, &z);
vec[1 + r].push_back({i, 1 + z});
vec[l].push_back({-i, 1 + z});
}
dfs1(1), dfs2(1, 0);
build(1, 1, n);
for (int i = 1; i <= n; ++ i ) {
Tree_modify(1, i);
for (pair<int, int> t : vec[i]) {
int a = abs(t.first), b = t.second;
int k = t.first > 0 ? 1 : -1;
res[a] += k * Tree_query(1, b);
}
}
for (int i = 1; i <= m; ++ i ) printf("%lld\n", res[i] % 201314);
return 0;
}
\(\color{#9D3DCF}(9)\) P2680 [NOIP2015 提高组] 运输计划
- 给定一棵 \(n\) 个点的树,边有边权 \(w_i\)。给定 \(m\) 条路径 \((u_i,v_i)\)。你可以选择一条边,将其边权变为 \(0\)。最小化这 \(m\) 条路径长度的最大值。
- \(n, m \le 3 \times 10^5\)。
二分答案 \(mid\)。
对于原来路径长度 \(\le mid\),我们无需考虑。换句话说,我们需要考虑的是长度 \(> mid\) 的路径。
对于这些路径而言,我们希望通过仅改变树上一条边,让这些路径的长度都变得 \(\le mid\)。显然这条边需要是这些路径的交,而且是交中边权最大的。
找路径交可以用树上差分的套路。
找到这条设为 \(0\) 的边后简单判断一下即可。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
using namespace std;
const int N = 300010, M = N * 2, K = 19;
int n, m;
int h[N], e[M], ne[M], idx, w[M];
int fa[N][K], dep[N], dis[N];
int seq[N], cnt;
struct Path
{
int a, b, p, d;
}q[N];
void add(int a, int b, int c)
{
e[idx] = b, ne[idx] = h[a], w[idx] =c, h[a] = idx ++ ;
}
void dfs(int u, int F, int D)
{
seq[cnt ++ ] = u;
dep[u] = D;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j == F) continue;
fa[j][0] = u;
for (int k = 1; k < K; ++ k )
fa[j][k] = fa[fa[j][k - 1]][k - 1];
dis[j] = dis[u] + w[i];
dfs(j, u, D + 1);
}
}
int lca(int a, int b)
{
if (dep[a] < dep[b]) swap(a, b);
for (int k = K - 1; ~k; -- k )
if (dep[fa[a][k]] >= dep[b])
a = fa[a][k];
if (a == b) return a;
for (int k = K - 1; ~k; -- k )
if (fa[a][k] != fa[b][k])
a = fa[a][k], b = fa[b][k];
return fa[a][0];
}
int sum[N];
bool chk(int mid)
{
memset(sum, 0, sizeof sum);
int c = 0, mx = 0;
for (int i = 0; i < m; ++ i )
{
int a = q[i].a, b = q[i].b, p = q[i].p, d = q[i].d;
if (d > mid)
{
++ c;
mx = max(mx, d);
++ sum[a], ++ sum[b], sum[p] -= 2;
}
}
if (!c) return true;
for (int i = n - 1; ~i; -- i )
{
int j = seq[i];
sum[fa[j][0]] += sum[j];
}
for (int i = 1; i <= n; ++ i )
if (sum[i] == c && mx - dis[i] + dis[fa[i][0]] <= mid)
return true;
return false;
}
int main()
{
memset(h, -1, sizeof h);
cin >> n >> m;
for (int i = 1; i < n; ++ i )
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
dfs(1, -1, 1);
for (int i = 0; i < m; ++ i )
{
int a, b;
cin >> a >> b;
int p = lca(a, b);
int d = dis[a] + dis[b] - dis[p] * 2;
q[i] = {a, b, p, d};
}
int l = 0, r = 3e8;
while (l < r)
{
int mid = l + r >> 1;
if (chk(mid)) r = mid;
else l = mid + 1;
}
cout << l;
return 0;
}
\(\color{#9D3DCF}(10)\) P2486 [SDOI2011] 染色
- 给定一棵 \(n\) 个点的树,每个点上有一个颜色。你需要支持两种操作:
- 将一条链 \((x,y)\) 上的点全部染成颜色 \(c\)。
- 询问一条链 \((x,y)\) 上的点的颜色组成了几个颜色段。
- \(n \le 10^5\)。
树剖套线段树。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
const int N = 100010;
int n, m, w[N];
int id[N], idx, pos[N];
struct Node {
int l, r;
int v, tag, L, R;
}tr[N << 2];
Node operator +(Node a, Node b) {
Node res;
res.L = a.L;
res.R = b.R;
res.v = a.v + b.v - (a.R == b.L);
return res;
}
struct Segment_Tree {
void pushup(int u) {
tr[u].L = tr[u << 1].L;
tr[u].R = tr[u << 1 | 1].R;
tr[u].v = tr[u << 1].v + tr[u << 1 | 1].v - (tr[u << 1].R == tr[u << 1 | 1].L);
}
void build(int u, int l, int r) {
tr[u] = {l, r, 0, -1, 0, 0};
if (l == r) tr[u].L = tr[u].R = w[pos[l]], tr[u].v = 1;
else {
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
pushup(u);
}
}
void calc(int u, int c) {
tr[u].L = tr[u].R = tr[u].tag = c;
tr[u].v = 1;
}
void pushdown(int u) {
if (~tr[u].tag) calc(u << 1, tr[u].tag), calc(u << 1 | 1, tr[u].tag);
tr[u].tag = -1;
}
void modify(int u, int l, int r, int c) {
if (tr[u].l >= l && tr[u].r <= r) calc(u, c);
else {
int mid = tr[u].l + tr[u].r >> 1;
pushdown(u);
if (l <= mid) modify(u << 1, l, r, c);
if (r > mid) modify(u << 1 | 1, l, r, c);
pushup(u);
}
}
Node query(int u, int l, int r) {
if (tr[u].l >= l && tr[u].r <= r) return tr[u];
int mid = tr[u].l + tr[u].r >> 1;
pushdown(u);
if (l <= mid && r > mid) return query(u << 1, l, r) + query(u << 1 | 1, l, r);
if (l <= mid) return query(u << 1, l, r);
return query(u << 1 | 1, l, r);
}
int query(int u, int x) {
if (tr[u].l == tr[u].r) return tr[u].L;
int mid = tr[u].l + tr[u].r >> 1;
pushdown(u);
if (x <= mid) return query(u << 1, x);
return query(u << 1 | 1, x);
}
}S;
struct Tree {
std::vector<int> g[N];
int fa[N], dep[N], sz[N], son[N], top[N];
void add(int a, int b) { g[a].push_back(b); }
std::vector<int> operator [](const int &u) const { return g[u]; }
void dfs1(int u, int f) {
fa[u] = f;
dep[u] = dep[f] + 1;
sz[u] = 1;
for (int v : g[u]) {
if (v == f) continue;
dfs1(v, u);
sz[u] += sz[v];
if (sz[v] > sz[son[u]]) son[u] = v;
}
}
void dfs2(int u, int f) {
top[u] = f;
id[u] = ++ idx;
pos[idx] = u;
if (son[u]) {
dfs2(son[u], f);
for (int v : g[u])
if (v != fa[u] && v != son[u])
dfs2(v, v);
}
}
int query(int a, int b) {
int res = 0;
while (top[a] != top[b]) {
if (dep[top[a]] < dep[top[b]]) std::swap(a, b);
res += S.query(1, id[top[a]], id[a]).v - (S.query(1, id[fa[top[a]]]) == S.query(1, id[top[a]]));
a = fa[top[a]];
}
if (dep[a] > dep[b]) std::swap(a, b);
return res + S.query(1, id[a], id[b]).v;
}
void modify(int a, int b, int c) {
while (top[a] != top[b]) {
if (dep[top[a]] < dep[top[b]]) std::swap(a, b);
S.modify(1, id[top[a]], id[a], c);
a = fa[top[a]];
}
if (dep[a] > dep[b]) std::swap(a, b);
S.modify(1, id[a], id[b], c);
}
}T;
int main() {
std::cin >> n >> m;
for (int i = 1; i <= n; ++ i ) std::cin >> w[i];
for (int i = 1, u, v; i < n; ++ i ) {
std::cin >> u >> v;
T.add(u, v), T.add(v, u);
}
T.dfs1(1, 0), T.dfs2(1, 0);
S.build(1, 1, n);
while (m -- ) {
char op;
int a, b, c;
std::cin >> op >> a >> b;
if (op == 'Q') std::cout << T.query(a, b) << '\n';
else {
std::cin >> c;
T.modify(a, b, c);
}
}
return 0;
}
\(\color{#9D3DCF}(11)\) P5478 [BJOI2015] 骑士的旅行
- 给定一颗 \(n\) 个节点的树。有 \(m\) 个骑士,最开始第 \(i\) 个骑士在 \(p_i\) 节点上,武力值为 \(f_i\)。接下来有 \(q\) 次操作 \((t_i, x_i, y_i)\):
- \(t_i = 1\),输出树上 \(x_i, y_i\) 路径上的前 \(k\) 大骑士的武力值。
- \(t_i = 2\),\(p_{x_i} \gets y_i\);
- \(t_i = 3\),\(f_{x_i} \gets y_i\)。
- \(n, m \le 4 \times 10^4\),\(q \le 8 \times 10^4\),\(\color{red}k \le 20\)。
显然需要树链剖分,将树上问题转化成序列上问题。
发现 \(k\) 很小,所以我们可以用线段树维护前 \(k\) 大,并用 \(\mathcal O(k)\) 的时间复杂度 pushup。
注意可用 multiset 存储每个叶子节点上的骑士编号和骑士武力值。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 800010;
int n, m, f[N], p[N], q, k;
int id[N], idx, pos[N];
vector<int> vec[N];
vector<int> calc(vector<int> t) {
vector<int> res;
sort(t.begin(), t.end(), greater<int>());
for (int i = 0; i < t.size() && i < k; ++ i ) res.push_back(t[i]);
return res;
}
struct Node {
int l, r;
vector<int> V;
multiset<int, greater<int> > S;
}tr[N << 2];
struct Segment_Tree {
void pushup(int u) {
vector<int> res;
for (int t : tr[u << 1].V) res.push_back(t);
for (int t : tr[u << 1 | 1].V) res.push_back(t);
tr[u].V = calc(res);
}
void build(int u, int l, int r) {
tr[u].l = l, tr[u].r = r;
if (l == r) {
l = pos[l];
for (int i = 0; i < vec[l].size(); ++ i ) {
tr[u].S.insert(vec[l][i]);
tr[u].V.push_back(vec[l][i]);
}
tr[u].V = calc(tr[u].V);
}
else {
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
pushup(u);
}
}
void modify(int u, int x, int d) {
if (tr[u].l == tr[u].r) {
if (d > 0) tr[u].S.insert(d);
else {
tr[u].S.erase(tr[u].S.find(-d));
}
int cnt = 0;
tr[u].V.clear();
for (int t : tr[u].S) {
++ cnt;
if (cnt > k) break;
tr[u].V.push_back(t);
}
}
else {
int mid = tr[u].l + tr[u].r >> 1;
if (x <= mid) modify(u << 1, x, d);
else modify(u << 1 | 1, x, d);
pushup(u);
}
}
vector<int> query(int u, int l, int r) {
if (tr[u].l >= l && tr[u].r <= r) return tr[u].V;
int mid = tr[u].l + tr[u].r >> 1;
vector<int> res;
if (l <= mid) {
for (int t : query(u << 1, l, r)) res.push_back(t);
}
if (r > mid) {
for (int t : query(u << 1 | 1, l, r)) res.push_back(t);
}
return calc(res);
}
}S;
struct Tree {
vector<int> g[N];
void add(int a, int b) { g[a].push_back(b); }
int fa[N], dep[N], sz[N], son[N], top[N];
void dfs1(int u, int f) {
fa[u] = f;
dep[u] = dep[f] + 1;
sz[u] = 1;
for (int v : g[u]) {
if (v == f) continue;
dfs1(v, u);
sz[u] += sz[v];
if (sz[v] > sz[son[u]]) son[u] = v;
}
}
void dfs2(int u, int f) {
top[u] = f;
id[u] = ++ idx;
pos[idx] = u;
if (son[u]) {
dfs2(son[u], f);
for (int v : g[u])
if (v != fa[u] && v != son[u])
dfs2(v, v);
}
}
vector<int> query(int a, int b) {
vector<int> res;
while (top[a] != top[b]) {
if (dep[top[a]] < dep[top[b]]) swap(a, b);
for (int t : S.query(1, id[top[a]], id[a])) res.push_back(t);
res = calc(res);
a = fa[top[a]];
}
if (dep[a] > dep[b]) swap(a, b);
for (int t : S.query(1, id[a], id[b])) res.push_back(t);
return calc(res);
}
void modify(int x, int y) {
S.modify(1, id[x], y);
}
}T;
signed main() {
cin >> n;
for (int i = 1, u, v; i < n; ++ i ) {
cin >> u >> v;
T.add(u, v), T.add(v, u);
}
cin >> m;
for (int i = 1; i <= m; ++ i ) {
cin >> f[i] >> p[i];
vec[p[i]].push_back(f[i]);
}
cin >> q >> k;
T.dfs1(1, 0), T.dfs2(1, 0);
S.build(1, 1, n);
while (q -- ) {
int t, x, y;
cin >> t >> x >> y;
if (t == 1) {
auto res = T.query(x, y);
if (res.empty()) cout << "-1\n";
else {
for (int t : res) cout << t << ' ';
cout << '\n';
}
}
else if (t == 2) {
T.modify(p[x], -f[x]);
T.modify(y, f[x]);
p[x] = y;
}
else {
T.modify(p[x], -f[x]);
T.modify(p[x], y);
f[x] = y;
}
}
return 0;
}
\(\color{#3498D8}(12)\) P6374 「StOI-1」树上询问
给定一棵 \(n\) 个点的无根树,有 \(q\) 次询问。
每次询问给一个参数三元组 \((a,b,c)\) ,求有多少个 \(i\) 满足这棵树在以 \(i\) 为根的情况下 \(a\) 和 \(b\) 的 LCA 为 \(c\) 。
\(n \le 5 \times 10^5\),\(q \le 2 \times 10^5\)。
模拟可知答案为当这棵树以 \(c\) 为根时除 \(a, b\) 所在子树内的点的数量,即 \(n - size_a - size_b\)。以及当 \(c\) 不在树上 \(a \sim b\) 的路径上时答案为 \(0\)。
所以我们需要解决两个问题:
-
判断 \(c\) 是否在 \(a \sim b\) 的路径上:
首先求出 \(\operatorname{lca}(a, b) = p\)。那么此时我们需要判断的就是是否 \(c\) 在 \(a \sim p\) 的路径上或 \(b \sim p\) 的路径上。即:
bool chk(int a, int b, int c) { int p = lca(a, b); return (lca(a, c) == c || lca(b, c) == c) && lca(c, p) == p; } -
求当以 \(c\) 为根时,\(a\) 所在子树的大小:
分类讨论:
- 当 \(c\) 原来就是 \(a\) 的祖先时,做法是类似于 lca 的倍增往上跳,跳到某个点使得这个点的父亲是 \(a\);
- 否则,显然整棵树中,除了 \(c\) 所在的子树外,每个点都是 \(a\) 所在的子树,即答案为 \(n - size_c\)。
即:
int F(int a, int b) { for (int k = 19; ~k; -- k ) if (dep[fa[b][k]] > dep[a]) b = fa[b][k]; return b; } int calc(int a, int b) { if (a == b) return 0; if (lca(a, b) == b) return sz[F(b, a)]; return n - sz[b]; }
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
using namespace std;
const int N = 1000010;
int n, q;
vector<int> g[N];
int sz[N], fa[N][20], dep[N];
void dfs(int u, int f) {
dep[u] = dep[f] + 1, sz[u] = 1;
for (int v : g[u])
if (v != f) {
fa[v][0] = u;
for (int k = 1; k < 20; ++ k ) fa[v][k] = fa[fa[v][k - 1]][k - 1];
dfs(v, u);
sz[u] += sz[v];
}
}
int lca(int a, int b) {
if (dep[a] < dep[b]) swap(a, b);
for (int k = 19; ~k; -- k )
if (dep[fa[a][k]] >= dep[b]) a = fa[a][k];
if (a == b) return a;
for (int k = 19; ~k; -- k )
if (fa[a][k] != fa[b][k]) a = fa[a][k], b = fa[b][k];
return fa[a][0];
}
bool chk(int a, int b, int c) {
int p = lca(a, b);
return (lca(a, c) == c || lca(b, c) == c) && lca(c, p) == p;
}
int F(int a, int b) {
for (int k = 19; ~k; -- k )
if (dep[fa[b][k]] > dep[a]) b = fa[b][k];
return b;
}
int calc(int a, int b) {
if (a == b) return 0;
if (lca(a, b) == b) return sz[F(b, a)];
return n - sz[b];
}
int main() {
cin >> n >> q;
for (int i = 1, a, b; i < n; ++ i ) {
cin >> a >> b;
g[a].emplace_back(b);
g[b].emplace_back(a);
}
dfs(1, 0);
while (q -- ) {
int a, b, c;
cin >> a >> b >> c;
int res = 0;
if (!chk(a, b, c)) res = 0;
else res = n - calc(a, c) - calc(b, c);
cout << res << '\n';
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号