数论做题笔记

\(\color{#FFC116}(1)\) P6075 [JSOI2015] 子集选取

• 给定 \(n\) 个元素的集合 \(S = \{1, 2, \dots, n\}\) 和整数 \(k\)。求有多少组 \(\frac 12 k(k+1)\) 个集合 \(A_{i, j}\) 使得 \(A_{i, j} \subseteq S,1 \le j \le i \le k\) 且 \(A_{i, j} \subseteq A_{i, j - 1} \cap A_{i - 1, j}\)。
• \(n, k \le 10^9\)。

首先考虑 \(n = 1\)。那么一定存在某条轮廓线，使得这条轮廓线上的集合均为 \(\{1\}\)，轮廓线下的集合均为 \(\varnothing\)。

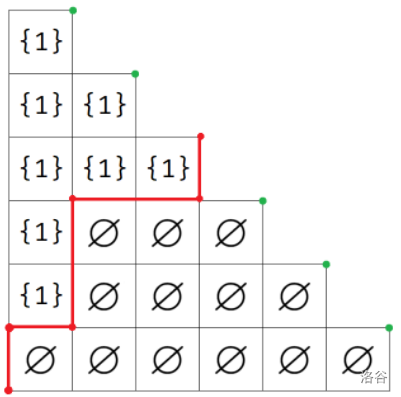
那么答案显然为轮廓线的数量，也即从左下角往右上走，且只能向上或向右，最终到达图中绿点的方案数。总步数为 \(k\)，那么方案数即 \(2^k\)。

考虑更普遍的 \(n > 1\) 的情况。可以发现对于不同的数字是可以分别考虑的，也就是说每个格点中是否包含某个数 \(x\) 的情况所构成的图也是存在这一条轮廓线的。例如 \(n = 3\)：

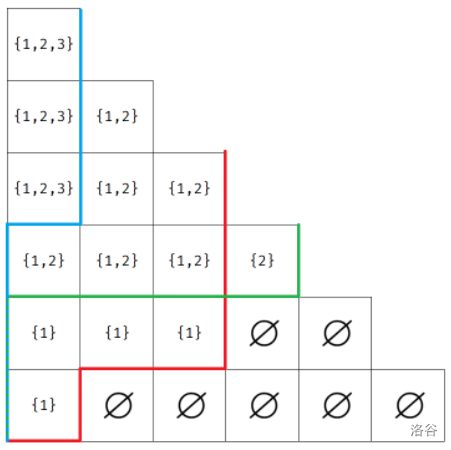
那么答案即为 \((2^k)^n = 2^{kn}\)。

$\color{blue}\text{Code}$

int fpm(int a, int b) {
	int res = 1;
	while (b) {
		if (b & 1) res = (ll)res * a % P;
		b >>= 1, a = (ll)a * a % P;
	}
	return res;
}

void Luogu_UID_748509() {
	int a, b;
	fin >> a >> b;
	fout << fpm(2, a * b) << '\n';
}

\(\color{#51A41C}(2)\) P1072 [NOIP2009 提高组] Hankson 的趣味题

• \(n\) 组询问。每次给定 \(a_0, a_1, b_0, b_1\)，求有多少正整数 \(x\) 使得 \(\gcd(a_0, x) = a_1\) 且 \(\operatorname{lcm}(b_0, x) = b_1\)。
• \(1 \le a_0, a_1, b_0, b_1 \le 2 \times 10^9\)，\(n \le 2 \times 10^3\)。

对于一个质数 \(i\)，我们令 \(f_x(i)\) 表示 \(x\) 分解质因数后 \(i\) 的出现次数。

那么我们可以对于 \(x\) 的每个质因数单独考虑，求出每个质因数的取值方案数，那么所有这些方案数相乘即为最终答案。不妨令我们当前考虑的质数为 \(i\)。

通过 \(\gcd(a_0, x) = a_1\) 可以得知 \(\min(f_{a_0}(i), f_x(i)) = f_{a_1}(i)\)，通过 \(\operatorname{lcm}(b_0, x) = b_1\) 可以得知 \(\max(f_{b_0}(i), f_x(i)) = f_{b_1}(i)\)。其中 \(f_{a_0}(i),f_{a_1}(i),f_{b_0}(i),f_{b_1}(i)\) 都是可以预处理求知的。

此时发现通过这两个条件可以推出两个 \(f_x(i)\) 的取值范围，这两个范围再取交集的长度即这个质因数的方案数。

$\color{blue}\text{Code}$

int a0, a1, b0, b1;
map<int, int> primes[4];
set<int> S;

void init(int x, int id) {
	for (int i = 2; i <= x / i; ++ i )
		if (x % i == 0) {
			S.insert(i);
			while (x % i == 0) {
				++ primes[id][i];
				x /= i;
			}
		}
	
	if (x > 1) {
		S.insert(x);
		++ primes[id][x];
	}
}

struct Range {
	int l, r;
	Range operator +(const Range &h) const {
		return {max(l, h.l), min(r, h.r)};
	}
};

Range calcmin(int a, int b) {
	// min(a, x) == b，x 的范围？
	if (a < b) return {INF, -INF};
	if (a == b) return {a, INF};
	return {b, b};
}

Range calcmax(int a, int b) {
	// max(a, x) == b，x 的范围？
	if (a > b) return {INF, -INF};
	if (a == b) return {-INF, a};
	return {b, b};
}

void Luogu_UID_748509() {
	S.clear();
	for (int i : {0, 1, 2, 3}) primes[i].clear();
	
	fin >> a0 >> a1 >> b0 >> b1;
	init(a0, 0), init(a1, 1), init(b0, 2), init(b1, 3);
	
	int res = 1;
	for (int p : S) {
		auto range = calcmin(primes[0][p], primes[1][p]) + calcmax(primes[2][p], primes[3][p]);
		res *= max(0ll, range.r - range.l + 1);
	}
	
	fout << res << '\n';
	return;
}

\(\color{#9D3DCF}(3)\) P4139 上帝与集合的正确用法

• \(T\) 组询问，给定 \(p\)，求 \(2^{2^{2^{2^{\dots}}}} \bmod p\)。
• \(T \le 10^3\)，\(p \le 10^7\)。

令 \(x = 2^{2^{2^{2^{\dots}}}},f(p) = 2^{2^{2^{\dots}}} \bmod p\)。不难发现 \(x = 2^x\)，所求为 \(f(p)\)。

根据扩展欧拉定理可得：

\[2^x\equiv\left\{\begin{matrix}2^x & x < \varphi(p)\\2^{x\bmod\varphi(p)+\varphi(p)}&x\ge\varphi(p)\end{matrix}\right.\pmod p \]

很显然 \(x\) 特别大，所以：

\[2^x \equiv 2^{x \bmod \varphi(p) + \varphi(p)} \pmod p \]

即：

\[f(p) = 2^{f(\varphi(p)) + \varphi(p)} \]

可以发现 \(\varphi(p) < p\)，所以上式暴力递归的复杂度是与 \(p\) 同阶的。

边界显然 \(f(1) = 0\)。

$\color{blue}\text{Code}$

int fpm(int a, int b, int P) {
	int res = 1;
	while (b) {
		if (b & 1) res = (ll)res * a % P;
		b >>= 1, a = (ll)a * a % P;
	}
	return res;
}

int p[N], cnt, phi[N];
bool st[N];

void init(int n) {
	phi[1] = 1;
	for (int i = 2; i <= n; ++ i ) {
		if (!st[i]) phi[i] = i - 1, p[ ++ cnt] = i;
		for (int j = 1; p[j] <= n / i; ++ j ) {
			st[p[j] * i] = true;
			if (i % p[j] == 0) {
				// p[j] 是 i 的最小质因子
				phi[p[j] * i] = phi[i] * p[j];
				break;
			}
			phi[p[j] * i] = phi[i] * (p[j] - 1);
		}
	}
}

int solve(int p) {
	if (p == 1) return 0;
	return fpm(2, solve(phi[p]) + phi[p], p);
}

void Luogu_UID_748509() {
	int x;
	fin >> x;
	fout << solve(x) << '\n';
}

\(\color{#FFC116}(4)\) P1313 [NOIP2011 提高组] 计算系数

• 给定一个多项式 \((ax+by)^k\)，请求出多项式展开后 \(x^n\times y^m\) 项的系数。
• \(k \le 10^3\)，\(n + m = k\)，\(a, b \le 10^6\)。

首先视 \(x_0 = ax,y_0=by\)，那么原式可以用二项式定理展开：

\[(x_0+y_0)^k = \sum_{i=0}^k \dbinom ki\times x_0^i \times y_0^{k-i} \]

显然 \(x_0^n \times y_0^m\) 的系数为 \(\dbinom kn\)。

因为 \(x_0^n = (ax)^n = a^nx^n,y_0^m = (by)^m = b^my^m\)，所以 \(x^n \times y^m\) 的系数为 \(\dbinom kn \times a^n \times b^m\)。

$\color{blue}\text{Code}$

int a, b, k, n, m;

int fpm(int a, int b) {
	int res = 1;
	while (b) {
		if (b & 1) res = (ll)res * a % P;
		b >>= 1, a = (ll)a * a % P;
	}
	return res;
}

int C(int a, int b) {
	int res = 1;
	for (int i = a - b + 1; i <= a; ++ i ) res = res * i % P;
	for (int i = 1; i <= b; ++ i ) res = res * fpm(i, P - 2) % P;
	return res;
}

void Luogu_UID_748509() {
	fin >> a >> b >> k >> n >> m;
	fout << C(k, n) * fpm(a, n) % P * fpm(b, m) % P << '\n';
}

\(\color{#BFBFBF}(5)\) 51Nod - 1642 区间欧拉函数

• 给定 \(n\) 个数 \(a_i\)。\(q\) 次查询 \(\varphi (\prod_{i = l}^r a_i) \bmod (10^9 + 7)\)。
• \(n,q \le 2 \times 10^5\)，\(a_i \le 10^6\)。

对于 \(\varphi (n)\) 的求解，首先将 \(n\) 质因数分解为 \(\prod p_i^{c_i}\)，那么 \(\varphi(n) = n \times \prod (1 - \frac 1{p_i})\)。也就是说求解 \(\varphi(n)\) 只需要知晓 \(n\) 的质因子，而并不需要知晓 \(n\) 的质因子的出现次数。

同理，对于 \(\varphi(\prod a_i)\) 的求解，我们需要求出 \(\prod a_i\) 的质因数，也即每个 \(a_i\) 的质因数的并。

回到题目。仿照 HH 的项链 的思路，我们可以将 \(q\) 次询问离线并按照右端点排序。将每个质数的权值定义为 \(1 - \frac 1p\)，然后用线段树求解区间权值乘积，基本就解决了。

$\color{blue}\text{Code}$

int n, q, a[N];

struct Query {
	int l, r, id;
	bool operator <(const Query &h) const {
		return r == h.r ? l < h.l : r < h.r;
	}
}que[N];

int res[N];

int fpm(int a, int b) {
	int res = 1;
	while (b) {
		if (b & 1) res = (ll)res * a % P;
		b >>= 1, a = (ll)a * a % P;
	}
	return res;
}

int calc(int p) {
	return (ll)(p - 1) * fpm(p, P - 2) % P;
}

struct Segment_Tree {
	struct Node {
		int l, r, v;
	}tr[N << 2];
	
	void pushup(int u) {
		tr[u].v = (ll)tr[u << 1].v * tr[u << 1 | 1].v % P;
	}
	
	void build(int u, int l, int r, bool op) {
		tr[u] = {l, r};
		if (l == r) tr[u].v = op ? 1ll : a[l] % P;
		else {
			int mid = l + r >> 1;
			build(u << 1, l, mid, op), build(u << 1 | 1, mid + 1, r, op);
			pushup(u);
		}
	}
	
	void modify(int u, int x, int d) {
		if (tr[u].l == tr[u].r) tr[u].v = d;
		else {
			int mid = tr[u].l + tr[u].r >> 1;
			if (x <= mid) modify(u << 1, x, d);
			else modify(u << 1 | 1, x, d);
			pushup(u);
		}
	}
	
	int query(int u, int l, int r) {
		if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;
		int mid = tr[u].l + tr[u].r >> 1, res = 1;
		if (l <= mid) res = query(u << 1, l, r);
		if (r > mid) res = (ll)res * query(u << 1 | 1, l, r) % P;
		return res;
	}
	
	void modify(int x, int d) {
		int t = query(1, x, x);
		if (d > 0) modify(1, x, (ll)t * d % P);
		else modify(1, x, (ll)t * fpm(-d, P - 2) % P);
	}
	
	int query(int l, int r) {
		return query(1, l, r);
	}
}A, B;

vector<int> primes(int x) {
	vector<int> res;
	for (int j = 2; j <= x / j; ++ j )
		if (x % j == 0) {
			res.push_back(j);
			while (x % j == 0) x /= j;
		}
	if (x > 1) res.push_back(x);
	return res;
}

int lst[M];

void Luogu_UID_748509() {
	fin >> n;
	for (int i = 1; i <= n; ++ i ) fin >> a[i];
	
	A.build(1, 1, n, 0), B.build(1, 1, n, 1);
	
	fin >> q;
	for (int i = 1; i <= q; ++ i ) {
		fin >> que[i].l >> que[i].r;
		que[i].id = i;
		res[i] = A.query(que[i].l, que[i].r);
	}
	sort(que + 1, que + q + 1);
	
	for (int i = 1, j = 1; i <= q; ++ i ) {
		for (; j <= que[i].r; ++ j ) {
			auto v = primes(a[j]);
			for (int p : v) {
				if (lst[p]) B.modify(lst[p], -calc(p));
				lst[p] = j;
				B.modify(j, calc(p));
			}
		}
		
		res[que[i].id] = (ll)res[que[i].id] * B.query(que[i].l, que[i].r) % P;
	}
	
	for (int i = 1; i <= q; ++ i ) fout << res[i] << '\n';
	return;
}

\(\color{#3498D8}(6)\) CF616E Sum of Remainders

• 给定 \(n, m\)，求 \((\sum_{i=1}^m n \bmod i) \bmod (10^9 + 7)\)。
• \(n, m \le 10^{13}\)。

首先根据取模的定义可知 \(a \bmod b = a - \lfloor \frac ab \rfloor \times b\)，那么：

\[\begin{align*}\sum_{i=1}^m n \bmod i &= \sum_{i=1}^m \left(n- \left \lfloor \frac ni \right \rfloor \times i\right)\\ &= n\times m - \sum _{i=1}^m \left(\left\lfloor \frac ni \right\rfloor \times i \right)\end{align*} \]

然后发现 \(\sum _{i=1}^m \left(\left\lfloor \frac ni \right\rfloor \times i \right)\) 是一个整除分块的形式。然后做完了。

注意当 \(i > n\) 时是无贡献的，所以只需要枚举到 \(\min(n, m)\) 即可。

$\color{blue}\text{Code}$

int n, m, res;

int mod(int x) {
	return x % P;
}

int calc(int l, int r) {
	return mod(l + r) * mod(r - l + 1) % P * 500000004ll % P;
}

void Luogu_UID_748509() {
	fin >> n >> m;
	int res = mod(n) * mod(m) % P;
	for (int l = 1, r; l <= min(n, m); l = r + 1) {
		r = min(n / (n / l), m);
		// cout << l << ' ' << r << ' ' << (n / l) % P << ' ' << (r - l + 1) % P << '\n';
		res = ((res - mod(n / l) * calc(l, r) % P) % P + P) % P;
	}
	fout << res;
}

\(\color{#3498D8}(7)\) P2398 GCD SUM

• 求 \(\sum\limits_{i=1}^n \sum\limits_{j=1}^n \gcd(i, j)\)。
• \(n \le 10^5\)。

推式子。

\[\begin{aligned} \sum_{i=1}^n \sum_{j=1}^n \gcd(i, j) &= \sum_{i=1}^n \sum_{j=1}^n \sum_{d \mid \gcd(i, j)}\varphi(d) \\ &= \sum_{i=1}^n \sum_{j=1}^n \sum_{d \mid i 且 d \mid j}\varphi(d) \\ &= \sum_{d=1}^n \varphi(d) \left\lfloor\dfrac nd\right\rfloor^2 \end{aligned} \]

线性筛 \(\varphi\) 即可。

$\color{blue}\text{Code}$

int p[N];		// p[i] 表示第 i 个质数
bool st[N];		// st[i] 表示 i 是否是质数
int phi[N];		// phi[i] 表示 φ(i) 的值
int cnt;

void prime(int n)
{
	phi[1] = 1;
	for (int i = 2; i <= n; i ++ )
	{
		if (!phi[i]) p[ ++ cnt] = i, phi[i] = i - 1;
		for (int j = 1; j <= cnt && p[j] <= n / i; j ++ )
		{
			if (i % p[j]) phi[i * p[j]] = phi[i] * phi[p[j]];		// p[j] 不是 i 的最小质因子 
			else 	// p[j] 是 i 的最小质因子 
			{
				phi[i * p[j]] = phi[i] * (p[j]);
				break;
			}
		}
	}
}

void Luogu_UID_748509() {
	int n; fin >> n;
	prime(n);
	int res = 0;
	for (int i = 1; i <= n; ++ i ) res += phi[i] * (n / i) * (n / i);
	fout << res;
}