24/04/27 图论及 dfs 序相关
\(\color{green}(1)\) CF721C Journey
- 给定一张 \(n\) 个点 \(m\) 条边的有向无环图,边有边权。构造一条 \(1 \to n\) 的路径使得其边权和 \(\le k\) 且经过的点数最多。
- \(n, m \le 5 \times 10^3\),\(k \le 10^9\)。
最简单的想法是设状态 \(f_{i, j}\) 表示 \(1 \to i\) 的边权和 \(\le j\) 的路径的最多点数。那么答案为 \(f_{n, k}\)。
显然状态数会爆炸。参照 AT_dp_e 的思路,我们将状态和值交换,即重新令 \(f_{i, j}\) 表示 \(1 \to i\) 的路径上经过了 \(j\) 个点的最小边权和。剩下的就是平凡的转移了。
一些细节:
- 对于那些没法从 \(1\) 到达的点,我们是不需要考虑它们的。因此我们将剩下的点建一张新图,那么这张图中拓扑排序的起点只有一个——\(1\) 点。
- 对于输出方案,按照一般的套路,维护每个 DP 状态是由哪里转移而来即可。
$\color{blue}\text{Code}$
int n, m, k;
int f[N][N]; // f[i][j] : 从 1 --> i 不超过经过 j 个点的最短路径
int pre[N][N];
bool st[N];
struct Gragh {
int d[N];
vector<pair<int, int> > g[N];
void add(int a, int b, int c) {
g[a].emplace_back(b, c);
++ d[b];
}
vector<pair<int, int> > operator [](int u) {
return g[u];
}
}G1, G2;
void dfs(int u) {
if (st[u]) return;
st[u] = true;
for (auto v : G1[u]) dfs(v.first);
}
void Luogu_UID_748509() {
fin >> n >> m >> k;
while (m -- ) {
int a, b, c;
fin >> a >> b >> c;
G1.add(a, b, c);
}
dfs(1);
for (int u = 1; u <= n; ++ u )
if (st[u])
for (auto t : G1[u]) {
int v = t.first, w = t.second;
if (st[v]) G2.add(u, v, w);
}
queue<int> q;
q.push(1);
memset(f, 0x3f, sizeof f);
f[1][1] = 0;
int cnt = 0;
while (q.size()) {
int u = q.front();
q.pop();
for (auto t : G2[u]) {
int v = t.first, w = t.second;
for (int i = 1; i <= n; ++ i ) {
ll x = f[u][i - 1] + w;
if (x > k) continue;
if (x < f[v][i]) {
f[v][i] = f[u][i - 1] + w;
pre[v][i] = u;
}
}
if (!( -- G2.d[v])) q.push(v);
}
}
for (int i = n; i; -- i )
if (f[n][i] <= k) {
cout << i << '\n';
int x = n, y = i;
stack<int> res;
while (y) {
res.push(x);
x = pre[x][y -- ];
}
while (res.size()) fout << res.top() << ' ', res.pop(); puts("");
return;
}
}
\(\color{green} (2)\) CF731C Socks
- 你有 \(n\) 只袜子,共有 \(k\) 种颜色,有 \(m\) 天。每只袜子有它的初始颜色。在第 \(i\) 天,你会穿第 \(l_i\) 只和第 \(r_i\) 只袜子。求最少改变多少袜子的颜色,使得你每天穿的两只袜子颜色相同。
- \(n, k, m \le 2 \times 10^5\)。
将 \(l_i, r_i\) 连边,会形成若干个连通块。显然每个连通块内的袜子颜色应该是相同的。
对于每个连通块独立考虑。我们希望将这个连通块内的颜色统一,且操作次数最少,最直观的想法就是全部染成出现次数最多的颜色。
令连通块大小为 \(s\),最多的颜色出现了 \(t\) 次,那么答案即 \(\sum (s - t)\)。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, m, k, c[N];
int p[N];
int fifa(int a) {
return a == p[a] ? a : p[a] = fifa(p[a]);
}
map<int, int> mp[N];
int mx[N], cnt[N], res;
int main() {
cin >> n >> m >> k;
for (int i = 1; i <= n; ++ i ) cin >> c[i], p[i] = i;
for (int i = 1, u, v; i <= m; ++ i ) {
cin >> u >> v;
p[fifa(u)] = fifa(v);
}
set<int> S;
for (int i = 1; i <= n; ++ i ) {
int f = fifa(i);
S.insert(f);
mx[f] = max(mx[f], ++ mp[f][c[i]]);
++ cnt[f];
}
for (int i : S) res += cnt[i] - mx[i];
cout << res;
return 0;
}
\(\color{green}(3)\) CF412D Giving Awards
- 请你构造 \(1 \sim n\) 排列 \(P\),满足给定的 \(m\) 条形如 \((u, v)\) 的限制,表示不存在 \(P_i = u\) 且 \(P_{i + 1} = v\)。保证不存在两个限制 \(\mathbf{(u, v)}\) 和 \(\mathbf{(v, u)}\)。
- \(n \le 3 \times 10^4\),\(m \le 10^5\)。
连 \(u \to v\) 的有向边,然后 dfs 整张图。在 \(u\) 的出边全部访问结束后,将 \(u\) 加入答案队列的队尾。
考虑证明这种构造一定是正确的。可以画出一颗 dfs 树,分析三种边的合法性:
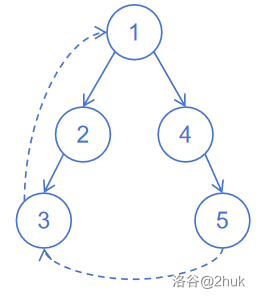
- 树边,例如 \(4 \to 5\)。根据我们的做法,\(4\) 一定在 \(5\) 之后访问。这样是合法的。
- 返祖边,例如 \(3 \to 1\)。由于题目保证「不存在两个限制 \((u, v)\) 和 \((v, u)\)」,所以这条返祖边一定不是指向它的父亲,而是跨越至少一个点。这意味着尽管有 \(3 \to 1\) 这条边,但由于 \(1\) 是祖先,所以它已经在前面被访问过,再次访问到 \(3\) 时它们之间已经隔着若干个点了(例如图中的 \(2\))。所以这样是合法的。
- 横叉边,例如 \(5 \to 3\)。同样的思路,在树上 \(3, 5\) 一定不是直接相连的,而是隔着几个点。这样也是合法的。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, m;
vector<int> g[N];
bool st[N];
void dfs(int u) {
if (st[u]) return;
st[u] = true;
for (int v : g[u]) dfs(v);
cout << u << ' ';
}
int main() {
cin >> n >> m;
while (m -- ) {
int a, b;
cin >> a >> b;
g[a].push_back(b);
}
for (int i = 1; i <= n; ++ i ) dfs(i);
return 0;
}
\(\color{blue} (4)\) CF118E Bertown roads
- 给定一张 \(n\) 个节点 \(m\) 条边的无向联通图。构造一种为每条边都确定一个方向的方案,使得这张图成为一个 scc。或报告无解。
- \(n \le 10^5\),\(m \le 3 \times 10^5\)。
若原图不是一个 dcc,即存在桥,那么一定无解。这是显然的。
否则,我们建一颗 dfs 树,并将树边的方向定为 父亲 \(\to\) 儿子,将返祖边的方向定为 后代 \(\to\) 祖先。显然不存在横叉边。
考虑证明这样做是可行的:
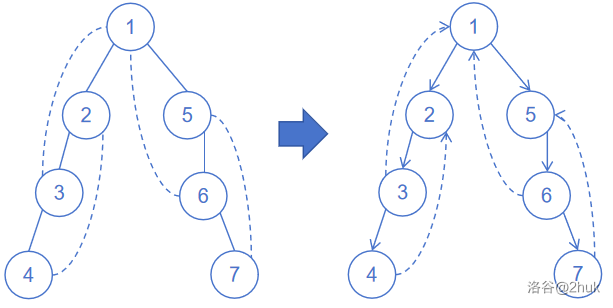
- 由于树边都是向下指,所以祖宗可以到达它的所有后代,包括但不限于祖先可以到达所有节点。
- 对于叶子节点,由于图中不存在桥,所以它一定存在一条返祖边。而这条边指向的祖宗要么为根,要么也存在一条返祖边。以此类推。所以叶子节点总能到达根。然后到达所有节点。
- 对于一般的节点,它可以通过树边到达叶子,再到达根,再到达所有节点。
实现上,我们从 1 开始 dfs。当走到一个已经做过的点时,证明这条边是返祖边,它的真正方向应该是深度深的指向深度浅的。否则若这个点是第一次访问,证明这条边是树边,它的真正方向应该是深度浅的指向深度深的。
所以需要 dfs 预处理出每条树边和返祖边,以及每个点的深度。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
using namespace std;
const int N = 600010;
struct Edge {
int a, b, id;
}edges[N];
int n, m;
vector<pair<int, int> > g[N], tr[N];
bool vis[N], st[N], vise[N];
int w[N], dep[N];
void dfs1(int u, int fa) {
for (auto t : g[u]) {
int v = t.first, id = t.second;
if (fa == v) continue;
if (vise[id]) continue;
vise[id] = true;
if (vis[v]) {
++ w[u], -- w[v];
}
else {
vis[v] = true;
dfs1(v, u);
tr[u].emplace_back(v, id);
st[id] = true;
}
}
}
void dfs2(int u) {
for (auto t : tr[u]) {
int v = t.first;
dep[v] = dep[u] + 1;
dfs2(v);
w[u] += w[v];
}
if (u != 1 && !w[u]) {
puts("0");
exit(0);
}
}
int main() {
cin >> n >> m;
for (int i = 1, u, v; i <= m; ++ i ) {
cin >> u >> v;
edges[i] = {u, v, i};
g[u].emplace_back(v, i), g[v].emplace_back(u, i);
}
vis[1] = true, dep[1] = 1, dfs1(1, -1), dfs2(1);
for (int i = 1; i <= m; ++ i ) {
int u = edges[i].a, v = edges[i].b;
if (st[i]) {
if (dep[u] < dep[v]) swap(u, v);
}
else {
if (dep[v] < dep[u]) swap(u, v);
}
cout << u << ' ' << v << '\n';
}
return 0;
}

