leetcode 540. 有序数组中的单一元素

540. 有序数组中的单一元素

给定一个只包含整数的有序数组，每个元素都会出现两次，唯有一个数只会出现一次，找出这个数。

示例 1:
输入: [1,1,2,3,3,4,4,8,8]
输出: 2

示例 2:
输入: [3,3,7,7,10,11,11]
输出: 10

注意: 您的方案应该在 O(log n)时间复杂度和 O(1)空间复杂度中运行。

          难点在于 O(log n)时间复杂度和 O(1)空间复杂度

方法1 能解决，但是不满足 O(log n)时间复杂度

          主要思路是相同的数异或 ^ 结果为0，那么把数组所有元素都异或一遍，就能得到那个落单的，于0异或不变，与1异或对应位取反

class Solution {
public:
    int singleNonDuplicate(vector<int>& nums) {
        int res=nums[0];
        for(int i =1;i<nums.size();++i){
            res = res^nums[i];
        }
        return res;
    }
};

          补充一种思路：python可以用去重数组的和乘以2减去原始数组和得到结果，且这个方法不要求数组有序，当然放在这个题目下肯定时间复杂度不行

sum(set(nums))*2-sum(nums)

方法2 满足题目的复杂度要求

          二分法，大概含义就是我把数组拦腰分成两段，因为数组是有序的，那么相同的两个数必定是挨着的，我们再分情况想想，

         
1、前面有偶数个数字，那么要么前面一段 [0-mid] 最后两个是成对出现的相同

          要么就是那个落单的在前面，让前面出现两个落单的

2、前面有奇数个数字，那么要么前面一段 [0-mid] 的最后一个和后面一段 [mid+1-nums.length] 的第一个相同

          要么就是那个落单的在前面，

class Solution {
public:
    int singleNonDuplicate(vector<int>& nums) {
        int left = 0, right = nums.size() - 1, mid=0;
        while (left < right) {
            mid = left+(right-left) /2;
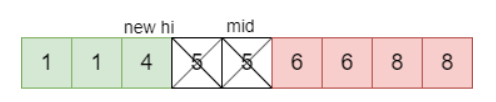
            //巧妙之处，如果mid是奇数，那么[0-mid]之间就有偶数个数字，我只要和前面一个比，相等那么落单的就一定在后面（这儿自己写一个序列，二分来看你就明白了），不等，那落单的一定在前面
            //同理，要是mid是偶数呢，那么[0-mid]之间就有奇数数个数字，我只要和后面一个比，相等那么落单的也一定在后面，不等，那落单的一定在前面
            if (nums[mid] == nums[mid ^ 1]){     
                left = mid+ 1;
            } else {
                right = mid;
            }
        }
        return nums[left];
    }
};